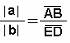Dalle forme naturali ai modelli
Percorso didattico della classe 4D 2001/02 dell'ISA Sperimentale di Monza
Docenti: M. Alati (Morfologia), L. Curcio (Matematica), R. Di Martino (Discipline Geometriche), L. Gerosa (Laboratorio di Comunicazione Visiva), C. Tresoldi (Laboratorio di Arti Applicate).
“...Una piccola raccolta di oggetti curiosi, celebrazione di forme naturali e artificiali, decorava una mensola a parete. Qualche ingegnoso puzzle di legno, qualche sasso sagomato e colorato, delle sfere di cristallo di rocca, qualche turbine sagomato e levigato di conchiglia che rappresenta per ogni occhio quasi l'origine naturale dell'architettura come un tempo ogni fossile era considerato uno “scherzo di natura” e come tale testimone inanimato della creazione del mondo”
(Manlio Brusatin, descrive la casa di Carlo Scarpa nel saggio “la casa dell'architetto” [1])
In questa descrizione molti ritroveranno il proprio piacere di allineare oggetti dalla forma interessante, piccoli appunti visivi di cui tenere conto, per chissà quali percorsi futuri. Chi si occupa di progettazione conosce l'importanza dell'educazione silenziosa che queste forme ci offrono.
Il percorso didattico di cui tratteremo si propone, in qualche modo, come una riflessione su questi temi. È un viaggio guidato nel mondo della forma delle conchiglie, condotto all'interno della didattica di una scuola di design. La finalità primaria di questo lavoro è quella di proporre agli studenti metodi di lettura a carattere prevalentemente scientifico.
Le forme materiali del mondo ci parlano con un linguaggio che è una rete di stimoli simultanei, lontano da quella sequenzialità logica che ci aiuta ad assegnare nomi alle cose e razionalizzare. È un processo in cui le impressioni sensoriali prima vanno estratte dal continuum e poi ordinate in percorsi fatti di domande e tentativi di risposta. Trattenere qualcosa di non occasionale da questo flusso di informazioni è una conquista faticosa ma è uno dei principali obiettivi di una formazione al mondo della visione e del progetto. Svolgendo queste considerazioni in ambito didattico potremmo dire che ogni disciplina possiede filtri di analisi che cercano di tradurre la “continua” realtà in un insieme “discreto” di strutture interpretative.
Gli oggetti naturali, data la straordinaria stratificazione di significati che recano, si prestano egregiamente a indagini, come questa, di carattere interdisciplinare. La spontanea bellezza delle forme naturali inoltre è un traguardo cui tendere; tale bellezza nasce da un'intima relazione tra forma, materiali e funzioni dove ogni spessore, ogni colore appaiono necessari, una sobrietà fatta di infinite sottigliezze, ciò che i teorici del design individuano nella fondamentale categoria della coerenza formale.
L'osservazione delle forme naturali da sempre ha ispirato le scelte progettuali in architettura; dal tema classico della scala a chiocciola, declinato in innumerevoli esempi antichi e contemporanei - dalla mirabile scala del castello di Blois attribuita a Leonardo a quelle di Gaudi per la Sagrada Familia fino al recente museo di Pei a Berlino - a legami più sottili e profondi tra forma architettonica e principio naturale (basti pensare a tutta la tarda produzione di Gaudi fondata su un vocabolario di forme statiche spontanee implicitamente evocanti oggetti naturali). Questo tipo di ricerca, fondendosi sempre più, nel corso del novecento con la cosiddetta architettura degli ingegneri, è stata portata avanti, seppur con linguaggi e approcci molto diversi, da personaggi come Nervi, Musmeci, Le Ricolais, Candela, Buckminster Fuller e Calatrava. Una citazione a parte merita il tedesco Frei Otto fondatore di gruppi interdisciplinari di ricerca ove architetti e ingegneri lavorano a fianco dei biologi. Su un versante di ricerca sicuramente meno ingegneristico sulle forme naturali in architettura - ma non per questo meno interessante - ricordiamo il lavoro di Frank O'Gehry o degli svizzeri Herzog e De Meuron con la loro Natural History.
Struttura del lavoro
La prima parte del lavoro vuole rispondere alle domande: chi produce le conchiglie? a quali funzioni rispondono? La seconda parte si occupa delle proprietà geometrico-matematiche di queste forme e di come sia possibile descrivere la grande varietà visibile in termini di poche variabili. La terza parte, vuole essere una sintesi progettuale: una possibile interpretazione in forma geometrica delle osservazioni condotte nelle prime due fasi, la costruzione di moduli che nelle due e nelle tre dimensioni siano capaci di riprodurre efficacemente le dinamiche osservabili in natura. Nella prima fase è stato determinante l'apporto delle scienze naturali che in termini progettuali ha fornito quelli che si definiscono i criteri informatori del progetto. Nella seconda fase hanno avuto spazio le discipline che studiano la forma in senso più astratto: matematica e geometria descrittiva. Nella fase di progettazione e realizzazione infine, i laboratori di design hanno fornito gli strumenti teorici e tecnici per estrarre dai concetti forme efficaci.
La scelta di questo specifico argomento oltre che dal desiderio di creare forme interessanti è stata dettata fondamentalmente dai seguenti motivi:
1) La didascalica precisione con cui le forme delle conchiglie si prestano ad illustrare un processo facilmente descrivibile in termini geometrico-matematici ma in grado di generare una varietà di forme tanto grande da non apparire come frutto di un unica matrice.
2) Quello delle conchiglie è un caso in cui necessità geometrico-spaziali (in questo caso dettate dalla necessità della crescita isometrica) impongono alla natura le regole del gioco.
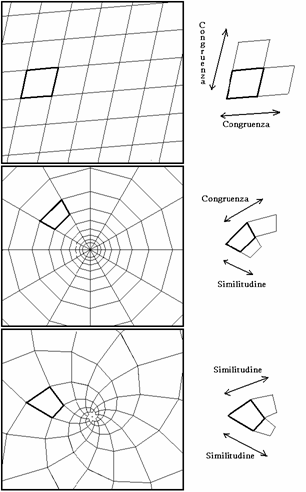
3) La diversa luce che questo percorso getta sulla modularità, uno degli strumenti tradizionali del design. L'analisi condotta attraverso quelli che abbiamo definiti modello 2D e 3D ci dimostra come il tradizionale concetto di modularità basato sulla congruenza delle parti possa essere, in alcuni casi, vantaggiosamente ampliato attraverso il ricorso ad altre trasformazioni geometriche.
Va aggiunto che l'approccio di tipo locale che questo lavoro implica avrebbe potuto essere un'introduzione concreta allo studio dei sistemi complessi. Questa visione ribalta il concetto gerarchico di organizzazione della forma, introducendo i concetti di parallelismo e sensibilità che da anni sono patrimonio delle discipline scientifiche più astratte ma che devono ancora essere conosciute e digerite nell'ambito delle scuole di design (a questo saranno dedicati alcuni progetti didattici dei prossimi anni).
Rapporto forma funzione
Questa parte ampiamente trattata dall'insegnante di scienze naturali è qui ridotta a poche, schematiche, notazioni di carattere funzionale, non essendo possibile per motivi di spazio un maggiore approfondimento. Le scienze naturali studiando le relazioni tra comportamento, ambiente e strategie di sopravvivenza svolgono, dal nostro punto di vista, il ruolo di autentica analisi dei criteri informatori del “progetto conchiglia” quali sono cioè i bisogni a cui deve rispondere.
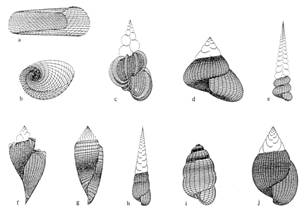
Fig.1 Forme di alcune conchiglie di gasteropodi simulate al computer da Cortie[4]. Tutte queste forme rispondono in diversi contesti alla funzione di scudo portatile.
Schematicamente potremmo osservare che in tutti i casi la conchiglia svolge una funzione di scudo e sostegno delle parti molli anche se i comportamenti delle diverse classi di molluschi sono piuttosto differenziate. Vi sono essenzialmente due tipologie: gusci univalvi e gusci bivalvi. Consideriamo le classi del sottotipo dei molluschi conchiferi:
i Gasteropodi , che sono erbivori o carnivori necessitano, di un guscio portatile che permetta loro spostamenti agevoli in cerca di cibo.
I Gasteropodi presentano la classica conchiglia univalve con avvolgimento più o meno marcato (vedi fig 1).
I Bivalvi sono filtratori stanziali che vivono in ambienti fangosi e si proteggono dai predatori infossandosi velocemente nel fango (vedi fig. 2) grazie alla forma a cuneo della conchiglia composta di due parti (valve) incernierate. La conchiglia bivalve inoltre consente una migliore protezione delle parti molli del corpo dall'azione abrasiva dei granelli di sabbia.
Fig.2 Sequenza dell'infossamento di un bivalve nel substrato fangoso. La conchiglia a cuneo consente una grande facilità di manovra[5].
I Cefalopodi sono predatori che trovano nella velocità di spostamento un'essenziale arma di sopravvivenza hanno per lo più perso la conchiglia esterna conservandone in alcuni casi residui interni con funzioni portanti come per le seppie o i calamari o come organi che favoriscono l'equilibrio idrostatico come per la Spirula. Vi sono delle eccezioni come quella del Nautilus che produce una bellissima conchiglia esterna con funzione di stabilizzatore idrostatico o come l'Argonauta (fig. 3b) che produce tra i tentacoli una delicata struttura esterna, temporanea che utilizza come ovopositore.
a) vediamo la tipica conchiglia a tubo di uno Scafopode (Dentalium) che risponde alla funzione di riparo per un organismo filtratore, stanziale.
b) una conchiglia di Cefalopode Argonauta Argo costruita periodicamente come ovopositore.
La rassegna delle diverse funzioni assegnate alla conchiglia dalle diverse specie di molluschi ci fa pensare a quanto detto da Jacob nel suo “Evoluzione e bricolage”. Egli osserva che, dal punto di vista di un progettista umano, la natura sembra adottare a volte un approccio da ingegnere che concepisce strutture razionalmente pensate per rispondere alle richieste anche estreme dell'ecosistema in cui dovranno operare. Ma più spesso la natura sembra agire come farebbe un appassionato di bricolage che si trova a dover riadattare per nuove necessità strutture nate per tutt'altri scopi.
Nel caso delle conchiglie potremmo forse dire che i rifugi portatili sembrano pensati dall'ingegnere mentre il bricoleur li ha riadattati a ovopositori, scheletri interni o addirittura paratie di galleggiamento simili a quelle di un sommergibile.
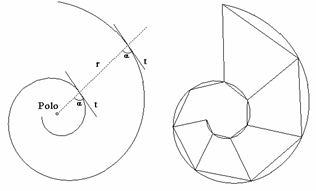
Fig. 4 Nell'immagine a sinistra vediamo una spirale logaritmica su cui è indicato l'angolo a costante tra radiale e tangente che la caratterizza. A destra abbiamo la stessa spirale segmentata in quadrilateri. Immaginando che un ipotetico mollusco abiti nel corso della sua crescita via via il settore più grande, possiamo comprendere come questa strategia abitativa gli consenta di crescere in un guscio rigido senza cambiare forma. Questa strategia nota come crescita isometrica è consentita unicamente da forme strutturate, nel piano e nello spazio, sulla spirale logaritmica. Osservazioni e rilievi morfologici
Le conchiglie di quasi tutti i molluschi, inclusi i bivalvi, sono caratterizzate da un disegno elegante e simmetrico basato su un cono avvolto a spirale lungo un asse.
Da Thompson prendiamo queste osservazioni:
1) crescita per addizione : le conchiglie accrescono le loro dimensioni aggiungendo nuovo materiale a quello preesistente. Pertanto la forma che vediamo conserva e contiene in sé anche tutti gli stadi di crescita precedenti. Ogni conchiglia adulta conserva al suo apice la protoconca da cui ha avuto origine.
2) crescita isometrica : le conchiglie nella loro crescita conservano sempre la medesima forma. Se prendiamo due conchiglie della stessa specie di età diverse ci accorgiamo che le due forme sono l'una l'ingrandimento dell'altra. Questa caratteristica - nota come crescita isometrica - consente al mollusco di aumentare le proprie dimensioni mantenendo immutate le proporzioni tra le parti del corpo contenuto nella conchiglia (vedi fig. 4).È noto sin dal 1638 che la forma a spirale di queste conchiglie possiede la proprietà dell'autosomiglianza durante la crescita (vedi crescita isometrica). Questa proprietà implica che la proiezione di qualsiasi spirale generatrice su un piano ortogonale all'asse di simmetria (in realtà – come verrà spiegato successivamente – è un asse di rototraslazione) produce una curva studiata per la prima volta da Cartesio e da lui definita spirale equiangolare o logaritmica.
Analisi geometrica
Rendiamo più precise le considerazioni sinora svolte citando da Cortie una definizione geometrica dei caratteri morfologici del guscio di una conchiglia. Senza addentrarci nei dettagli del suo modello matematico a 16 variabili ci limiteremo alla sua efficace descrizione dei caratteri fondamentali .
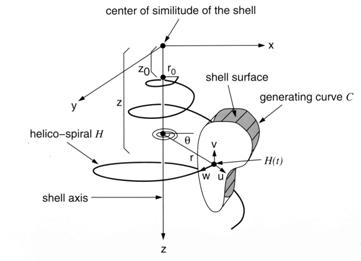
Per semplicità immaginiamo la superficie della conchiglia come il risultato della rotazione di una figura piana (una curva direttrice che rappresenta la forma dell'apertura da cui il mollusco fuoriesce) attorno ad un asse (vedi fig. 5) secondo le seguenti modalità:
Fig. 5 generazione dell'elicospirale per rototraslazione della forma dell'apertura della conchiglia. Da Meinhard (op. cit. Nota 6).
1) Consideriamo un piano “di riferimento” che contiene l'asse di rotazione; la figura direttrice (che immaginiamo piana) può appartenere a tale piano oppure formare con questo un angolo sempre costante.
2) La direttrice, nel corso della rotazione, aumenta in modo costante le proprie dimensioni lineari mantenendo invariate quelle angolari. Ad ogni giro successivo la figura cresce in modo uniforme cioè il tasso di accrescimento della direttrice è costante. Anche la distanza tra la direttrice e l'asse di rotazione si incrementa secondo il tasso di crescita appena citato.
3) La figura nel corso della rotazione, può compiere contestualmente un movimento traslatorio lungo l'asse. Il vettore che descrive l'eventuale traslazione è direttamente proporzionale al tasso di accrescimento della direttrice.
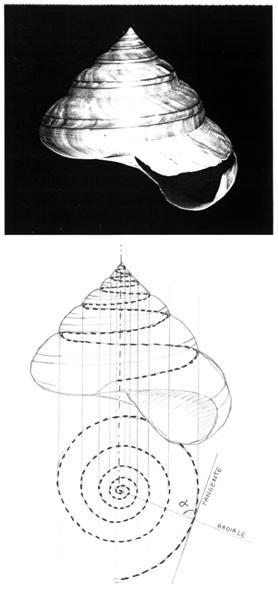
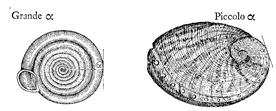
Fig.6 Da una conchiglia (in questo caso una Pleurotomaria) si ricava per proiezione la spirale logaritmica corrispondente. La linea di sutura (tratteggiata) è proiettata da un fascio di rette parallele su di un piano ortogonale all'asse della conchiglia. Dalla spirale proiettata si ricava il valore dell'angolo a che la caratterizza.
Di fianco vediamo da Thompson [7] due conchiglie caratterizzate da diversi valori di α. Nel nostro modello 3Dα si chiamerà il parametro A
Il rispetto di queste condizioni produce un solido (che da ora in avanti chiameremo guscio ) avente come direttrice la forma dell'apertura e come generatrici delle elicospirali che proiettate su di un piano ortogonale all'asse producono, come già accennato, spirali logaritmiche o equiangolari (fig.6 ).
A questo punto l'insegnante di matematica – che ha già introdotto la misura in radianti degli angoli e la rappresentazione dei punti attraverso le coordinate polari – completa l'indagine introducendo la descrizione e l‘equazione della spirale (sia archimedea sia logaritmica).
Dalle descrizioni precedenti prende spunto il nostro lavoro. Le affermazioni appena citate implicano un principio che sarà il cardine della nostra ricerca:
La forma complessa dell'elicospirale può essere suddivisa in parti elementari tra loro simili che indicheremo come moduli .
pertanto:
variando la forma del modulo si modifica la forma dell'elicospirale.
Questa considerazione implica l'assunzione di un approccio di tipo locale. Come avviene in alcuni ambiti della scienza della complessità, noi descriveremo la forma globale solo occupandoci delle relazioni di un modulo con i suoi adiacenti.
Per chiarire questo tipo di approccio ci sembra opportuno partire dallo studio di una situazione più accessibile in termini intuitivi di quella tridimensionale. Ci occuperemo di quello che, forse un po' pomposamente, abbiamo chiamato modello 2D riferito a ipotetiche conchiglie di un mondo in due dimensioni. L'osservazione di questo modello ci aiuterà a comprendere meglio la logica della crescita isometrica che sarà poi il nucleo di un modello 3D che approssima le dinamiche delle forme realmente osservabili.
Il modello 2D
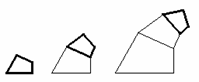
Il modello 2D è uno strumento di grande immediatezza che favorisce un approccio intuitivo al problema della morfogenesi di strutture basate sulla spirale logaritmica. Assumiamo come modulo di partenza un quadrilatero, attraverso una similitudine facciamone una copia ridotta, il tasso di riduzione sarà tale che la misura della base maggiore della copia coinciderà esattamente con quella della base minore della figura di partenza. Collochiamo ora le due figure in modo tale che i due lati in questione siano perfettamente adiacenti. Ripetendo l'operazione un certo numero di volte vedremo crescere una piccola struttura spiraliforme simile a un corno o a una conchiglia (si vedano le figure 8 e 9). In questo paragrafo studieremo i presupposti teorici di questo semplice procedimento e le analogie tra di esso e i meccanismi geometrici di crescita di una conchiglia o di un corno veri.
Fig. 8 Tre momenti dell'aggregazione, in una direzione, di moduli che sono quadrilateri simili a quello marcato.
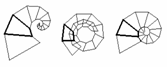
Fig.9 tre aggregazioni lineari prodotte da moduli diversi
Le aggregazioni di quadrilateri
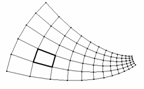
Iniziamo il nostro percorso dall'osservazione che qualsiasi quadrilatero convesso - se aggregato lato a lato con altre sue copie simili - produce una copertura del piano in cui tutti i vertici della pavimentazione appartengono a due distinte famiglie di spirali logaritmiche aventi lo stesso polo ma senso rotatorio opposto. È un procedimento di pavimentazione del piano con moduli tutti della stessa forma ma di diverse misure [nella fig.10 qui sotto abbiamo esempi di come, da un quadrilatero, dato a piacere, si possa sviluppare una copertura del piano].
Fig.10 Aggregazione, in tutte le direzioni di moduli che sono quadrilateri simili a quello marcato:
a) vediamola fase iniziale Il risultato dell'iterazione del processo è una partitura del piano che in base alle caratteristiche del modulo può sviluppare;
b) una pavimentazione (senza sovrapposizioni tra moduli)
b) una pavimentazione (senza sovrapposizioni tra moduli)
Affermiamo pertanto che:
ogni quadrilatero è il modulo di una copertura del piano i cui vertici sono inscrivibili in due famiglie di spirali equiangolari aventi lo stesso polo.
Nel prossimo paragrafo tratteremo in modo sintetico la classificazione di tutti i quadrilateri, per analizzare poi le relazioni che ogni quadrilatero stabilisce con le famiglie di spirali che produce.
La classificazione dei quadrilateri
Abbiamo individuato 4 parametri α β δ e φ, espressi in forma di grandezze angolari, le cui variazioni ci permettono di individuare qualsiasi famiglia di quadrilateri – ottenuti come intersezione di due triangoli - e di distinguere ogni singolo caso possibile (si veda fig.11per una descrizione in termini intuitivi).
In particolare consideriamo come le variazioni dei 4 parametri caratterizzano le categorie dei quadrilateri convessi (ricordiamo, che in questa descrizione, quando un angolo è uguale a 0 le due rette che vi concorrono sono parallele):
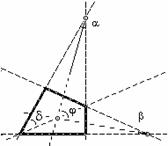
Fig. 11 I quattro parametri che consentono la individuazione di tutti i quadrilateri convessi:
α, β angoli ai vertici dei due triangoli che per sovrapposizione generano il quadrilatero;
φ angolo di intersezione delle bisettrici di α e β. i l vertice di j in genere non giace sulla diagonale;
δ angolo sul vertice “esterno” (quello opposto al polo) del quadrilatero, compreso tra la diagonale in esso incidente e il lato adiacente che concorre ad α.a) con α, β > 0 abbiamo i quadrilateri generici
b) con α=β=0 abbiamo i parallelogrammi,
all'interno di questi:
quando φ=90° abbiamo i rettangoli,
tra i quali quando δ=45° abbiamo il quadrato.
In tutti gli altri casi quando la relazione tra gli angoli δ ed φ è δ=φ/2 allora abbiamo i rombi.
c) con α oppure β=0 abbiamo i trapezi (con φ=90° abbiamo quelli isosceli).
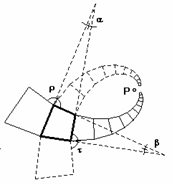
Fig.12 Dai valori degli angoli α e β che caratterizzano un quadrilatero si possono ricavare i valori degli angoli ρ e τche caratterizzano le due famiglie di spezzate spiraliformi che esso produce attraverso la relazione:
ρ=180°-α; τ=180°-β
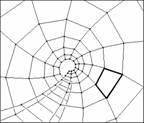
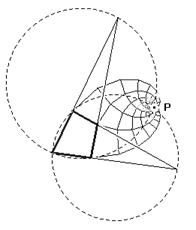
Fig. 13 Dato un quadrilatero si individuano i cerchi circoscritti ai triangoli che, attraverso la loro sovrapposizione, idealmente lo compongono, cioè i due triangoli di vertici a e b che abbiamo utilizzato per la classificazione. L'intersezione dei due cerchi descritti individua due punti: uno è un vertice del quadrilatero, l'altro è il polo del sistema di spirali prodotto da quel quadrilatero.
Quadrilateri e pavimentazioni
Alla luce dei parametri per la classificazione dei quadrilateri riprendiamo il discorso sulle relazioni tra di essi e le coperture che producono. Considerando che “ ad ogni quadrilatero corrisponde una copertura” vediamo le due relazioni fondamentali tra un quadrilatero e la coperture da questo generato:
a) dato un quadrilatero ad esso corrisponderà una copertura del piano formata da due famiglie di spirali equiangolari, aventi lo stesso polo, caratterizzate rispettivamente dai valori angolari: ρ=180°-α; τ=180°-β ;
b) dato un quadrilatero, il polo del sistema di spirali - che formano la copertura che gli corrisponde – è uno dei due punti di intersezione (l'altro è un vertice del quadrilatero) delle due circonferenze circoscritte ai due triangoli che per sovrapposizione creano il quadrilatero (vedi fig.13).
Fig. 14 Pavimentazione prodotte da diverse tipologie di quadrilateri
Rivolgendo le considerazioni sinora svolte alle classi di quadrilateri osserviamo quanto segue (vedi tabella riassuntiva nella fig. 14 qui sopra).
I parallelogrammi , presentando valori α e β uguali a 0, producono sistemi di spirali che sono rette e quindi la copertura corrisponde a una pavimentazione del piano di moduli tra loro congruenti. In questo caso il polo del sistema è da considerarsi infinitamente lontano (un punto all'infinito).
I trapezi, presentando il valore di α (o di β) uguale a 0, producono sistemi di spirali in cui i lati non paralleli di un modulo sono allineati con il polo. Nel caso di trapezi isosceli il sistema di spirali collassa in un sistema di cerchi concentrici e rette radiali passanti per il polo.
I quadrilateri generici, presentando valori α e β diversi da 0, producono - in genere - sistemi di spirali in cui i lati di un modulo non sono mai allineati con il polo.
Pavimentazioni di quadrilateri e conchiglie 2D
Da questa panoramica sulle coperture prodotte da quadrilateri simili veniamo allo scopo di questa sezione che è quello di produrre forme che siano modelli 2D di ipotetiche conchiglie dello spazio a due dimensioni. Da una conchiglia, anche se in 2D, ci aspettiamo, per prima cosa, un avvolgimento serrato cioè che tra una spira e la successiva non vi siano spazi residui o sovrapposizioni. Notiamo che l'avvolgimento serrato è un elemento primario di identità visiva di una conchiglia. Per produrre un modello di conchiglia 2D un quadrilatero deve pavimentare in modo tale che tutta la tassellatura sia il risultato dell'avvolgimento di una sola striscia. Non tratteremo più a fondo un argomento che per essere sviluppato richiederebbe l'uso di strumenti che esulano dalla semplice geometria di base utilizzata in questo lavoro. È interessante notare come questo aspetto del modello 2D ci induca a riflettere sui problemi geometrici legati alla fillotassi aprendo gli orizzonti alla quasicristallografia delle infiorescenze.
Costruzione geometrica di un avvolgimento serrato.
Immaginiamo di voler produrre una conchiglia, cioè un avvolgimento serrato di moduli a partire da un quadrilatero convesso qualsiasi che come vediamo nell'immagine 16a produce un avvolgimento aperto.
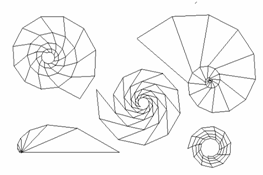
Troviamo per ogni quadrilatero della fila il punto di intersezione delle diagonali e quindi uniamo tra loro i centri dei moduli adiacenti e quelli dei moduli che si trovano l'uno di fronte all'altro nelle spire successive della striscia fig.16b . Una volta individuato un quadrilatero potremo svilupparne una striscia che sicuramente produrrà un avvolgimento serrato o trarne una pavimentazione del piano. Nella fig.17 osserviamo una collezione di conchiglie 2D così prodotte e vediamo che possono essere interpretate come una proiezione su di un piano di conchiglie 3D.
Nel prossimo paragrafo potremo verificare una strettissima analogia di caratteri tra i due sistemi in due e tre dimensioni, quasi una semplice traduzione da 2D a 3D. Ci sembrano particolarmente significative, queste corrispondenze:
nel piano
la struttura è sempre organizzata attorno a un punto, il polo della spirale principale;
i segmenti che rappresentano le basi dei moduli, formano un angolo costante rispetto a un raggio uscente dal polonello spazio
la struttura è sempre organizzata attorno ad una retta l'asse delle elicospirali generatrici;
i poligoni che rappresentano le basi dei moduli formano un angolo costante rispetto ad un piano passante per l'asse di rototraslazione
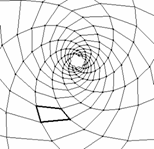
Fig. 17 Tipologie di “conchiglie” prodotte da diversi moduli 2D è evidente la varietà di forme e la somiglianza con immagini di conchiglie vere. Il dato interessante è che questa somiglianza segnala una stretta analogia tra i principi morfologici, non si tratta quindi di copie ma di oggetti prodotti (almeno in termini spaziali) dallo stesso processo.
Questa parte del lavoro è stata resa possibile grazie all'uso di un supporto informatico interattivo come Cabri II. Attraverso la creazione di una macrocostruzione si possono aggregare velocemente i quadrilateri simili di dimensioni opportune. Senza l'uso del computer questo lavoro sarebbe quasi impossibile da gestire graficamente.
Il modello 3D
Il modello 3D si basa su un'idea molto semplice, l'estensione del modello 2D alle tre dimensioni.
Come abbiamo visto, nel piano è sufficiente assemblare copie simili di un quadrilatero per produrre una spirale logaritmica, altrettanto nello spazio è possibile individuare una forma base che aggregata in copie simili produce una elicospirale.
L'idea è quella di collocare nello spazio due poligoni simili (che per semplicità penseremo come regolari) in posizioni arbitrarie e quindi unire con dei segmenti i punti che individueremo come vertici corrispondenti. [Nelle immagini a lato vediamo l'operazione condotta con due esagoni regolari].
L'unico vincolo che poniamo alla libera scelta delle posizioni delle basi nello spazio è quello dell'assenza di rotazione reciproca tra esse. Ciò significa che accostando i piani di appartenenza delle due basi del modulo, (come per chiudere le pagine di un immaginario quaderno) esse ci appaiono come il risultato di un'omotetia.
La figura generata da questa semplice operazione è il modulo [per una descrizione più precisa della sua costruzione vedi colonna a lato].
La costruzione del modulo
1) su di un piano collochiamo un poligono, che costituirà la base inferiore del nostro modulo; la base superiore sarà costituita da un poligono simile al precedente. Posizioniamo arbitrariamente nello spazio la base superiore del modulo scegliendo anche un'inclinazione arbitraria. Comunque porremo le basi nello spazio potremo sempre immaginarle come giacenti su due piani incernierati (come pagine di un quaderno)
2) uniamo tra loro i vertici corrispondenti, cioè quelli che si corrispondono nell'omotetia piana appena citata (AA', BB' nella fig ) fino a formare una figura somigliante ad un tronco di piramide: è il modulo. È dimostrabile che, in genere, i quadrilateri che costituiscono le facce laterali di questa figura non sono piane.
AggregazioneProcediamo nella costruzione del nostro modello 3D eseguendo, attraverso una similitudine, alcune copie del modulo. Il rapporto di questa similitudine sarà quello che intercorre tra le dimensioni delle due basi del modulo. Procedendo in tal modo produrremo una serie di moduli di grandezze decrescenti. I moduli saranno aggregati (uno sopra l'altro) in modo da far coincidere le coppie di basi aventi le stesse dimensioni, avendo cura di far coincidere i vertici corrispondenti Con questo procedimento di aggregazione otterremo una struttura spaziale dall'andamento spiraliforme le cui caratteristiche dipenderanno in tutto dai parametri che controllano la forma del modulo.
Parametri del modulo
A questo punto del lavoro, dopo avere esposto le operazioni base di costruzione e aggregazione vediamo in modo essenziale come - modificando i fattori critici della forma del modulo - si possono riprodurre, in forma essenziale, le dinamiche osservabili in natura.
Si può dimostrare che con qualsiasi scelta dei seguenti parametri si ottiene sempre un modulo in grado di generare per aggregazione un solido inscrivibile in un guscio cioè una superficie avente elicospirali come generatrici :A ) l'inclinazione reciproca tra le basi (valore angolo diedro γ),
B ) il rapporto di omotetia che lega le due basi,
C = AC/AB : DC/DE
C ) il birapporto tra le distanze delle due basi rispettoalla cerniera,
D ) il coefficiente che esprime il valore della reciproca traslazione tra le due basi con vettore parallelo all'asse di rototraslazione,
Il parametro A influenza direttamente la velocità con la quale il nostro guscio si avvolge attorno all'asse. È il parametro a tradizionalmente indicato dai biologi (vedi fig.6)
Il parametro B influenza l'ampiezza del cono che avvolto genera il guscio (immaginando di azzerare il parametro A il nostro guscio sarebbe una cono più o meno appuntito, secondo il valore del parametro B).
Il parametro C invece influenza l'inclinazione delle basi, rispetto all'asse, durante la rototraslazione.
Il parametro D è il vettore che controlla lo spostamento delle due basi in direzione parallela alla cerniera del modulo e quindi all'asse di rototraslazione della struttura. Questo parametro è quello che nella realtà distingue le conchiglie “appuntite”, come quella della Turritella, da quelle “piatte” come il Nautilus o le Ammoniti. Come è facilmente intuibile la differenza è data dalla presenza della traslazione lungo l'asse (molto evidente nel primo caso, praticamente assente nel secondo).
Il parametro D è l'unico non descrivibile in proiezione laterale in quanto indica la componente traslatoria del modulo in direzione parallela all'asse di rototraslazione. In parole più semplici ci dice se esiste uno spostamento laterale nel posizionamento relativo delle due basi del modulo (nella figura è individuato dal vettore a).
Nella figura g) vediamo le basi di due moduli consecutivi collegate alle rispettive cerniere di rotazione da un segmento tratteggiato perpendicolare alla cerniera e passante per i centri delle basi. Le frecce evidenziate (vettori) indicano l'entità delle due traslazioni. tra i vettori di due moduli adiacenti intercorre lo stesso rapporto che esiste tra le due basi di un modulo. Facendo riferimento all'immagine in g) relativa ai due moduli aggregati che vediamo in h) diremo che:
I modelli costruiti
In seguito allo studio effettuato abbiamo realizzato una serie di modelli in metallo e plexiglass che vediamo nelle fotografie di questo paragrafo. L'intento era quello di rappresentare alcune delle categorie più significative del mondo delle conchiglie dei molluschi marini.
Tutti i modelli sono costruiti su di un modulo con basi ottagonali. Allo scopo di ovviare al problema delle facce laterali dei moduli che, come accennato, si presenterebbero curve abbiamo scelto di evitare di realizzarle collegando le basi ottagonali con una struttura continua in metallo. Questa scelta evidenzia la forma della struttura portante basata su una spirale logaritmica piana e consente di sottolineare il ruolo fondamentale di questa forma che detta i ritmi di crescita anche nello spazio.
Questi in realtà sono da considerare modelli di studio in cui abbiamo scelto di affrontare situazioni particolarmente adatte a una rappresentazione schematica.Il lavoro didattico in futuro potrà svilupparsi almeno in due direzioni:
cercare di rappresentare un tipo specifico di conchiglia individuando -attraverso i linguaggi dei diversi ambiti disciplinari - un modulo e una strategia costruttiva appropriati a quel caso;
costruire modelli di conchiglie “impossibili” di particolare bellezza e interesse formale.
Questo rapporto possibile-impossibile è un tema particolarmente stimolante per una ricerca sui fondamenti linguistici come questa ed è uno dei temi specifici di una ricerca condotta con criteri scientifici.
Bibliografia essenziale
[1] Manlio Brusatin “La casa dell'architetto” da: “CARLO SCARPA - opera completa” F. Dal Co, G. Mazzariol Electa Milano 1984
[2] In particolare citiamo il quaderno : “IL 9 - Pneus in nature and technics” [il paragrafo Growt despite hardening, dedicato alle conchiglie]
[3] Peter S.Stevens "LES FORMES DANS LA NATURE" Seuil Evreux 1978
[4] M.Cortie "THE FORM, FUNCTION, AND SYNTESIS OF THE MOLLUSCAN SHELL" da: “SPIRAL SYMMETRY” a cura di I.Hargittay World Scientific 1990
[5] G.Mezzetti "L'UOMO. DALLA NATURA ALLA SCIENZA" La Nuova Italia 1987
[6] Francois Jacob “EVOLUZIONE E BRICOLAGE” Einaudi Torino 1978
[7] D'Arcy W.Thompson "CRESCITA E FORMA" Boringhieri Torino 1961 [prima ed.1917]
[8] H.Meinhardt "THE ALGORITMIC BEAUTY OF SEA SHELLS" Springer Verlag Berlin 1995
[9] Theodore Andrea Cook “The Curves of life” Dover Publications Inc., New York 1978 [prima ed. 1914]
[10] Richard Dawkins “Alla conquista del monte improbabile” (Climbing mount improbable) Mondadori Milano 1997
[11] Robert D.Barnes "ZOOLOGIA: GLI INVERTEBRATI" Piccin Padova 1985