Econofisica - Fondamenti di una nuova scienza
I modelli fisici si stanno rivelando quanto mai adatti per affrontare la complessità dei mercati finanziari. Ma che rapporto ci può essere tra due discipline apparentemente così lontane, come la Fisica e l'Economia? Che cosa ci insegna la storia del pensiero scientifico degli ultimi 100-150 anni? Discutendo le principali applicazioni e le numerose questioni ancora aperte, troviamo un trascurato articolo di Ettore Majorana sull'importanza dei metodi della Meccanica quantistica nel campo delle scienze sociali. Era la fine degli anni '30!
Fisica ed Economia: paradigmi a confronto
“Do we really believe Nature is written in numbers?”
Tom Stoppard, Arcadia
La teoria economico-matematica è nata con l'intento di utilizzare la Matematica come strumento per descrivere quanto accade in Economia e trasformare la scienza economica in una scienza formalizzata. Il pensiero economico ha mostrato un certo spirito d'emulazione verso l'apparato concettuale e gli strumenti utilizzati dalla Fisica. Del resto, questo interesse non deve destare particolare sorpresa poiché nel mondo occidentale le scoperte della Fisica, insieme con i correlati sviluppi tecnologici, hanno costituito il motore del processo di crescita globale.
Più recentemente, l'informatizzazione ha rappresentato un ulteriore incentivo alla collaborazione tra fisici ed economisti. Una più capillare registrazione dei dati relativi agli eventi economici ha, infatti, richiesto un deciso miglioramento nello studio di come circola il denaro.
La registrazione della maggior parte delle transazioni che avvengono sui mercati finanziari sono disponibili ora in forma elettronica e possono essere elaborate con un'estrema accuratezza statistica. Nel caso della Borsa di New York (NYSE), esiste una banca dati che ha registrato tutte le offerte di vendita e d'acquisto dal 1993. Una quantità impressionante di dati finanziari dell'ordine del TeraByte. Questa memorizzazione informatizzata, sempre più capillare, richiede analisi sempre più efficienti.
Cosa c'entra la Fisica con questo? La mancanza di un disordine perfetto nella successione di questi dati non esclude che dietro le scelte umane si celi un ordine ineffabile, il cui complesso segreto non sia rintracciabile semplicemente nella proprietà dei numeri, ma che vada ricercato nella comprensione delle teorie associate a regolarità e simmetrie. Negli ultimi anni, lo sviluppo raggiunto dalla Fisica teorica nello studio di queste proprietà ha alimentato la convinzione che potesse essere impiegata nello studio dei sistemi complessi, siano essi biologici od economici. Non si tratta di un rigurgito di positivismo, ma della concreta potenza predittiva di alcuni metodi matematici legati alla formulazione di sofisticate teorie fisiche.
Sulla base di alcuni principi fisici fondamentali è possibile, infatti, elaborare ben precisi modelli che sono in grado di descrivere alcune caratteristiche generali di un sistema disordinato.
Queste teorie hanno applicazioni in molte aree della Fisica, soprattutto in quelle in cui intervengono probabilità e statistica ed in cui la complessità non permette una formulazione con leggi esatte. L'insieme delle tecniche sviluppate ha naturalmente indotto i fisici ad estendere i propri interessi ed applicare i risultati ad altri sistemi complessi disordinati come ecosistemi, reti neurali o mercati finanziari. Sulla base di queste premesse, fisici ed economisti hanno cominciato ad interagire in maniera più sistematica ed approfondita.
Da quest'interazione è emersa una nuova disciplina: l'Econofisica, un nuovo ramo interdisciplinare che coniuga la Finanza quantitativa e la Matematica finanziaria con i potenti metodi e modelli sviluppati in settori come la Meccanica statistica, la Dinamica non lineare, la Fisica della materia condensata, la Fisica (sub)nucleare delle alte energie e li applica all'analisi dei mercati e dei prodotti finanziari. Non è estranea a questa collaborazione neppure l'Astrofisica, che ha sviluppato diversi modelli cosmologici in Teoria della relatività generale e sofisticate tecniche statistiche per analizzare le asimmetrie della radiazione cosmica e gestire la mappa dinamica del moto degli ammassi stellari.
L'Econofisica non si riduce ad un miglioramento della trattazione di problemi di statistica finanziaria ma aspira ad essere complementare ed originale (nei metodi e nei contenuti) rispetto ai settori disciplinari tradizionali come l'Econometria. Ha così richiamato, dapprima, l'attenzione del mondo accademico e, gradualmente, anche quella delle istituzioni finanziarie. L'interesse e lo studio pianificato di sistemi economici risale per lo meno alla fine degli anni Ottanta, con l'esperimento del Santa Fé Institute for Complex Studies (SFI) nel New Mexico, dove fisici, economisti, biologi e informatici discutevano (e discutono) di sistemi complessi osservandoli e confrontandosi dai rispettivi punti di vista. La crescita del mercato e della competitività ha favorito negli anni ‘90, in particolare negli Stati Uniti ed in Inghilterra, un vasto fenomeno di trasferimento di profili di tipo fisico-matematico provenienti dalla ricerca accademica verso le istituzioni finanziarie. Una statistica della rivista Nature nel 1997, riportava che il 48% dei dottori in ricerca in Fisica erano già impiegati nel settore finanziario. Il fenomeno è giunto anche nel nostro Paese verso la fine degli anni ‘90, ove ha trovato fertile terreno grazie all'ammodernamento e all'internazionalizzazione del settore finanziario indotto dall'entrata in vigore delle nuove norme dell'Unione europea. In Italia, un rapido censimento evidenzia che vi sono diversi gruppi di ricerca interessati all'Econofisica in numerose Università.
Di per sé, il neologismo Econofisica è relativamente recente. Il termine, apparso nel 1995 durante la Conferenza StatPhys di Calcutta, cominciò a diffondersi dopo un Convegno a Budapest nel luglio 1997 (Workshop on Econophysics: An Emerging Science), dedicato esplicitamente all'Econofisica, divenendo familiare nel 2000 con la comparsa del libro di Mantegna e Stanley An Introduction to Econophysics: Correlations and Complexity in Finance. Attualmente, si contano una decina di manuali che hanno come specifico argomento l'Econofisica.
La comunità dei fisici che opera in ambito finanziario continua ad essere in crescita. I motivi di questo fenomeno possono essere ricercati nelle caratteristiche peculiari del bagaglio culturale dei fisici, la naturale propensione alla modellizzazione di problemi complessi, l'orientamento al problem solving, la familiarità nel manipolare grandi quantità di dati e l'abilità nell'utilizzare gli strumenti informatici.
Un'interazione così promettente non è spiegabile senza comprendere che la Fisica è una scienza quantitativa. Spiegare i fenomeni naturali significa, in ultima analisi, poter elaborare previsioni quantitative in accordo con i risultati degli esperimenti. Questa insistenza sulla quantificazione non è un puntiglio, ma una caratteristica fondamentale della Fisica sin dagli inizi, prodiga di successi e causa motrice di un incredibile sviluppo tecnologico.
La convinzione che il paradigma della Fisica potesse essere trasferito in altre discipline, come quelle economiche, incontra comunque numerose difficoltà. L'assenza di principi generali e di una formulazione teorica esauriente degli eventi economici limita fortemente l'influsso della Fisica. Nell'ambito economico si è affermato un criterio empirico, fenomenologico, pragmatico, basato sullo studio dei modelli, piuttosto che su leggi e postulati. Nel caso della distribuzione dei dati dei mercati finanziari, questo approccio sembra adattarsi al seguente schema:
• osservazione dei dati finanziari;
• ricerca di un modello conveniente;
• elaborazione e parametrizzazione del modello per interpolare le osservazioni;
• interpretazione a livello economico dei parametri e dei risultati.
La complessità dei mercati finanziari non sembra suggerire che Economia e Fisica abbiano metodologicamente molti punti in comune, nonostante l'idea di trovare ispirazione per i modelli economici dalle teorie fisiche affondi le proprie radici nel tempo. La letteratura è piena di esempi di famosi fisici con interessi per i problemi economici e finanziari. È esemplare il caso degli sfortunati investimenti di Sir Isaac Newton, che pare abbia perso la spaventosa somma di ventimila sterline investendo nella bolla speculativa del 1720 della South Sea Company in un momento sbagliato in cui le azioni passarono, fra aprile e luglio, da 128 a 1050, per ricadere subito dopo a 175 sterline. “Posso calcolare il moto dei corpi celesti, ma non la pazzia delle folle” ribadì Newton. Più oculata fu la gestione dei fondi delle vedove dell'Università di Gottinga da parte di Carl Friedrich Gauss, la cui consulenza finanziaria lo arricchì non solo di esperienze.
La bellezza e le potenzialità dei Principia Mathematica di Newton furono ben presto inquadrate nel formalismo matematicamente più sofisticato della Meccanica analitica, grazie essenzialmente a Lagrange ed Hamilton.
Tali potenzialità non passarono inosservate nella comunità degli economisti, che cominciarono a considerare la possibilità di adattare lo studio dei sistemi dinamici alle modellizzazioni economiche. L'impatto delle teorie fisiche è ben descritto da Adam Smith, uno dei padri classici dell'Economia che, nel suo libro I principi che guidano e dirigono le ricerche filosofiche, illustrate dalla storia dell'astronomia, esemplifica le analogie concentrandosi sui successi dell'Astronomia e sul ruolo delle regolarità nel formulare modelli (chiamati da Smith “ strumenti immaginari ”) utili per le predizioni nelle scienze sociali.
Economisti del calibro di Walras e Pareto completarono tutto il lavoro necessario per trasferire il formalismo della Meccanica classica nelle strategie per l'analisi finanziaria, in cui i punti materiali si tramutano in eventi economici, l'energia potenziale è rappresentabile dall'utilità economica e l'evoluzione dinamica dei sistemi, sia fisici sia economici, si suppone governata da un principio di minima azione.
Il fascino della Meccanica è stato così intenso per gli economisti che gran parte dei modelli elaborati si sono focalizzati sulla definizione, e le corrispondenze, del concetto di equilibrio e di conservazione in Fisica ed in Economia. Questa attrazione per il determinismo della Meccanica classica è proseguito con successo per tutta la prima metà del XX secolo. Ispirandosi alle leggi di Newton, generazioni di studiosi hanno cercato l'essenza ultima delle teorie economiche, attraverso formulazioni diverse, ciascuna delle quali aspirava al ruolo di verità ultima, valida sempre ed ovunque. La gran mole di studi scaturita da tale approccio ha contribuito ad edificare i fondamenti del pensiero economico. Tuttavia, nessuna formulazione è stata in grado di avvicinarsi al livello di capacità predittiva che caratterizza la legge di gravitazione universale. Tale evenienza non può essere attribuita all'inadeguatezza dell'apparato matematico, il quale peraltro si è dimostrato notevolmente efficace nell'ambito delle discipline concernenti i fenomeni naturali. La scarsità di capacità previsionali, che affligge le scienze sociali, va attribuita a cause assai più profonde e strutturali. È probabilmente opportuno far riferimento ad una filosofia interpretativa dei processi economici che presenta caratteristiche paradigmatiche (nel senso di Kuhn) assai differenti da quelle possedute dall'insieme di modelli, schemi, leggi che si erano sviluppate per interpretare i fenomeni fisici.
Nel confronto tra Meccanica classica ed Economia, possiamo distinguere due paradigmi differenti. Nei due approcci sono diverse non soltanto le tecniche di calcolo o le ipotesi di partenza, ma la concezione stessa di ciò che si intende per previsione o per spiegazione di un fenomeno. In altre parole, sono diverse le scelte di ciò che si assume come dato e di ciò che si intende sottoporre a verifica. I fisici hanno un paradigma fondato sulla convinzione che una teoria deve essere in grado di fornire previsioni quantitative – anche se probabilistiche – dei risultati sperimentali, ricavabili univocamente dalle soluzioni di equazioni dinamiche generali valide per tutti i sistemi fisici. D'altra parte, all'interno della comunità degli economisti, si è affermato un paradigma che accoglie come teoria qualunque contributo che conduca a correlazioni non individuate in precedenza. Dunque, a causa dei problemi pratici da risolvere, gli economisti si accontentano (non potendo far altro) di uno schema interpretativo basato semplicemente sulla (auto)consistenza, pur pretendendo una capacità previsionale quantitativa.
Dal punto di vista fisico, è tuttavia sorprendente come la rivoluzione concettuale, basata sul concetto di probabilità statistica proposto da Boltzman, e soprattutto le teorie quantistiche entrino molto più tardi nell'orizzonte di interesse dell'Economia.
L'unica eccezione è costituita dalla trascurata anticipazione da parte di Louis Bachelier, nella sua tesi di dottorato, dell'analogia tra la dinamica dei prezzi della Borsa di Parigi (con le caratteristiche dei cammini casuali del moto browniano) e tutta la formulazione dei processi markoviani, che precede di cinque anni l'interpretazione di Einstein (nonché di Smoluchowski) sul moto di diffusione casuale. Dal punto di vista concettuale, l'abbandono della visione deterministica di Laplace per un nuovo approccio fondato sulla Meccanica statistica risiede nell'elaborazione di nuove tecniche in grado di analizzare sia sistemi a molti corpi interagenti che più complessi sistemi stocastici.
Negli ultimi decenni, la teoria dei sistemi dinamici ha assunto un ruolo centrale in molti settori della Fisica. Tra le ragioni di questa preminenza vi è stata la progressiva generalità e versatilità di questi nuovi modelli teorici, particolarmente adatti allo studio dei sistemi complessi. La Meccanica statistica ha mostrato con successo che concetti probabilistici permettono di esprimere proprietà molto generali e nel contempo indipendenti dalla natura specifica dei sistemi complessi. Si è così compreso che le proprietà statistiche possono essere efficacemente simulate da modelli puramente stocastici. La teoria della probabilità e dei processi stocastici rappresentano quindi tecniche fondamentali nella formulazione della Meccanica statistica contemporanea. In questo processo di progressiva generalizzazione, lo studio dei sistemi quantistici ha richiesto lo sviluppo di nuovi metodi funzionali e le applicazioni in questo settore hanno acquistato rilievo negli ultimi tempi. Tuttavia manca ancora una comprensione soddisfacente per poter validamente utilizzare tali ricerche nel contesto economico, come anticipava con lungimiranza Ettore Majorana negli anni Trenta del secolo scorso.
Majorana: Fisica quantistica e scienze sociali
“La fisica atomica di cui dovremo principalmente occuparci, nonostante le sue numerose e importanti applicazioni pratiche –e quelle di portata più vasta e forse rivoluzionaria che l'avvenire potrà riservarci- rimane anzitutto una scienza di interesse speculativo, per la profondità della sua indagine che va veramente fino all'ultima radice dei fatti naturali”
Ettore Majorana, Prolusione al Corso di Fisica Teorica, Napoli, 13 gennaio 1938
La possibilità del legame tra la nascente Fisica quantistica e le scienze sociali fu anticipato da Ettore Majorana. La sua è una delle tante storie “maledette” di cui è costellata la storia della Scienza. Esistenze consumate dallo studio, dalla creatività potente e feroce che nasce dal tormento interiore. Vite inquiete che diventano leggende. È anche la storia del disagio esistenziale dei giovani collaboratori che (aspirando al proprio successo) circondavano e si confrontavano con Sua Eccellenza Enrico Fermi, troppo sbrigativamente etichettati indistintamente come la generazione entusiasta dei ragazzi di via Panisperna, dal luogo dove sorgeva a Roma il prestigioso Regio Istituto di Fisica.
Ettore Majorana era uscito relativamente presto da questo gruppo, proprio quando stava accingendosi a scoperte fondamentali sulla composizione del nucleo atomico. Dopo il ritorno dal suo soggiorno di studio in Germania (1933) e la morte del padre (1934), era entrato in una fase di isolamento quasi totale, non trovando nemmeno nel successo accademico una via di uscita dai propri drammi e da quel senso di non appartenenza che affligge i grandi uomini. Majorana, difficilmente catalogabile ed assimilabile ai compagni di studi e soprattutto coscienza inquieta di quella stagione di orgoglio italico e fascista, è stato uno dei più promettenti fisici teorici (non solo italiani) di un'epoca di per sé ricca di ingegni. Pochi mesi prima di scomparire, era stato nominato – non per concorso, ma ‘‘ per l'alta fama di singolare perizia '' – professore ordinario di Fisica teorica nell'Università di Napoli.
Di un uomo simile, Enrico Fermi osò scrivere a Mussolini che lo aveva singolarmente colpito la sua capacità di “svolgere ardite ipotesi e di criticare acutamente (…) calcolatore espertissimo e matematico profondo che mai per altro perde di vista dietro il velo delle cifre e degli algoritmi l'essenza reale del problema fisico ”. Per Fermi, che mai esagerava con i complimenti, Majorana era alla pari con geni come Galilei e Newton.
In questi settanta anni che ci separano dalla scomparsa, l'interesse per l'attività di Majorana è stata intensa, anche per i suoi scritti inediti che non sono certo le carte più importanti per la scienza di oggi, ma che sono comunque del massimo interesse. Non sorprende allora che, nel luglio del 1946, la Gazzetta di Losanna abbia rivelato che il governo sovietico avesse tentato di venire in possesso delle carte di Majorana, oggi depositate alla Domus Galileana di Pisa. Le indagini su questo materiale privato, non destinato alla pubblicazione, pongono un problema di violazione della volontà dell'autore. Il caso si è gia presentato. Franz Kafka aveva lasciato all'amico Max Brod inidicazioni molto precise circa il destino delle sue opere: “ tutto ciò che mi lascio dietro (…) sotto forma di quaderni, manoscritti, bozzetti e così via, va bruciato fino all'ultima pagina senza essere letto”.
Come era successo a Virgilio, Kafka desiderava scomparire, ma Brod non gli obbedì affatto e le sue opere si salvarono e divennero nel tempo sempre più grandi. Furono pubblicate anche le lettere, ma ormai l'autore non poteva più protestare. In un momento di depressione, Flaubert aveva chiesto di essere sepolto con tutti suoi manoscritti inediti.
Come un guerriero con il suo cavallo. L'idea di pubblicare gli sembrava una sconvenienza, “come consentire a qualcuno di vederti nudo”. Ma le opere perdute emanano un fascino sottile ed un po' perverso. Per le carte, e più in generale per la personalità di Majorana, si parla di una sindrome che colpisce chiunque cominci ad occuparsene, confermata da un avvertimento di un esperto: “ per amor del cielo, ti imploro di desistere dall'occuparti di Majorana, i cui segreti e tormenti sono “cose che il tacer è bello” (per dirla con Dante), da temere ed evitare non meno delle passioni dei sensi, perché possono rubarti tutto il tuo tempo e privarti della salute, della serenità di spirito e della felicità”. Forse aveva ragione Amaldi sull'ossessione diffusa di indagare ai margini delle poche pubblicazioni che illustrano le ricerche di Majorana. Perché dovremmo voler leggere opere nascoste – forse volutamente nascoste, perché transitorie e marginali – quando ve ne sono moltissime che per forza di cosa potremmo leggere ed approfondire e non leggiamo?
L'avversione a non pubblicare, o comunque a non rendere noti i suoi risultati, faceva parte di un atteggiamento generale. Dopo il ritorno dal suo soggiorno di studio in Germania, Majorana era entrato in una fase di isolamento, trascorrendo sempre più le sue giornate in casa immerso nello studio. Più che di Fisica, in quel periodo si interessava di Economia politica. Al tempo stesso, gli interessi filosofici, che sempre erano stati vivi in lui, si erano fortemente accentuati, tanto da spingerlo a meditare a fondo le opere di vari filosofi, in particolare quelle di Schopenhauer. Che gli interessi di Majorana fossero molteplici, lo testimoniano un migliaio di suoi fogli manoscritti (formato protocollo) conservati presso la Domus di Pisa, di cui sinora solo un centinaio sono stati ordinati e titolati. Curiosamente, qualche foglio contiene i conteggi riguardanti le flotte da guerra delle grandi potenze (America, Francia, Germania, Giappone, Inghilterra, Italia) e dei loro rapporti di forza. Probabilmente, risale a quell'epoca il manoscritto sul valore delle leggi statistiche nella Fisica e nelle scienze sociali che, trovato fra le sue carte dal fratello Luciano, fu revisionato e pubblicato, con qualche refuso, a cura di Giovanni Gentile jr. con il titolo “Il valore delle scienze statistiche nella fisica e nelle scienze sociali” , sulla rivista “Scientia” nel 1942, quattro anni dopo la sua scomparsa.
Come riferisce Gentile nella presentazione del lavoro, “non fu pubblicato, forse per quella scontrosa reticenza che aveva l'Autore ad esprimersi con gli altri e che lo persuadeva troppo spesso a chiudere nel cassetto lavori anche importanti” . Il saggio – spiega ancora Gentile – ha una notevole importanza perché è proprio lì che Majorana assunse “una chiara posizione di fronte al dibattuto problema del valore statistico delle ultime leggi fisiche [si riferisce a quelle della Meccanica quantistica]. Questo che a molti sembra un difetto, come una denuncia di indeterminismo nel divenire della natura, è invece per il Majorana un motivo per rivendicare l'intrinseca importanza del metodo statistico, sinora nella sua essenza applicato solo nelle scienze sociali e che nella sua nuova interpretazione delle leggi fisiche ritrova intero il suo significato originario”.
Il lavoro si divide in tre parti: una prima, dedicata alla concezione della natura secondo la Fisica classica; una seconda, improntata ad una spiegazione del significato classico delle leggi statistiche e delle statistiche sociali; infine, vi è una discussione su come le nuove concezioni della Fisica influenzino anche una differente interpretazione delle realtà sociali.
Edoardo Amaldi, che tra i primi ha analizzato l'intera produzione scientifica di Majorana, spende non più di due parole per questo articolo. Indubbiamente, se confrontato con la profondità e il carattere pionieristico degli altri, questo è un lavoro “minore” ma a noi interessa più degli altri, poiché dimostra l'abilità di Majorana nella comunicazione scientifica verso il pubblico dei non specialisti.
Questa attività di (in)formazione scientifica annovera in quel tempo illustri esempi. Lo stesso Fermi scrisse su riviste dal titolo inequivocabile, Gerarchia o Gioventù Fascista , con articoli come Nuclei ed elettroni , Religione e Fascismo, Fede in Dio: La sapienza dei semplici. Può far sorridere pensare come la mente profonda e lucida di Fermi affrontasse i ridicoli argomenti pseudopolitici e pseudoreligiosi richiesti da simili riviste. Ma a tratti si riconosce il maestro: “peccato che fra le materie scolastiche non ve ne sia una che sarebbe la più importante: che insegni come studiare”. Ettore Majorana non fu coinvolto in queste iniziative editoriali, ma non sembra estraneo allo spirito del tempo, preparando (senza poi proporlo per la pubblicazione) questo articolo di natura divulgativa in cui si propone di presentare il punto di vista di un fisico sul valore delle leggi statistiche nelle scienze sociali alla luce delle nuove metafore quantistiche.
L'articolo risulta anch'esso pionieristico sia nella prospettiva fisica che in quella delle scienze sociali. In Fisica, ribadisce che le fluttuazioni quantistiche impongono l'uso di concetti statistici anche per eventi legati ad entità singole. Majorana osserva che le scoperte della Meccanica quantistica avrebbero avuto un notevole impatto. Avrebbero sicuramente permesso la descrizione dei sistemi (sub)atomici con il solo prezzo concettuale di introdurre una descrizione statistica anche per i processi elementari. Majorana si concentra, ad esempio, sull'osservazione che la Meccanica quantistica ha imposto di riconoscere che le leggi del decadimento radioattivo anche di un solo atomo devono tenere conto di un'intrinseca natura statistica. Per converso, pone enfasi sulla possibilità che queste leggi statistiche possano essere usate per i modelli dei sistemi finanziari e sociali. Majorana insiste nel far notare che la presenza degli inevitabili aspetti statistici dei fenomeni nucleari si impone come “ analogia essenziale ” per le scienze sociali, con una sostanziale identità di valore e di metodo.
Questo punto di vista insiste sulla necessità di usare le leggi statistiche in ogni disciplina scientifica. È un atteggiamento abbastanza inusuale per quel tempo, in cui si preferiva la descrizione deterministica dei sistemi economici sviluppata ad esempio da Pareto, Schlesinger e Wald nell'ambito della Meccanica classica. Le considerazioni proposte da Majorana si concentrano in modo innovativo sulla possibile analogia tra la natura quanto-statistica dei fenomeni nucleari e la formalizzazione dei modelli economici. Ritroviamo la critica all'eccessiva fiducia nel meccanicismo che, grazie alla precisione estrema con cui è in grado di prevedere la dinamica del sistema solare, aveva portato ad una generale tendenza ad estendere l'approccio deterministico della Meccanica celeste alle altre discipline, compresi “ i fenomeni più complicati dell'esperienza comune”.
Ritroviamo anche espressioni che avrebbe usato all'Università di Napoli, nel suo unico corso di Istituzioni di Fisica teorica. Parla così di sistema complesso statistico di stati microscopici, che potrebbe far intravedere da lontano addirittura la successiva formulazione della Meccanica quantistica di Feynman in termini di integrali di cammino.
Sulla critica al determinismo, che era un tema a lui molto caro, Majorana si lascia andare anche a qualche esternazione filosofica: “ la reazione filosofica, quando è stata felice, non è uscita dal suo campo, lasciando sostanzialmente intatto, se pur circoscritto nella sua importanza, il problema scientifico”. L'articolo non è sulle scienze sociali, ma sui metodi della Meccanica statistica. Lo chiarisce lo stesso Majorana con un ottimo uso della lingua: “ sarà nostro scopo ultimo l'illustrare il rinnovamento che il concetto tradizionale delle leggi statistiche deve subire in conseguenza del nuovo indirizzo seguito dalla fisica contemporanea ” ed aggiunge che “ è importante quindi che i principi della meccanica quantistica abbiano portato a riconoscere (oltre ad una certa assenza di oggettività dei fenomeni) il carattere statistico delle leggi ultime dei processi elementari. Questa conclusione ha reso sostanziale l'analogia tra fisica e scienze sociali, tra le quali è risultata un'identità di valore e di metodo .” Siamo ormai agli ultimi capoversi dell'articolo, Majorana intreccia profeticamente le nuove esigenze con la necessità di “ rivedere le basi dell'analogia (…) con le leggi statistiche sociali”, in conseguenza dei cambiamenti delle nuove teorie fisiche (Relatività e Meccanica quantistica) che prevede che indurranno una revisione anche nell'interpretazione delle leggi statistiche sociali.
Le idee “visionarie” di Majorana sulla natura intimamente stocastica dei fenomeni sociali inducono a proseguire nello sviluppo di un sottosettore, la Quanto-EconoFisica, in cui i concetti e le definizioni della Meccanica quantistica, le sue eventuali interpretazioni, applicazioni e generalizzazioni, possano permettere di descrivere più correttamente il comportamento dei processi economici. La naturale evoluzione di questo approccio è legato all'affermarsi della Teoria della relatività e della Meccanica quantistica che ha permesso di estendere il campo di indagine della Fisica sino ai confini delle interazioni fondamentali tra i suoi componenti più elementari. I numerosi successi della Teoria quantistica dei campi hanno profondamente modificato lo studio delle transizioni di fase od il comportamento dei sistemi caotici, studi che hanno raggiunto un notevole livello di maturità concettuale, con lo sviluppo di tecniche computazionali estremamente sofisticate. Teorie fisiche, come la teoria dei vetri di spin o la teoria del gruppo di rinormalizzazione, hanno permesso di avventurarsi nell'analisi di nuovi settori assimilabili a sistemi complessi. Gli studi di Statistica finanziaria cercano di far tesoro di tali risultati. Le diverse teorie di unificazione delle interazioni fondamentali, le teorie di gauge non abeliane, hanno fatto sentire i propri influssi una volta applicate nello studio dei tanti fenomeni legati agli esperimenti della big science , di quella Fisica (sub)nucleare su cui si è tanto investito ma che oggi appare in crisi perché troppo impegnativa per costi ed impegno umano. Questi risultati cominciano a rifluire negli studi economici e finanziari, tanto che si comincia a parlare di promettenti analogie tra le evoluzioni dei capitali finanziari ed interpretazioni legate a teorie di gauge quantizzate, come la Quanto-Elettro- Dinamica (QED) su reticolo. Ad esempio, la teoria del mercato dei capitali si traduce nello studio delle invarianze (di gauge ) dei flussi del campo monetario. Questo genere di modellizzazione dei mercati finanziari risulta promettente sia dal punto di vista formale che da quello applicativo.
L'Econofisica è una scienza seria?
“Le cose tutte quante/ hanno ordine fra loro (...)/
Ne l'ordine ch'io dico sono accline/
tutte nature, per diverse sorti,/
più al principio loro e men vicine;/
onde si muovono a diversi porti/
per lo gran mare de l'essere, e ciascuna/
con istinto a lei dato che la porti.”
Dante, La divina Commedia , Paradiso,
I 103-114
Malgrado tante potenzialità, alcuni economisti esprimono seri dubbi sull'utilità della modellizzazione dei sistemi economici con strategie e paradigmi propri della Fisica. Non si tratta solo del pregiudizio concettuale che i fisici non possono spiegare i complessi fenomeni legati alle scelte umane. Non si tratta neppure dell'avversione verso l'ingenuo determinismo di una teoria in grado di spiegare tutto, tipico dei primi approcci basati sulle leggi della Meccanica classica, con cui si presumeva di prevedere esattamente le evoluzioni finanziarie (come accade in Astronomia nel caso del moto dei pianeti). La critica maggiore è legata alla natura della limitata validità della formulazione fisica, legata a principi di invarianza e di conservazione difficilmente applicabile nei sistemi economici. Risulta difficile per un economista pensare di sbancare Wall Street partendo da una legge ipotetica di conservazione del denaro ed analizzando le conseguenze di una tale assunzione.
L'atteggiamento non è del tutto infondato, poiché è abbastanza evidente che una teoria di tipo economico non possa essere elaborata interamente su proposizioni di natura deduttiva, come è il caso delle teorie fisiche. La mancanza di un principio unificante da individuare, sviluppare e da sottoporre a verifica, implica necessariamente un maggior ricorso a costanti esogene e dunque, alla fin fine, la costruzione dei modelli risulterà meno logicamente concatenata di quanto non accada per ogni teoria fisica.
Del resto, se ci si spinge troppo lontano sulla strada della formulazione di teorie economiche su pochi principi generali, si rischia di ottenere previsioni sostanzialmente inutili. La questione non è risolta passando da semplicistiche analogie meccaniche alla proposizione di modelli termodinamici fondati sull'articolata parametrizzazione di equazioni alle derivate parziali. Si pensi alla nuova prospettiva aperta nel 1973 dai lavori di Black, Scholes e Merton (gli ultimi due insigniti del premio Nobel per l'Economia nel 1997, essendo Black già morto) nei quali si mostrava – non senza qualche errore – come un tipico problema finanziario potesse essere ricondotto all'equazione di diffusione del calore, ponendo le basi per lo sviluppo della finanza moderna, della teoria delle opzioni e dell'uso di equazioni differenziali stocastiche come algoritmo cardine nelle analisi del mercato dei titoli derivati e, più in generale, dello studio dei processi stocastici gaussiani. La formula di Black e Scholes, con le sue varianti, ha consentito numerose analisi empiriche diventando lo strumento operativo per eccellenza degli investitori professionali. Malgrado i successi, questi modelli (studiati spesso numericamente) non sempre forniscono buone previsioni. Dove il problema economico sia definito con sufficiente chiarezza, sono stati poi sviluppati modelli fisici in grado di fornire previsioni con un maggior grado di affidabilità e senza grandi operazioni di fine tuning . La strategia vincente è basata sul caratterizzare il problema con l'aiuto di economisti molto preparati in grado di elaborare un progetto di ricerca chiaro e definito. Il contributo fisico-matematico consiste poi nel saper far tesoro di tutta l'esperienza legata allo studio dei fenomeni fisici, per migliorare le possibilità di previsione del modello.
Se volessimo ricordare un esempio concreto della qualità d'approccio dell'Econofisica, potremmo riferirci al problema dello studio delle proprietà statistiche delle fluttuazioni temporali del mercato azionario ed in particolare della distribuzione della probabilità dei rendimenti. A partire dal 1950, analisi empiriche hanno mostrato bene come la distribuzione dei rendimenti azionari sia estremamente casuale e come le eventuali correlazioni tra rendimenti successivi svaniscano in brevi intervalli. Una tale situazione, detta a varianza trascurabile , permetterebbe (come già suggeriva Bachelier nel 1900) una trattazione probabilistica gaussiana. Purtroppo, questo approccio non risulta corretto in molte situazioni, sottostimando gli eventi estremi (nelle code), cioè le grandi perdite ed i grandi guadagni. In un mondo gaussiano, le crisi – come quella del 1929 – non potrebbero avvenire. Nel 1963, gli studi di Mandelbrot sui prezzi del cotone hanno suggerito che la non-gaussianità potesse essere associata ad una distribuzione di probabilità Levy stabile , cioè con correlazioni tali da avere momenti statistici superiori al secondo divergenti, in cui ovviamente gli eventi estremi sono sovrastimati.
Per anni, si è dibattuto sulle caratteristiche della distribuzione di probabilità dei rendimenti. Gli studi di Econofisica hanno potuto gettare nuova luce sul problema. I metodi ed i modelli economici standard sono in gran parte inadeguati a trattare il caso delle distribuzioni non-gaussiane osservate mentre l'approccio creativo, non convenzionale, proprio dell'Econofisica, risulta più promettente. Ciò si manifesta proprio nello studio di quelle situazioni in cui emergono le cosiddette leggi di scala , con la caratteristica dipendenza a potenza , tipica di una distribuzione iperbolica dell'evoluzione dei dati. Aiutati dall'avvento delle borse telematiche, che permettono il trattamento informatizzato di milioni di dati ad alta frequenza, i fisici hanno così cominciato a studiare le fenomenologia dei mercati, proponendo alcune congetture per arrivare ad una migliore comprensione delle dinamiche complesse che governano il mercato –inteso come complesso sistema di elementi interagenti – slegandosi dalla mera ricerca della distribuzione di probabilità più adatta a descrivere la natura stocastica e concentrandosi sui meccanismi, le correlazioni dinamiche, che generano queste distribuzioni che hanno code diverse e “più grasse” delle gaussiane. Corollario matematico essenziale di questi studi è rappresentato dalla conoscenza delle regole dei processi stocastici che trovano da sempre grande impiego nello studio delle fluttuazioni dei prezzi nei mercati finanziari.
La Meccanica statistica e lo studio dei cammini aleatori a tempo continuo contribuiscono ulteriormente alla definizione della dinamica dei mercati finanziari. Problemi come:
• leggi di potenza e di scaling
• interazioni e proprietà di insiemi di beni
• non ergodicità dei mercati finanziari
forniscono oggi il principale oggetto di indagine per verificare la validità degli approcci formali delle scienze fisiche. Nel tempo, tuttavia, i fisici si sono occupati di altre applicazioni non legate necessariamente al campo finanziario, occupandosi anche della distribuzione, della dimensione e della crescita delle aziende, delle città e della qualità delle scoperte scientifiche. La Meccanica statistica resta la principale ispirazione concettuale per gran parte di questi problemi ma, come asseriva Majorana, resta la convinzione di un'identità essenziale tra questi metodi usati in Fisica e le scienze sociali.
Attualmente, non si conosce un modello matematico deterministico che descriva il comportamento della dinamica dei prezzi nei mercati finanziari. Da un punto di vista microscopico, i mercati sono costituiti da un insieme di persone che effettuano transizioni agendo in modo individuale e relativamente semplice. La complessità di questo sistema risiede nel fatto che, dall’interazione di questi soggetti, emergono effetti collettivi (l’andamento dei prezzi delle azioni, per esempio) non immediatamente riconducibili alle scelte operate dai singoli. Trovare le sofisticate regole per prevedere la variazione del prezzo delle azioni è considerato uno dei più complessi problemi di tutta la Statistica finanziaria.
La maggior parte dei modelli matematici concretamente usati dagli analisti finanziari è riconducibile ai risultati ottenuti nel 1973 da Fischer Black e Myron Scholes con qualche utile contributo di Robert Merton, migliorando un precedente approccio sviluppato da A. James Boness, nella sua tesi di
dottorato all’Università di Chicago. Black era un fisico, Scholes un matematico, Merton aveva iniziato la sua carriera universitaria come ingegnere elettronico. Il loro modello, nella sua forma più semplice, mostra che l’evoluzione del prezzo dei titoli derivati verifica un’equazione differenziale alle derivate parziali parabolica, riconducibile all’equazione
di diffusione del calore.
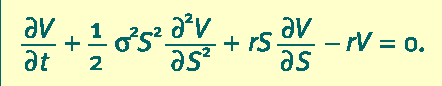
Fig. 1 L’equazione di Black e Scholes per l’evoluzione del valore V(S, t) di una particolare opzione, di un titolo o di uno strumento derivato basato sul prezzo di mercato S di un bene (azione, valuta, …) all’istante t, dove r rappresenta il tasso d’interesse senza rischi e σ la volatilità.
Sono possibili diverse derivazioni dell’equazione. Nel loro lavoro originale del 1973, Black e Scholes si limitano a considerare particolari opzioni senza rischi. Le successive generalizzazioni del modello si avvalgono dei metodi avanzati del calcolo probabilistico, di solito impiegati nella descrizione dei processi stocastici.
L’uso di questi processi nel campo dei modelli finanziari può essere fatto risalire ad una tesi di dottorato in Matematica dal titolo La teoria della speculazione, discussa il 29 marzo 1900 da Louis Bachelier, in cui si avanzava l’ipotesi di applicare la teoria della probabilità allo studio della variazione dei prezzi dei titoli di stato emessi dal governo francese.
L’approccio introdotto dalla tesi, giudicata onorevole (poco più che mediocre) dalla commissione esaminatrice, che vantava la presenza di Henri Poincarè, esportava in ambito finanziario i metodi probabilistici per studiare i processi di diffusione e più in generale introduceva il concetto di processo stocastico con variazione continua.
Sebbene non avesse avuto inizialmente grande risonanza, l’approccio anticipava di cinque anni tutte le caratteristiche essenziali della teoria sviluppata da Einstein per descrivere i cammini caotici del moto dei granelli di polline in sospensione in un liquido, osservati sin dal 1827 dal botanico inglese Robert Brown. Nel 1905, il suo annus mirabilis, Einstein analizzò
il fenomeno browniano sia a livello microscopico sia macroscopico. A livello microscopico descrisse il moto dei granelli di polline, i cui cambiamenti repentini di direzione sono dovuti agli urti con le molecole d’acqua. Non potendo conoscere con precisione le condizioni iniziali, l’unico modo per modellizzare questo sistema fu di passare ad un livello macroscopico, proponendo una formulazione statistica per il moto del polline. L’effetto cumulativo degli urti porta la particella a muoversi in modo casuale, come se si trovasse su un reticolo e potesse muoversi con determinate probabilità.
Questo tentativo serviva ad Einstein per ribadire la natura molecolare ed atomica della materia. Le diffidenze nella comunità scientifica furono superate solo qualche anno dopo, con i risultati di una serie di esperimenti condotti da Perrin.
Malgrado questi successi, la teoria di Einstein dei processi legati al moto browniano non aveva una solida base matematica, introdotta solo (dal 1918 al 1923) in alcuni brillanti lavori del matematico Norbert Wiener. Il modello matematico del moto caotico fondato su processi elementari, oggi detti di Wiener, ha ispirato la formulazione di un modello macroscopico del mercato finanziario secondo il quale i prezzi delle azioni, risultanti da una serie di trattazioni di cui ignoriamo la dinamica microscopica, sono aleatori e la loro distribuzione di probabilità è la curva di Gauss.
Nel corso degli anni si evidenziarono i limiti di quest’approccio gaussiano (à la Bachelier), che non riproduceva in modo soddisfacente l’andamento dei prezzi. In particolare, Paul Samuelson, del MIT di Boston, analizzò con attenzione nel 1955 le analogie tra le proprietà del moto caotico browniano e la dinamica dei mercati finanziari. Nel 1962, James Boness, si focalizzò sullo studio dei titoli derivati anticipando, di fatto, i risultati del modello formulato nel 1973 da Black, Scholes e Merton, che è oggi considerato il modello standard della dinamica dei prezzi nei mercati finanziari.
In questo modello, la soluzione dell'equazione può essere ottenuta tramite il metodo della separazione delle variabili (utilizzato da Black e Scholes nel loro lavoro) oppure sfruttando alcune strategie di calcolo derivate dalla Fisica teorica, come la formula di Feynman-Kac che fornisce una rappresentazione della soluzione, utilizzando le proprietà probabilistiche dei processi stocastici e aprendo così la via a soluzioni numeriche tramite simulazioni con metodi Monte Carlo. Emerge che il logaritmo del prezzo di un'azione si comporta come la posizione di una particella in un moto browniano: ne segue che i prezzi hanno una distribuzione di probabilità lognormale. Successive generalizzazioni hanno portato allo sviluppo di una teoria completa della dinamica dei prezzi speculativi. Non estraneo a questi sviluppi è risultato il gran lavoro fisico-matematico legato allo studio delle analogie tra l'equazione di diffusione del calore e l'equazione differenziale alle derivate parziali di Black e Scholes. È un nesso non casuale tra Fisica e Finanza che ha permesso di esportare molte delle numerose competenze legate alla descrizione teorica del fenomeno fisico in ambito finanziario.
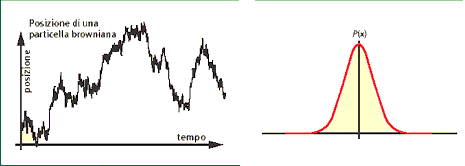
Fig. 2 La posizione di una particella in un moto caotico browniano unidimensionale, confrontato, sotto, con il tipico andamento del prezzo di un'azione. A destra, la tipica distribuzione di probabilità di Gauss.
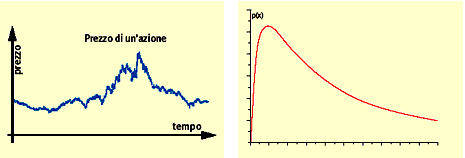
Fig. 3 A destra, una distribuzione di probabilità lognormale non ha una forma “a campana” simmetrica rispetto al suo massimo.
Bibliografia
- Decio Cocolicchio, Luca Grilli, Lucia Maddalena, Econofisica: Metodi per l'economia , Raccolta di applicazioni , Edizioni Scientifiche Italiane, 2006.
- Joseph L. McCauley, Dynamics of Markets: Econophysics and Finance, Cambridge Univ. Press, 2004.
- Rosario N. Mantegna, H. Eugene Stanley, An Introduction to Econophysics, Cambridge Univ. Press, 1999.
