Henri Poincaré a 100 anni dalla morte (1854-1912)
Henri Poincaré a 100 anni dalla morte (1854-1912)
- La stella più brillante nel cielo di Hermite
- Il "cervello vivente delle scienze razionali" si è spento
1. La stella più brillante nel cielo di Hermite
Charles Hermite (1822-1901) scrivendo a Mittag-Leffler (1846-1927) il 4 marzo 1882 a proposito della sistemazione di una scintillante schiera di giovani matematici, parlava di tre stelle nel cielo della matematica francese. Le tre stelle erano Paul Appell, suo parente acquisito (avendo sposato una nipote), Émile Picard, suo genero, e Henri Poincaré che aveva appena avviato le sue ricerche sulle funzioni fuchsiane. Ma subito dopo Hermite precisava il suo orientamento: «Posso sussurrare nel suo orecchio, molto temendo che la signora Hermite possa sentirmi, che a me Poincaré sembra la [stella] più brillante». Il giudizio di Hermite segnava l'avvio di una strepitosa e inarrestabile avventura scientifica.
Paul Appel, Émile Picard e Henri Poincaré
Henri Poincaré era nato a Nancy il 29 aprile 1854. I suoi genitori erano entrambi della Lorena (Neufchâteau, nei Vosgi). Era stato educato in un ambiente colto e laborioso, dove l'esempio sollecitava l'attività personale. Il nonno paterno, Jules Nicolas, era farmacista a Nancy, dove nacquero i suoi tre figli, fra cui, nel 1828, Léon – il padre di Henri – e nel 1829, Antoni – padre di Raymond Poincaré, Presidente della Repubblica durante la prima guerra mondiale. Léon Poincaré era medico e docente alla Facoltà di medicina di Nancy. Il fratello Antoni divenne invece ispettore generale dei ponti e strade, ed è noto per aver rifiutato il giuramento dopo il colpo di stato del 1852.
La madre di Poincaré, Eugénie Launois (1830-1897), originaria da una famiglia di Arrancy (Mosa), dedicava tutte le sue cure all'educazione dei suoi due figli, Henri e la sorella Aline, di poco più giovane. Anche Aline era una donna molto intelligente ed è stata una preziosa collaboratrice del marito, il filosofo Émile Boutroux.
È in questo ambiente, di una élite di studiosi e di accademici, che si svolse l'infanzia di Henri Poincaré. Un'infanzia particolarmente felice, grazie alle qualità naturali di cui egli era dotato, ma anche grazie alle cure di cui era circondato.
Tutti i suoi biografi concordano nel considerare Poincaré uno studente tutt'altro che modello, e già votato da ragazzo allo studio della matematica.
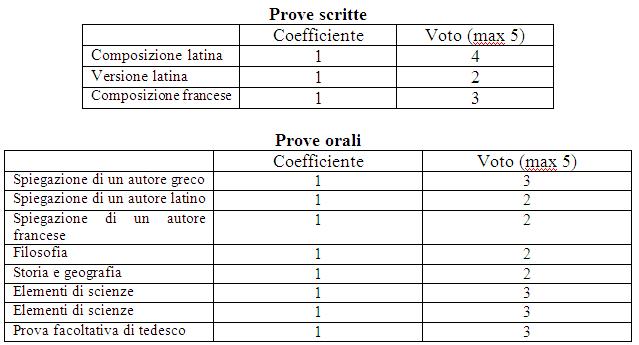
Al Liceo di Nancy, quando si trattò di scegliere fra proseguire gli studi per ottenere il diploma in lettere o in scienze, scelse le lettere. Ottenne il baccalaureato (maturità) il 5 agosto 1871 con il giudizio globale di “buono” e con i seguenti punteggi analitici – tutt'altro che brillanti – [Appell 1925, p. 18]:
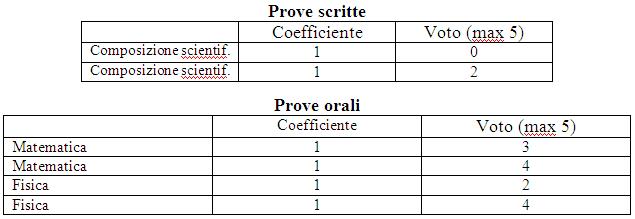
Successivamente, durante le vacanze estive, Poincaré si preparò per il diploma speciale per gli studi scientifici, sostenuto poi il 7 novembre 1871. Ancora un risultato non particolarmente brillante stando al quadro dei risultati [Appell 1925, p. 19)]:
Dunque Poincaré subì uno scacco, e proprio nella prova scritta di matematica, per la quale rischiò di essere bocciato. Sembra che fosse arrivato tardi e avesse frainteso l'argomento. Inutile dire che si è salvato brillantemente all'esame orale, al quale però non avrebbe potuto essere ammesso.
In possesso dei due diplomi, Poincaré cominciò gli studi preparatori per l'ammissione ad una delle due grandi scuole superiori, l'École Polytechnique e l'École Normale. Seguì cioè, e con successo, i corsi di matematiche elementari (1871-72) e di matematiche speciali (1872-73) presso l'École forestière, dove incontrò Paul Appell (1855-1930). Quest'ultimo scelse l'École Normale, mentre Poincaré – forse seguendo l'esempio ed i consigli della famiglia – scelse l'École Polytechnique, i cui corsi seguì nel biennio 1873-75. Alla fine del biennio, entrò nell'École des Mines, dove terminò i suoi studi nel 1878.
Da quello che si sa, Poincaré ha svolto coscienziosamente i suoi doveri professionali: nel breve periodo in cui ha lavorato come ingegnere minerario nel sub-distretto mineralogico di Vesoul (Alta Saona), si fece notare per il temperamento e l'attaccamento al dovere. Nonostante il pericolo che lo minacciava, non esitò a scendere in un pozzo di miniera dove una esplosione di grisou aveva fatto sedici vittime e provocato un incendio.
Mentre si preparava ad essere un buon ingegnere, Poincaré inizia a dedicarsi alla ricerca scientifica: comincia non da temi specifici, ma da questioni importanti e difficili [Poincaré 1878]. Nel 1879 ottiene il dottorato in matematica, presentando un lavoro sull'integrazione di equazioni differenziali alle derivate parziali in un qualsiasi numero di variabili indipendenti [Poincaré 1879]. La commissione era composta da Ossian Bonnet (1819-1892), da Claude Bouquet (1819-1885) e da Gaston Darboux (1842-1917, relatore). Entrambi i lavori prima citati “rivelano una mente profonda e originale, e sono stati il presagio del futuro scienziato brillante” [Darboux 1913, p. 16]. Non meraviglia perciò che, pochi mesi dopo la discussione della tesi, il 1° dicembre 1879, Poincaré sia incaricato dei corsi di Analisi presso la Facoltà di Scienze di Caen.
Darboux approfitta di questo momentaneo distacco di Poincaré da Parigi per sottolineare anch'egli – facendo eco al già citato giudizio di Hermite – le speranze riposte sulla nuova generazione di matematici: «Quando mi riporto a quel 1879, penso alle speranze che ci dava per lo sviluppo degli alti studi matematici nel nostro paese. Due geometri, un po' più giovani di Poincaré, costituivano come lui, e forse contro la loro volontà, l'ornamento delle nostre Facoltà di provincia. Mentre Poincaré era a Caen, Paul Appell insegnava Meccanica razionale a Dijion, Emile Picard insegnava Analisi matematica a Toulouse. […] Due anni dopo, i tre giovani rientravano, per rimanere permanentemente annessi alla Facoltà di Parigi».
Poincaré, in particolare, nell'anno 1881-82 verrà nominato docente di Analisi alla Sorbona. Quattro anni più tardi, sarà responsabile dei corsi di meccanica e fisica sperimentale e, infine, nell'agosto del 1886, prenderà il posto di Lippmann sulla cattedra di Fisica matematica e probabilità.
I suoi lavori fatti durante questo periodo giovanile giustificavano una progressione di carriera così rapida. Trattavano la teoria delle equazioni differenziali e alle derivate parziali, la teoria generale delle funzioni analitiche di una o più variabili, la meccanica analitica e la meccanica celeste, l'algebra e la teoria dei numeri.
Questo complesso di lavori conteneva “risultati interamente nuovi, scoperte analitiche che hanno fatto dire ad uno dei nostri maestri [Hermite] che Poincaré esordiva come Cauchy”. Tra questi lavori, si segnala in primis [Poincaré 1881], un lavoro del tutto originale sulle equazioni differenziali, presentato all'Accademia nel 1880, e soprattutto il complesso dei lavori sulla teoria delle funzioni fuchsiane occorre segnalare. L'occasione per l'avvio della sua opera più brillante era stata data dal concorso bandito dall'Académie des Sciences per il gran premio delle Scienze Matematiche del 1880, sul tema: «Perfezionare in un punto importante la teoria delle equazioni differenziali lineari ad una sola variabile».
Il premio fu assegnato a George Halphen (1844-1889), ma Poincaré aveva presentato al concorso – il 22 marzo 1880 – un lavoro che adottava il motto orgoglioso della sua città natale: Non inultus premor (“Nessuno mi tocchi impunemente”), e che fu ben giudicato dalla giuria come si evince dal resoconto di [Hermite 1881]:
| […] l'autore affronta successivamente due questioni completamente diverse, di cui fa uno studio completo con un talento che ha estremamente colpito la Commissione. La seconda questione, che riceve gli sviluppi più ampi, riguarda le belle e importanti ricerche di Fuchs, di cui indicheremo brevemente l'argomento. Il signor Fuchs si è proposto di determinare quali condizioni permettono di definire una funzione quando si eguaglia ad una indeterminata il quoziente degli integrali di una equazione differenziale lineare del secondo ordine. I risultati così notevoli del geometra tedesco presentavano alcune lacune che l'autore ha riconosciuto e segnalato, completando così una teoria analitica estremamente interessante. Questa teoria gli ha suggerito l'origine di trascendenti che comprendono, in particolare, le funzioni ellittiche, e che permettono di ottenere, in casi molto generali, la soluzione di equazioni lineari del secondo ordine. Si ha così una via fruttuosa che l'autore non ha percorso nella sua interezza, ma che testimonia uno spirito inventivo e profondo. La Commissione non può che invitarlo a continuare la ricerca, segnalando all'Accademia il bel talento messo in mostra. |
È interessante leggere le circostanze nelle quali Poincaré pervenne a superare le difficoltà legate a questa ricerca. Lo racconta egli stesso in [Poincaré 1908a], una delle più note delle sue opere epistemologiche, ed il racconto è stato poi divulgato anche dai redattori dell'Enseignement mathématique, a proposito dell'inchiesta sulle abitudini mentali dei matematici. Dice Poincaré:
| Da quindici giorni mi stavo sforzando di dimostrare che non poteva esistere alcuna funzione analoga a quelle che ho chiamato da allora funzioni di Fuchs (…). Tutti i giorni mi sedevo al mio tavolo da lavoro, ci passavo un'ora o due, provavo un gran numero di combinazioni e non pervenivo ad alcun risultato. Una sera, contrariamente alle mie abitudini, bevvi del caffè nero; non riuscivo ad addormentarmi, le idee mi si affollavano; le sentivo come urtarsi, fino a che due di loro si addensarono, per così dire, a formare una combinazione stabile. Al mattino, avevo stabilito l'esistenza di una classe di funzioni fuchsiane, quelle che derivano dalla serie ipergeometrica. Avevo solo da scrivere i risultati, ciò che mi prese solo poche ore.
Volli in seguito rappresentare queste funzioni come quoziente di due serie; l'idea era perfettamente cosciente e deliberata; mi guidava l'analogia con le funzioni ellittiche. Mi chiedevo quali dovessero essere, se esistevano, le proprietà di queste serie, e arrivai senza difficoltà a formare le serie che ho chiamato tetafuchsiane. Ero sul punto di lasciare Caen, dove vivevo allora, per partecipare ad una spedizione geologica organizzata dall'École des Mines. Gli eventi del viaggio mi fecero dimenticare i lavori matematici; arrivati a Coutances [bassa Normandia], siamo entrati in un omnibus per non so quale passeggiata. Nel momento in cui mettevo piede sul predellino, mi venne in mente, senza che nulla nei miei pensieri precedenti sembrava avermi preparato, che le trasformazioni che avevo usato per definire le funzioni fuchsiane erano identiche a quelle della geometria non euclidea. Non ho controllato, non ne avrei avuto il tempo perché, appena sull'autobus, ho ripreso la conversazione iniziata, ma ho sentito una perfetta certezza. Di ritorno a Caen, ho verificato il risultato a mente serena per scrupolo di coscienza. Ho iniziato allora a studiare questioni di aritmetica senza molto risultato apparente, e senza sospettare che questo potesse avere qualcosa a che fare con i miei studi precedenti. Disgustato del mio fallimento, sono andato un paio di giorni al mare e ho pensato a qualcos'altro. Un giorno, mentre camminavo sulla scogliera, mi venne in mente, sempre con le stesse caratteristiche di brevità, subitaneità e immediata certezza, che le trasformazioni aritmetiche delle forme quadratiche ternarie indefinite erano identiche a quelle della geometria non euclidea. Tornato a Caen, ho riflettuto su questo risultato e ne ho tratto le conseguenze; l'esempio delle forme quadratiche mi mostrava che ci sono gruppi fuchsiani diversi da quelli corrispondenti alla serie ipergeometrica, vidi che avrei potuto applicare loro la teoria delle funzioni thêtafuchsiane, e che quindi esistevano funzioni tetafuchsiane diverse da quelle derivate dalla serie ipergeometrica, le uniche che conoscessi allora. Naturalmente mi proposi di formare tutte queste funzioni. (…) Ma tutti i miei sforzi servirono solo ad aumentare la consapevolezza dei miei problemi, che era già qualcosa. Tutto questo lavoro fu perfettamente cosciente. A questo punto, partii per Mont-Valérien, dove dovevo fare il servizio militare. Così ho avuto problemi molto diversi. Un giorno, attraversando il corso, mi apparve di colpo la soluzione delle difficoltà che mi avevano bloccato. Non ho cercato di approfondirla subito, e fu solo alla fine del mio servizio che ho ripreso la questione. Avevo tutti gli elementi, bastava raccoglierli e ordinarli. Così ho scritto tutto di getto, e senza problemi, la mia Memoria. |
Non si può ignorare, di questo intenso periodo iniziale di attività scientifica, il bel gruppo di lavori dedicati alla teoria dei numeri, efficacemente analizzati dallo stesso Poincaré, che già nel 1881 gli valsero la prima segnalazione nell'elenco dei candidati alla Académie per la sezione di Geometria. E ancora le sue ricerche sulle funzioni omogenee e la regola dei segni di Cartesio; la dimostrazione, svolta in collaborazione con Picard, del famoso teorema di Riemann sulle funzioni uniformi di n variabili a 2n periodi [Poincaré 1883a]; l'attacco al problema dell'uniformizzazione delle funzioni analitiche [Poincaré 1883b], che ha preparato la definitiva soluzione di esso circa un quarto di secolo dopo; i suoi studi sui determinanti di ordine infinito, sulle funzioni teta di più variabili, sulle funzioni iperfuchsiane introdotte da Émile Picard (1856-1941), sulla riduzione degli integrali abeliani, sugli integrali impropri delle equazioni lineari, ecc.
Poincaré non ignorava l'alto valore dei suoi scritti; mentre altri avrebbero chiesto premi, lui al contrario non chiedeva nulla. “Lo consideravamo tutti come il più forte fra noi. (…) Nessuno poteva prevedere i molti vuoti che la morte avrebbe prodotto nella sezione di geometria. Per farlo arrivare più rapidamente, per garantirgli un posto nella sezione di Astronomia, gli si segnalavano le applicazioni che le teorie da lui scoperte avrebbero potuto trovare in Meccanica celeste. Egli seguiva docilmente queste indicazioni, affrontava il problema dei tre corpi, le figure dei corpi celesti, e trovava del tutto naturale lasciar passare davanti a lui tutti quelli più anziani” [Darboux 1913, p. 23].
Come si è già detto, fin dal 1881, alla morte di Chasles, la Sezione di Geometria l'aveva fatto figurare nelle sue liste di presentazione. Vi era stato mantenuto dopo la morte di Puiseux, di Serret, di Bouguet. La morte prematura di Laguerre gli procurò il posto, ed egli fu eletto, il 24 gennaio 1887, con 31 voti su 55 votanti. Così entrò all'Académie all'età di 32 anni.
Questo primo successo fu seguito da un altro altrettanto sorprendente.

Oscar II di Svezia
Nel 1885, il re di Svezia, Oscar II, su proposta di Mittag-Leffler, (1846-1927) inaugurava una serie dei riconoscimenti internazionali, decidendo di assegnare il 21 gennaio 1889, sessantesimo suo compleanno, un premio per una scoperta importante nel campo della Analisi matematica. Il premio consisteva in una medaglia d'oro con l'effigie del re e una somma di 2500 corone svedesi. Una Commissione – composta da Karl Weierstrass (1815-1897), da Charles Hermite e dal fondatore (e caporedattore) degli Acta Mathematica, Mittag-Leffler, professore nell'Università di Stoccolma – venne incaricata di realizzare le intenzioni di Sua Maestà e sviluppare il programma del premio proposto. Essa indicò quattro argomenti diversi fra i quali i concorrenti potevano scegliere. Riportiamo qui di seguito i titoli dei quattro temi proposti, quasi tutti di natura tale da interessare Poincaré:
| I. Dato un sistema qualunque di punti materiali che si attraggono mutuamente secondo la legge di Newton, si propone, nell'ipotesi che non abbiano mai luogo urti fra due punti, di rappresentare le coordinate di ogni punto sotto forma di serie che procedano secondo funzioni note del tempo e che convergano uniformemente per ogni valore reale della variabile.
Questo problema, la cui soluzione amplierà significativamente la nostra conoscenza in relazione al sistema del mondo, sembra potersi risolvere con mezzi analitici a nostra disposizione; presumibilmente almeno, perché Lejeune-Dirichlet ha comunicato, poco prima della sua morte, ad uno dei suoi amici matematici [Leopold Kronecker], di aver scoperto un metodo per l'integrazione delle equazioni differenziali della Meccanica, applicando il quale era riuscito a dimostrare in maniera rigorosa la stabilità del nostro sistema planetario. Purtroppo, non sappiamo nulla di questo metodo, tranne che la teoria delle oscillazioni infinitamente piccole sembra essere stata il punto di partenza della sua scoperta. Si può però presumere, quasi con certezza, che questo metodo non si basava su calcoli lunghi e complicati, ma sullo sviluppo di un'idea semplice e fondamentale, che si può, con ragione, sperare di ritrovare con un lavoro perseverante e approfondito. Nel caso poi in cui il problema proposto non riuscisse ad essere risolto al momento del concorso, si potrebbe assegnare il premio ad un lavoro in cui fosse stato trattato nel modo indicato e risolto completamente qualche altro problema di Meccanica. II. Fuchs ha dimostrato in parecchie sue Memorie che esistono funzioni uniformi di due variabili, che si collegano per la loro formazione alle funzioni ultraellittiche, ma più generali, e che potrebbero forse acquistare una grande importanza per l'Analisi se la loro teoria fosse maggiormente sviluppata. Si propone di ottenere in forma esplicita, in un caso abbastanza generale, le funzioni la cui esistenza è stata provata da Fuchs, in modo che si possano riconoscere e studiare le loro proprietà più essenziali. III. Lo studio delle funzioni definite da una equazione differenziale sufficientemente generale del primo ordine, il cui primo membro sia un polinomio intero e razionale rispetto alla variabile, alla funzione e alla sua derivata prima. Briot e Bouquet hanno aperto la via ad un tale studio nella loro Memoria sull'argomento. I matematici che conoscono i risultati scoperti dai due autori per primi, sanno anche che il loro lavoro è lungi dall'aver esaurito l'argomento, difficile ed importante. Sembra probabile che nuove ricerche, intraprese nella stessa direzione, possano condurre a proposizioni di elevato interesse per l'Analisi. IV. È nota quale luce sia stata gettata sulla teoria generale delle equazioni algebriche dallo studio delle equazioni speciali cui conduce la divisione del cerchio in parti eguali, e la divisione per un numero intero dell'argomento delle funzioni ellittiche. La trascendente così notevole che si ottiene esprimendo il modulo della teoria delle funzioni ellittiche mediante il quoziente dei periodi, conduce analogamente alle equazioni modulari che hanno dato origine a nozioni interamente nuove ed a risultati di grande importanza, come la risoluzione delle equazioni di quinto grado. Ma questa trascendente è solo il primo termine, il caso particolare più semplice di una serie infinita di nuove funzioni che Poincaré ha introdotto nella scienza con la denominazione di “funzioni fuchsiane”, e che ha applicate con successo all'integrazione delle equazioni differenziali lineari di ordine qualunque. Queste funzioni dunque, che hanno in Analisi un ruolo evidente, non sono state considerate finora dal punto di vista algebrico, come la trascendente della teoria delle funzioni ellittiche di cui sono figlie. Si propone di colmare tale lacuna e di pervenire a nuove equazioni analoghe alle equazioni modulari, studiando, anche in un caso particolare, la formazione e le proprietà delle relazioni algebriche che legano due funzioni fuchsiane quando hanno un gruppo comune. |
Poincaré scelse il primo, certamente il più difficile ma anche il più attraente, che trattò – avvalendosi della larghezza che veniva offerta dalla commissione – con l'introduzione di uno studio generale delle equazioni della dinamica e limitando ad alcuni casi particolari la discussione del problema dei tre corpi. La Memoria di Poincaré, che portava il motto: Nunquam praescriptos transibunt sidera fines [Mai i corpi celesti supereranno i limiti loro prescritti], era stata molto apprezzata dai tre giudici, come gli scrive Mittag-Leffler, in forma strettamente confidenziale, il 15 novembre 1888, ma tuttavia aveva bisogno di qualche aggiunta, soprattutto riguardo alle omesse dimostrazioni di molti teoremi:
| Hermite, Weierstrass ed io abbiamo terminato lo studio della sua Memoria. Mi permetto di confidarle, pregandola del silenzio più assoluto, che siamo dell'opinione unanime che lei ha fatto di nuovo un capolavoro di primo rango e che la pubblicazione della sua Memoria sarà l'inizio di un'epoca nuova in Meccanica celeste. Ma non voglio affatto nasconderle che lo studio del suo lavoro ci è parso presentare grandi difficoltà. Lei omette molto spesso le dimostrazioni dei teoremi molto generali e molto difficili oppure dà indicazioni talmente brevi che bisogna tormentarsi per giorni prima di riuscire a valutare correttamente la profondità delle sue idee. Weierstrass mi ha chiesto se, profittando dell'amicizia di cui lei mi onora da tempo, osavo chiederle la disponibilità ad aggiungere alla Memoria, prima della pubblicazione, alcuni sviluppi sui punti essenziali che sono stati trattati fin qui in maniera troppo breve. |
Analogo il pensiero di Hermite, espresso in due lettere a Mittag-Leffler, che aggiunge un prezioso dettaglio biografico su Poincaré:
| La Memoria di Poincaré è di una profondità e di una potenza inventiva molto rare, e farà certamente epoca nella scienza sia dal punto di vista dell'analisi sia per le conseguenze astronomiche. Ma sarebbero necessari degli sviluppi molto più estesi e per ora sto chiedendo all'eminente autore di darmi schiarimenti su parecchi punti importanti. […]
Io le confesso in maniera del tutto formale che leggendo la Memoria di Poincaré mi sono dedicato poco ad approfondire le dimostrazioni dei suoi teoremi e a verificarne l'esattezza e di più a rendermi conto della loro importanza. È sotto l'impressione di un profondo sentimento di ammirazione per l'invenzione che in questa Memoria brilla di uno splendore così vivo che io le scrivevo giorni fa e non dubito che lei e Weierstrass condividete questa opinione. Ma bisogna pur riconoscerlo, in questo lavoro, come in quasi tutte le sue ricerche, Poincaré mostra bene la via e dà le indicazioni, ma lascia un considerevole lavoro da fare per colmare le lacune e completare l'opera. |
Alla scadenza del premio, fissata all'1 giugno 1888, le Memorie pervenute risultavano dodici, così suddivise fra i quattro temi: cinque riguardavano il tema n. 1, una era relativa al tema n. 3, mentre le sei rimanenti erano relative a tematiche alternative. Sarà Edvard Phragmén (1863-1937), un collaboratore di Mittag-Leffler, ad occuparsi di una prima selezione delle Memorie e a inviarne copia ai commissari. Alla fine di questa procedura, restarono in competizione solo tre Memorie, fra cui quelle di Poincaré e del suo amico Appell. La commissione, malgrado la difficile comprensione del testo, assegna la vittoria a Poincaré e attribuisce ad Appell una menzione onorevole.
Come previsto dal bando, a Poincaré spettava, in aggiunta alla medaglia d'oro, un sostanzioso premio in denaro e la pubblicazione su Acta Mathematica, cosa che avverrà malgrado alcuni rilievi di “oscurità del testo” – sollevati da Phragmén nel corso della messa a punto del manoscritto – e malgrado un errore più sostanziale scoperto invece dallo stesso Poincaré.
È comunque a partire dal successo riportato nel premio svedese che il nome di Poincaré viene conosciuto anche dal grande pubblico e il matematico considerato non più come una grande speranza, ma come uno studioso di cui la Francia “aveva il diritto di andare orgogliosa”. Né il successo attenua la sua straordinaria capacità di lavoro, documentata dai corsi che Poincaré tiene su temi costantemente rinnovati. Lo attestano i volumi in cui quei corsi sono pubblicati, a cura delle associazioni studentesche che ne raccoglievano le lezioni. Si tratta di una quindicina di testi i cui titoli testimoniano anche la vastità degli argomenti trattati, quasi tutti nuovi per lui:
| Potentiel et Mécanique des Fluides, corso dell'anno 1885-86 (a cura di Guillet).
Théorie Mathématique de la Lumière, I, corso del primo semestre 1887-88 (a cura di Jules Blondin). Thermodynamique, corso del primo semestre 1888-89 (a cura di Blondin). Électricité et Optique, Tome I: Les théories de Maxwell et la théorie électromagné-tique de la lumière, corso del secondo semestre 1888-1889 (a cura di Blondin). Tome II: Les théories de Helmholtz et les expériences de Hertz, corso del secondo semestre 1889-90 (a cura di Brunhes). Capillarité, corso del secondo semestre 1888-89 (a cura di Blondin). Leçons sur la théorie de l'élasticité, corso del primo semestre 1890-91 (a cura di Borel e Drach). Théorie Mathématique de la Lumière, II: Nouvelles études sur la diffraction. Théorie de Helmholtz, corso del primo semestre 1891-92 (a cura di Lamotte e Hurmuzescu). Théorie des Tourbillons, corso del secondo semestre 1891-92 (a cura di Lamotte). Les Oscillations électriques, corso del primo semestre 1892-93 (a cura di Maurain). Théorie analytique de la propagation de la chaleur, corso del primo semestre 1893-1894 (a cura di Royer e Baire). Calcul des Probabilités, corso del secondo semestre 1893-94 (a cura di Quiquet). Théorie du Potentiel newtonien, corso del primo semestre 1894-95 (a cura di Le Roy e Vincent). Électricité et Optique. La lumière et les théories électrodynamiques, corso del 1899 (a cura di Blondin e Néculcéa). |
I corsi della Sorbona si vanno ad aggiungere, per altro, a quelli tenuti presso l'École Polytechnique (1904-1908) e presso la “Scuola professionale delle Poste e Telegrafi” (dal 1904 al 1910). Ovunque, Poincaré passa in rassegna i princìpi generali ed i concetti base delle scienze sperimentali: principio di conservazione dell'energia, principio di Carnot, i concetti di entropia, di etere, di radiazione, di azione, di energia, di materia; gravità, elettricità, magnetismo, calore, termodinamica, teorie atomiche, probabilità, tutto passa sotto il suo vaglio critico. E le Memorie originali che nel frattempo accompagnano i corsi, vengono spesso seguite da conferenze e articoli divulgativi, destinati a pubblicizzare le conclusioni dei suoi studi.
Come giustamente sottolinea Darboux [1913, p. 39], fino alla fine della sua vita Poincaré “ha proseguito senza stancarsi il ruolo di regista e di consulente che aveva assunto in fisica teorica”. È datato gennaio 1912 uno dei suoi articoli dedicato alla teoria quantistica di Planck, che era stata oggetto di discussione nella prima Conferenza Solvay sulla fisica, tenutasi a Bruxelles dal 30 ottobre al 3 novembre dell'anno precedente.
Ma vi sono altri campi importantissimi in cui Poincaré ha lasciato orme indelebili. Il primo è quello della Topologia algebrica. Il secondo è quello della Meccanica celeste in cui Poincaré, a partire dal 1890, comincia a riprendere e sviluppare le scoperte che gli avevano meritato il brillante successo del 1889. È così che pubblica nel 1892-93 i primi due volumi della grande opera: Les méthodes nouvelles de la mécanique céleste [I nuovi metodi della meccanica celeste], che costituisce appunto lo sviluppo della Memoria premiata con la medaglia del re di Svezia. Non meraviglia perciò che nel 1896 gli venga offerta la cattedra di Astronomia matematica alla Sorbona già occupata da Félix Tisserand (1845-1896). Sulla nuova cattedra Poincaré completa il suo grande lavoro sui nuovi metodi della meccanica celeste, pubblicando il terzo volume nel 1899. Ma ne aveva già iniziato un altro, più pratico: le Lezioni di meccanica celeste, in tre volumi, apparse tra il 1905 e il 1910. Infine, Poincaré lasciò pubblicare dai suoi studenti due corsi di grande interesse: Sulle figure di equilibrio di una massa fluida (1902), e Sulle ipotesi cosmologiche (1911).
Completiamo questa carrellata dell'attività scientifica di Poincaré, necessariamente molto sommaria, con l'accennare alle sue incursioni nel campo delle geometrie non euclidee che abbiamo già incontrato all'inizio di questa narrazione nel ricordare le sue ricerche sulle funzioni fuchsiane. Si tratta di riflessioni che costituiscono per altro la porta d'ingresso ai suoi lavori epistemologici, oggetto del saggio di Polizzi. Per brevità, accenneremo solo al modello di Poincaré, presentandolo con le sue stesse parole. Partendo – sulla scorta di Klein – dalle ricerche di Cayley, così Poincaré presenta il suo modello:
| Supponiamo, scrive, di avere un mondo racchiuso in una sfera di grandi dimensioni e sottomessa alle leggi seguenti:
La temperatura non è uniforme: è maggiore al centro e diminuisce man mano che ci si allontana da esso, per ridursi a zero quando si raggiunge la sfera in cui questo mondo è racchiuso. Si può precisare meglio la legge con di variazione della temperatura. Sia R il raggio della sfera limite, ed r la distanza del punto considerato dal centro della sfera. La temperatura assoluta è proporzionale a R2 – r2. Si assuma inoltre che, in questo mondo, tutti i corpi abbiano lo stesso coefficiente di dilatazione, in modo che la lunghezza di qualsiasi regolo sia proporzionale alla temperatura assoluta. Si supponga, infine, che un oggetto trasportato da un punto ad un altro dove la temperatura è diversa, si metta immediatamente in equilibrio termico con il suo nuovo ambiente. Nulla in queste ipotesi è contradditorio o incredibile. Un oggetto mobile diverrà sempre più piccolo man mano ci si avvicina alla sfera limite. Si osservi in primo luogo che se questo mondo è limitato dal punto di vista della nostra geometria abituale, sembrerà infinito ai suoi abitanti. Quando questi, in effetti, desiderano effettivamente avvicinarsi alla sfera limite, si raffreddano e diventano sempre più piccoli. I passi che fanno vanno diventando sempre più piccoli, in modo che non potranno mai raggiungere la sfera limite. Si faccia ancora un'altra ipotesi, che la luce attraversi dei mezzi diversamente rifrangenti, e in modo che l'indice di rifrazione sia inversamente proporzionale a R2 – r2. È facile vedere che, in queste condizioni, i raggi di luce non sono rettilinei, ma circolari. |
Nell'ambiente ideato da Poincaré, gli esseri fittizi di cui si parla, se facessero della geometria, adotterebbero la geometria non euclidea. Le linee rette, i raggi luminosi della geometria ordinaria, sarebbero sostituiti da cerchi ortogonali alla sfera limite, ed i piani da sfere ortogonali alla sfera stessa.
È certamente impressionante, oltre la varietà dei campi di studio affrontati da Poincaré, la grande ampiezza dei suoi scritti a fronte di una durata di vita così breve: più di 30 volumi e circa 500 fra Note e Memorie sparse nelle riviste di tutto il mondo. Com'è naturale, tante pubblicazioni brillanti su argomenti così diversi ne avevano diffuso la fama in tutto il mondo. Egli apparteneva a vario titolo ad una quarantina di accademie o società scientifiche, francesi e straniere. Era dottore h.c. delle Università di Cambridge, Christiania, Kolozsvàr, Oxford, Glasgow, Bruxelles, Stoccolma, Berlino. La Royal Astronomical Society gli aveva conferito nel 1900 la medaglia d'oro, e un anno dopo era la Royal Society a conferirgli la medaglia Sylvester. Nel 1904 riceveva la Medaglia d'Oro Lobatschevski della Società fisico-matematica di Kazan. Nel 1905, su proposta di una Commissione internazionale, l'Accademia Ungherese delle Scienze gli assegnava il Gran Premio Bolyai, appena fondato in onore dei due illustri studiosi, Farkas (padre) e János (figlio). Naturalmente lasciamo immaginare quelli ricevuti in patria, ricordando solo la sua nomina, nel 1908, ad accademico di Francia al posto lasciato libero dal grande poeta Sully Prudhomme (1839-1907). Tutti questi onori testimoniano l'ammirazione e la stima che i suoi colleghi e i suoi pari avevano per lui, ma va detto che le opere filosofiche pubblicate a partire dal 1902 gli valsero una popolarità sconosciuta a qualsiasi altro scienziato francese.
Numerose anche le partecipazioni ai congressi, in Francia e all'estero. Nel 1900, in concomitanza con l'Esposizione di Parigi, Poincaré tenne tre conferenze nel giro di una quindicina di giorni: l'11 agosto, Sul ruolo dell'intuizione e della logica in matematica, al secondo Congresso internazionale di matematici, di cui era stato eletto presidente; il secondo Sui princìpi della meccanica, al Congresso internazionale di Filosofia, e il terzo, infine, Sulle relazioni della Fisica sperimentale e della Fisica matematica, al contemporaneo Congresso internazionale dei fisici. Nel 1904, partecipò al Congresso internazionale di Arte e Scienza tenutosi a Saint Louis, durante l'Esposizione Universale per celebrare il centenario della riunione della Louisiana agli Stati Uniti. Il 24 settembre vi lesse una conferenza dal titolo: Lo stato presente e il futuro della Fisica matematica. Come comunicava in una lettera del 30 luglio 1904 a Giovan Battista Guccia (1854-1914), sarebbe partito il 6 agosto e contava di profittare dell'occasione per visitare diverse regioni degli Stati Uniti.
Potremmo continuare, ma preferiamo avviarci alle conclusioni con un rapido cenno alla famiglia di Henri Poincaré.
Il 20 aprile 1881 aveva sposato Louise Poulain d'Andecy e dal matrimonio erano nati quattro figli: Jeanne, il 3 giugno 1887; Yvonne, il 9 novembre 1889; Henriette, il 18 gennaio 1891; e, infine, il tanto atteso figlio maschio, Léon Maurice, l'1 giugno 1893. Apparteneva per il ramo materno a una famiglia di scienziati, i Geoffroy Saint-Hilaire, “ed anche se non l'avesse trovato nel suo affetto e nella sua grande intelligenza, Madame Poincaré aveva ricevuto dalla sua famiglia l'idea della vita che avrebbe dovuto circondare uno studioso come il marito. Le sue tre figlie e il figlio si univano a lei nel dare al padre tutto il loro affetto, e tutta la soddisfazione possibile; il cognato e la sorella, i coniugi Boutroux, suo nipote Pierre Boutroux, il suo cugino Raymond Poincaré, Lucien Poincaré, hanno avuto con lui rapporti i più affettuosi e i più stretti. I suoi colleghi, felici di stare a fianco di un uomo di genio, gli mostravano fiducia e rispetto, qualità cui era molto sensibile. Sebbene egli non facesse nulla per imporre i suoi pareri, le sue opinioni erano per noi una grande autorità” [Darboux 1913, p. 62].
Sembrava in sostanza che la vecchiaia sarebbe arrivata felice, insieme agli onori e alla certezza di aver contribuito ad accrescere il patrimonio morale del suo paese con l'esempio di una vita instancabilmente spesa nei lavori più nobili. Il destino aveva disposto diversamente.
2. Il “cervello vivente delle scienze razionali” si è spento
Il 17 luglio 1912 il parigino Le Temps pubblicava un articolo di Paul Painlevé (1863-1933) con la notizia dell'improvvisa morte di Henri Poincaré avvenuta nella mattinata. “Oggi – scriveva il matematico – su tutta la faccia della terra, alcune migliaia di scienziati, di ricercatori, di ingegneri che proseguono la lotta eterna della nostra specie contro il mistero, contro l'ignoto, contro la materia ribelle, accoglieranno la notizia di questa morte come un lutto personale, come una diminuzione delle forze dell'umanità. E aggiungeva:
| Henri Poincaré era veramente il cervello vivente delle scienze razionali. Matematica, astronomia, fisica, cosmogonia, geodesia, tutto egli ha abbracciato, tutto ha penetrato, tutto ha approfondito. Inventore incomparabile, non si è limitato a seguire le sue aspirazioni, ad aprire vie inattese, a scoprire nell'universo astratto della matematica molta “terra ignota”. Ovunque la ragione di un uomo ha saputo insinuarsi, che si trattasse di telegrafia senza fili, di fenomeni radiologici o della nascita della terra, Henri Poincaré si è posto al suo fianco per aiutare e prolungare le sue ricerche, per seguire quel filone prezioso. Sforzo diversamente meraviglioso da quello dell'enciclopedista, la cui memoria potente si limita a registrare dei fatti di comprensione immediata.
Con il grande matematico francese scompare dunque il solo uomo il cui pensiero fosse capace di trattenere in sé tutti gli altri pensieri, di comprendere fino in fondo, e con una specie di scoperta rinnovata, tutto ciò che il pensiero umano può comprendere oggi. È per questo che la sua scomparsa prematura, nel pieno vigore intellettuale, è un disastro. Delle scoperte saranno ritardate, dei tentennamenti si prolungheranno, perché il cervello potente e luminoso non sarà più lì a collegare ricerche che si ignorano, o a gettare, nel mondo dei fatti oscuri bruscamente rivelati dall'esperienza, l'ardito colpo di sonda di una nuova teoria. |
Poincaré è morto per i postumi di un intervento chirurgico alla prostata, una malattia che si era manifestata improvvisa durante i lavori del Congresso internazionale dei matematici in Roma (6-11 aprile 1908), e gli aveva impedito persino di leggere l'attesa conferenza su “L'Avvenire della Matematica”. Nei mesi e negli anni successivi, la malattia l'aveva continuato a perseguitare come si apprende da una lettera a Hilbert (del febbraio-marzo 1909), con la quale Poincaré preparava il viaggio a Göttingen (dal 22 al 29 aprile 1909): «C’è ora un punto sul quale desidero richiamare la sua attenzione. Sono ancora sotto il colpo del malore che mi ha colpito l’anno scorso a Roma e sono imperiosamente obbligato a usare certe precauzioni. Io non posso bere né vino né birra, ma solo acqua. Non posso assistere a un banchetto né ad un pasto prolungato».
Comunque, la malattia non aveva impedito a Poincaré la sua attività scientifica, continuando ad occuparsi in particolare del problema dei tre corpi. Ma, alla fine del 1911, scrisse una lettera all'amico Giovan Battista Guccia (1855-1914), direttore e fondatore di quel “Circolo Matematico di Palermo” che sui propri Rendiconti aveva pubblicato alcune delle sue Memorie più belle, nella quale vi è un passo che lascia sospettare la consapevolezza che la malattia non lo lasciava tranquillo. Ecco la lettera, giustamente famosa:
| Caro Amico,
Le ho parlato durante la sua ultima visita di un lavoro che mi occupa da due anni. Io non sono andato molto avanti, e ho deciso di abbandonarlo temporaneamente per dargli il tempo di maturare. Ciò andrebbe bene se fossi sicuro di poterlo riprendere; alla mia età non posso risponderne, ed i risultati ottenuti, suscettibili di mettere i ricercatori su una via nuova e inesplorata, mi sembrano troppo promettenti, nonostante le delusioni che mi hanno causato, perché io mi rassegni a sacrificarli. In queste condizioni, troverebbe lei conveniente pubblicare una Memoria incompiuta, dove io esporrei l'obiettivo che ho perseguito, il problema che ho proposto, ed i risultati dei miei sforzi per risolverlo? Questo sarebbe un po' inusuale, ma forse potrebbe essere utile. Ciò che mi lascia perplesso è che dovrò mettere molte figure, proprio perché non sono riuscito a pervenire ad una regola generale, ma ho solo accumulato soluzioni particolari. Mi dica, per favore, cosa ne pensa di questa questione e cosa mi consiglia. Il suo amico devoto, Poincaré. |
Come è facile prevedere, Guccia si affrettò a richiedere la Memoria che gli era stata proposta. Un lavoro che ad un geometra come Poincaré era apparso meritevole di sforzi prolungatisi per oltre due anni era una fortuna da non rifiutare. Il lavoro [Poincaré 1912b] è dunque apparso poco prima della morte. Come scrive Darboux [1913, p. 65], “la dimostrazione completa, se Poincaré fosse stato in grado di farla, avrebbe permesso ad esempio di stabilire l'esistenza di un numero illimitato di soluzioni periodiche in un caso del problema dei tre corpi più generale di quelli che aveva precedentemente considerato fino ad allora”.

Giovan Battista Guccia
L'anno 1912 era stato denso di viaggi, a Londra, a Vienna e a Bruxelles, e ancora il 26 giugno, a tre settimane dalla morte, Poincaré aveva tenuto un discorso alla “Ligue française d'éducation morale” a cui aveva accettato di aderire. Subito dopo, la situazione era precipitata ed i medici decisero l'intervento, poi effettuato il 9 luglio. L'intervento sembrava riuscito e buona la ripresa post-operatoria, stando almeno alle notizie che la famiglia dava a Darboux. Ma “un accident imprévu, une embolie sans doute, est venu, le 17 juillet, tromper toutes nos espérances”. E Darboux [1913, p. 66] aggiunge:
| In appena un quarto d'ora la morte ci ha tolto colui che consideravamo come salvato definitivamente. Quando la funesta notizia ci venne annunziata, restammo a lungo senza credervi. […] Si può ripetere ora ciò che Poincaré stesso ha detto per la morte di Curie. Non v'era francese, per quanto ignorante, che non sentisse più o meno confusamente quale forza la Patria e l'Umanità avessero perduto. |
Ci piace concludere con le parole che Poincaré ha pronunziato in occasione della laurea honoris causa conferitagli dall'Università libera di Bruxelles in occasione dei festeggiamenti per il 75° anniversario della fondazione:
| La libertà è per la Scienza ciò che l'aria è per l'animale; privata di questa libertà, muore per soffocamento, come un uccello privato dell'ossigeno. E questa libertà deve essere illimitata, in quanto, se si volessero imporle limiti, si otterrebbe solo una mezza scienza, e mezza scienza non è più scienza, perché può essere, anzi è necessariamente, una scienza falsa. Il pensiero non deve mai essere subordinato a qualsiasi dogma, partito politico, passioni, interessi, idee precostituite, a tutto perciò, tranne che ai fatti stessi, perché, per la scienza, essere subordinata significa morire. |
Note
1. Per la stesura di questa parte mi sono giovato dei seguenti saggi: [Darboux, 1913], [Appell 1925], [Severi 1949] e [Bottazzini 1999].
2. Cfr. [Dugac 1984, p. 150].
3. Sul'influenza di Boutroux su Poincaré si veda [Nye 1979].
4. In quell'anno, infatti, Gabriel Lippmann (1845-1921), veniva nominato docente di fisica alla Sorbona e direttore dei relativi laboratori.
5. Manifestando un primo interesse al problema dei tre corpi con l'articolo [Poincaré 1884].
6. La Memoria presentata da Poincaré fu pubblicata postuma in [Poincaré 1923]. Cfr. H. Poincaré, Extrait d'un mémoire inedit de H. P. sur les fonctions fuchsiennes, Acta Mathematica, 39 (1923), pp. 58-93.
7. L'equivalente locuzione francese «Qui s'y frotte s'y pique» si potrebbe tradurre come «Chi mi tocca si scotta», ma è preferibile quella data nel testo.
8. Lazarus Fuchs (1833-1902).
9. Si veda [Poincaré 1908b].
10. Cito da [Poincaré 1989], pp. 39-40.
11. Cfr. [Poincarè 1921, pp. 95-100].
12. Si veda [Poincaré 1907]. Contemporaneamente, anche un giovane matematico tedesco, Paul Koebe (1882-1945), era arrivato alla risoluzione del problema dell'uniformizzazione, la cui importanza era stata sottolineata da Hilbert che l'aveva inserito nella lista dei 23 problemi presentata al Congresso internazionale dei matematici di Parigi (1900). Sul problema si veda [Gray 2008, Appendix 5 (“Uniformisation Theorem”), pp. 261-266].
13. Victor Puiseux (1820-1883); Joseph Alfred Serret (1819-1885); Jean-Claude Bouguet (1819-1885).
14. Edmond Laguerre (1834-1886).
15. Per una storia del premio si veda [Barrow-Green 1997] e [Nabonnand 1999].
16. Le proposte della Commissione furono pubblicate negli Acta Mathenatica (7, 1885-86, pp. I-VI). I primi due temi erano stati proposti da Weierstrass, i rimanenti da Hermite.
17. Intégration des équations différentielles au moyen de fonctions elliptiques, Journal de l'École Polytechnique, 21 (1856), pp. 199–254.
18. Cfr. [Poincaré 1890].
19. [Nabonnand 1999, p. 177.
20. Ibidem, p. 178, lettere del 17 e 22 ottobre1888.
21. Solo di questo corso è stata fatta una riedizione riveduta e ampliata dallo stesso Poincaré (Gauthier-Villars, Paris, 1912).
22. Cfr. [Poincaré 1912].
23. Come scrisse Solomon Lefschetz (1884-1972), «Forse in nessun altro ramo della matematica Poincaré pose la sua impronta più indelebile che sulla Topologia» [Lefschetz 1930, “Preface”, p. V].
24. Cfr. [Poincaré 1904, p. 258]. Per maggiori dettagli si veda [Bottazzini 1999, in particolare le pp. 49-57].
25. L'articolo è riprodotto nel volume 38 (1921) di Acta Mathematica (pp. 399-402).
26. Per il ruolo di Poincaré nel Congresso e le vicende della malattia (per la quale fu ottimamente assistito soprattutto dagli amici Guccia e Volterra) si veda [Guerraggio e Nastasi 2008], dove si può leggere (Appendice II, pp. 178-198) il testo della conferenza.
27. Si veda [Nabonnand 1999, p. 349].
28. La lettera, del 9 dicembre 1911 [data del timbro postale], è trascritta in [Darboux 1913, p. 64] e pubblicata in fac-simile nel Supplemento ai Rendiconti del Circolo Matematico di Palermo, vol. 8 (1913), pp. 28-29.
29. George David Birkhoff (1884-1944) riuscì a darne una brillante dimostrazione, in [Birkhoff 1913], subito dopo la pubblicazione palermitana dell'“ultimo teorema”.
30. Pierre Curie (1859-1906), Premio Nobel per la fisica nel 1903, era stato ucciso da una carrozza in Place Dauphine.
31. Cfr. [Poincaré 1909, p. 5] e [Mawhin 2005, p. 1043].
Riferimenti bibliografici
[Appell 1925] P. Appell, Henri Poincaré, Plon, Paris, 1925.
[Barrow Green 1997] J. Barrow Green, Poincaré and the Three Body Problem (Amer. Math. Soc. / London Math. Soc., Providence (R. I.), 1997.
[Birkhoff 1913] G.D. Birkhoff, Proof of Poincaré's Geometric Theorem, Transactions of Amer. Math. Soc., vol. 14, 1 (1913), pp. 14-22.
[Bottazzini 1999] U. Bottazzini, Poincaré il cervello delle scienze razionali, Le Scienze, Milano, 1999.
[Darboux 1913] G. Darboux, Eloge Historique d'Henri Poincaré, membre de l'Académie, Oeuvres de Henri Poincaré, tome II, Gauthier-Villars, Paris, 1916, 11 voll., II, pp. 7-71.
[Dugac 1984] P. Dugac (a cura di), Lettres de Charles Hermite à Gösta Mittag-Leffler (1874-1883), Cahiers du séminaire d'histoire des mathématiques, 5 (1984), pp. 49-285.
[Gray 2008] J. J. Gray, Linear Differential Equations and Group Theory from Riemann to Poincaré, Birkäuser, Boston, 2008 (seconda edizione ampliata rispetto alla prima del 1999).
[Guerraggio e Nastasi 2008] A. Guerraggio e P. Nastasi, Roma 1908: il congresso internazionale dei matematici, Boringhieri, Torino, 2008.
[Hermite 1881] C. Hermite, Rapport sur le grand prix des sciences mathématiques 1881, Comptes Rendus, 92 (1881), pp. 553-54.
[Lefschetz 1930] S. Lefschetz, Topology, Amer. Math. Soc., New York, 1930.
[Mawhin 2005] J. Mawhin, Henri Poincaré. A Life in the Service of Science, Notices of AMS, vol. 52, 9 (2005), pp. 1035-1044.
[Nabonnand 1999], Ph. Nabonnand (a cura di), La correspondance entre Henri Poincaré et Gösta Mittag-Leffler, Birkhäuser, Basel, 1999.
[Nye 1979] M.J. Nye, The Boutroux Circle and Poincaré's Conventionalism, Journal of History of Idea, 40 (1979), n. 1, pp. 107-120.
[Poincaré 1878] H. Poincaré, Notes sur les propriétés des fonctions définies par les équations différentielles, Journal de l'École Polytechnique, vol. 45 (1878), pp. 13-26.
[Poincaré 1879] H. Poincaré, Sur les propriétés des fonctions définies par les équations aux différences partielles, Thèse pésentée à la Faculté des Sciences de Paris, 1er août 1879, Gauthier-Villars, 1879.
[Poincaré 1881] H. Poincaré, Mémoire sur les courbes définies par une équation différentielle, Journal de Mathématiques pures et appliquées, (3) 7 (1881), pp. 375-422.
[Poincaré 1882 a] H. Poincaré, Théorie des groupes fuchsiens, Acta Mathematica, 1 (1882), pp. 1-62.
[Poincaré 1882 b] H. Poincaré, Sur les fonctions fuchsiennes, Acta Mathematica, 1 (1882), pp. 193-294.
[Poincaré 1883a] H. Poincaré, Un théorème de Riemann relatif aux fonctions de n variables indépendantes admettant 2n systèmes de périodes (en collaboration avec Émile Picard), Comptes rendus rendus hebdomadaires de l'Acad. des sci., 97 (1883), pp. 1284-1287.
[Poincaré 1883b] H. Poincaré, Sur un théorème de la théorie générale des fonctions, Bulletin de la société mathématique de France, 11 (1883), pp. 112-125.
[Poincaré 1884] H. Poincaré, Sur certaines solutions particulières du problème des trois corps, Bullettin astronomique, 1 (1884), pp. 65-74.
[Poincaré 1890] H. Poincaré, Sur le problème des trois corps et les équations de la dynamique, Acta Mathenatica, 13 (1890), pp. 1-270.
[Poincaré 1902] H. Poincaré, La Science et l'hypothèse, Flammarion, Paris, 1902
[Poincaré 1904] H. Poincaré, Wissenschaft und Hypothese, Teubner, Leipzig, 1904 (trad. tedesca, a cura di F. Lindemann, di [Poincaré 1902].
[Poincaré 1907] H. Poincaré, Sur l'uniformisation des fonctions analytiques, in Acta Mathematica, 31 (1908), pp. 1-63 [la prima pagina del lavoro porta la scritta: «Imprimé le 19 mars 1907». E in effetti il volume 31 doveva uscire alla fine del 1907. Uscì invece all'inizio del 1908, probabilmente per la morte del re Oscar II avvenuta proprio in dicembre].
[Poincaré 1908a] H. Poincaré, Science et Méthode, Flammarion, Paris, 1908); trad. it. a cura di Claudio Bartocci, Scienza e Metodo, Einaudi, Torino,1997.
[Poincaré 1908b] H. Poincaré, L'invention mathématique, Enseignement mathématique, 10 (1908), pp. 357-371.
[Poincaré 1909] H. Poincaré, Le Libre Examen en matière scientifique, Conférence faite aux Fêtes jubilaires de l'Université de Bruxelles, le 21 novembre 1909, Imprimerie La Meuse, Liège, 1909
[Poincaré 1912a] H. Poincaré, Sur la théorie des quanta, Journal de physique et le radium, 2 (1912), pp. 5-34.
[Poincaré 1912b] H. Poincaré, Sur un théorème de géométrie, Rendiconti Circolo Matematico di Palermo, (1) 33 (1912), pp. 375-407.
[Poincaré 1921] H. Poincaré, Analyse de ses travaux scientifiques, Acta Mathematica, 38 (1921), pp. 3-135.
[Poincaré 1923] H. Poincaré, Extrait d'un mémoire inedit de Henri Poincaré sur les fonctions fuchsiennes, Acta Mathematica, 39 (1923), pp. 58-93.
[Poincaré 1989], H. Poincaré, Opere epistemologiche, Piovan, Abano Terme, 1989 (a cura di G. Boniolo).
[Severi 1949] F. Severi, Poincaré, L'arco, Firenze, 1949.