Il miracolo di Morley e altre regolarità dei triangoli
Introduzione
Uno dei risultati più sorprendenti di geometria elementare, nei tempi moderni, fu enunciato nel 1899 da Frank Morley (1860 - 1937) e comparve come caso particolare di un altro teorema nel primo volume delle Transactions of the American Mathematical Society. Subito la proprietà si diffuse e cominciò a circolare, non indisturbata, fra la curiosità dei matematici interessati alla "geometria del triangolo", finché, secondo Coxeter [2], fu finalmente dimostrata con metodi elementari daW.E. Philip nel 1914.
In seguito la dimostrazione conobbe ulteriori versioni e, per la sua singolarità, all'interno della comunità matematica la proprietà meritò l'appellativo di "miracolo di Morley". Un fatto di "folklore matematico" che suscitò gli interessi di molti, come dimostra la quantità di pubblicazioni citate da Oakley e Baker [3] fino al 1978, proseguite in seguito con non minore intensità.
Si tratta di un teorema che presenta in qualche senso una forma di aspirazione alla regolarità da parte dei triangoli. Come numerosi altri risultati di questo campo di studi, non occorrono strane ipotesi o artificiose costruzioni: si eseguono alcuni semplici passaggi a partire da un triangolo qualsiasi ed ecco ... rimane definito un triangolo equilatero. L'enunciato è chiaro fin dall'inizio e comprensibile a tutti:
Teorema di Morley. In un triangolo si trisechino gli angoli interni. I tre punti di intersezione delle trisecanti adiacenti formano un triangolo equilatero.
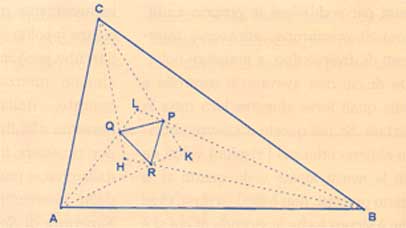
Figura 1
In altre parole, con riferimento alla figura 1, ogni triangolo ABC contiene dentro di sé un triangolo equilatero costruito prendendo le trisecanti AQ ed AR dell'angolo in A, e BR dell'angolo in B e CP e CQ dell'angolo in C. Il triangolo di Morley, che ha per vertici le intersezioni P, Q ed R delle trisecanti adiacenti, è sempre equilatero.
Alcune delle numerose dimostrazioni di questa proprietà sono "dirette", di natura trigonometrica (come quella di A. Letac, del 1939, citata nel sito www.cut-the-knot.com, per l'appunto sotto Morley's miracle). Altre, come ad esempio quella di Coxeter [2], o quella "costruttiva" di Conway (anch'essa reperibile nel sito citato), procedono "all'inverso" ed in generale risultano più semplici (anche se non per questo forniscono una migliore spiegazione del "miracolo"): a partire da un triangolo equilatero, costruiscono un altro triangolo che, alla fine, si può rendere simile ad un triangolo qualsiasi (e il triangolo equilatero di partenza costituisce il suo triangolo di Morley).
Con riferimento sempre alla Figura 1, se si intersecano le trisecanti non adiacenti si ottiene un altro triangolo HKL che non è necessariamente equilatero. Tuttavia, una dimostrazione diretta del teorema di Morley si ottiene confrontando, o meglio collegando, i due triangoli PQR e HKL e -cosa ancora più sorprendente per un enunciato di carattere altamente metrico come quello del teorema- si può far dipendere in larga parte da una proprietà proiettiva. È proprio questo tipo di generalità che permette di comprendere nello stesso ambito altre proprietà analoghe, come ad esempio quella nota come teorema di Napoleone (si veda la Figura 2).
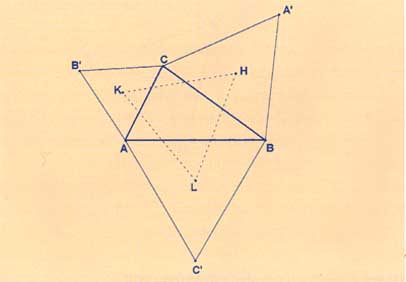
Figura 2
Teorema di Napoleone. In un triangolo, si costruiscano i triangoli equilateri sui lati, esternamente ai lati stessi. I centri di questi triangoli equilateri costituiscono i vertici di un triangolo equilatero.
Una variante del teorema di Napoleone permette di prendere i triangoli equilateri internamente ai lati. Una sua generalizzazione permette di sostituire i triangoli equilateri con triangoli simili, opportunamente disposti.
1. Una proprietà proiettiva dei triangoli
Sul Mathematical Intelligencer del 1996 [4], in relazione al "triangolo di Napoleone", vale a dire al triangolo della figura 2, David Gale segnala la seguente proprietà (figura 3):
Figura 3
Siano p, q ed r tre rette concorrenti del triangolo ABC, uscenti rispettivamente da A, da B e da C. Se FA denota il fascio delle rette passanti per A, sia τA la proiettività di FA in se stesso (univocamente definita) che scambia fra di loro le rette AB ed AC e lascia fissa la retta p. Analogamente si definiscano i fasci di rette FB e FC e le proiettività τB e τC.
Assegnate tre coppie di rette corrispondenti (una per ciascuna proiettività): a e a'=τA(a), b e b'=τB(b) e c e c'=τC(c), si considerano i punti di intersezione A'=b'∩ c, B'=c'∩ a e C'=a'∩ c. Allora le rette AA', BB' e CC' sono concorrenti.
La natura dell'enunciato permette (o meglio "impone") la dimostrazione analitica assumendo il triangolo come riferimento proiettivo e il punto di concorrenza delle tre rette p, q ed r come punto unitario. Così, posto, A(0,1,0), B(1,0,0) e C(0,0,1), le rette di FA hanno equazione x1=h3 e un semplice calcolo mostra che la proiettività si rappresenta con la forma bilineare hh'=1. Inoltre, le rette di FA hanno equazione x2=kx3 e si rappresenta nella forma kk'=1, le rette di FC hanno equazione x2=mx1 e la corrispondente proiettività ha la forma mm'=1.
Ora si ha:
A'=(1,m,km)
B'=(hm,h,m)
C'=(1,hk,h)
e le rette interessate hanno equazioni:
AA'kmx1=x3
BB'mx2=hx3
CC'x2=hkx1
È facile verificare che sono concorrenti.
Il lettore avrà osservato che, in quest'ultima proprietà, le ipotesi sono più ricche di quanto venga utilizzato: di fatto, le proiettività τA, τB e τCsono simmetriche (sono involuzioni) e quindi rimane definito anche un triangolo A''=b∩c, B''=c∩a e C''=a∩b.
In maniera analoga a prima si ricavano le coordinate di questi punti:
A''=(km,k,1)
B'=(1,m,h)
C'=(hk,1,k)
e poi le equazioni delle rette:
AA''x1=kmx3
BB''hx2=mx3
CC''hkx2=x1
che, ovviamente, risultano ancora concorrenti. Ma c'è di più:
Teorema. Con riferimento alle notazioni precedenti, le rette AA' ed AA'' si corrispondono nella proiettività τA . Analogamente le rette BB' e BB'' si corrispondono nella proiettività , così come CC' e CC'' si corrispondono nella proiettività . Inoltre le rette A'A'', B'B'' e C'C'' sono concorrenti.
La prima parte di questa dimostrazione è solo una verifica, la seconda parte si riduce ad un conto -lungo ma senza difficoltà- a partire dalle equazioni delle rette interessate A'A'', B'B'' e CC'':
m(1-k2)x1+(k2m2-1)x2+k(1-m2)x3=0
(m2-h2)x1+m(h2-1)x2+h(1-m2)x3=0
h(1-k2)x1+k(1-h2)x2+(k2h2-1)x3=0
Non rimane che applicare queste proprietà ai teoremi di regolarità.
2. Dimostrazione del teorema di Morley
La figura 1 presenta il triangolo di Morley PQR, ottenuto dalle trisezioni degli angoli interni in A, in B ed in C. Il collegamento con le proprietà proiettive viste in precedenza è il seguente: al posto delle rette concorrenti p, q ed r che là compaiono, si considerano le bisettrici degli angoli interni del triangolo, e trisecanti di ciascun angolo sono allora rette che si corrispondono nelle involuzioni τA, τB e τC oltre al triangolo PQR, rimane definito anche il triangolo HKL. Inoltre, le rette PH, QK e RL sono concorrenti (diciamo O il loro punto comune).
Altre circostanze fondamentali intervengono come "contributo metrico" indispensabile alla dimostrazione. La prima dipende direttamente dalla costruzione, in particolare dal fatto che gli angoli vengono trisecati. La situazione, per quanto riguarda il triangolo di Morley PQR ed il triangolo HKL che è associato, è riassunta nell'esagono della figura 4.
Figura 4
Il punto P è l'incentro del triangolo BHC. Analogamente, Q è l'incentro del triangolo AKC e R è l'incentro del triangolo ALB.
Come conseguenza, la retta HP biseca l'angolo BCH, così come la retta KQ biseca l'angolo AKC e la retta LR biseca l'angolo ALB.
Posto 2δA=RHQ, si ha BPC=90° + δA perché P è l'incentro di BHC e, ancora dal triangolo BPC, si ottiene δA = 90° - 1/3(B+C). Ma anche, se a, b e sono gli angoli segnati nella figura 4 (che compaiono per costruzione), dal triangolo ARQ risulta 2δA=1/3A+b+c . Uguagliando queste quantità si ottiene b+c=120°-1/3(B+C). Analoghi conti valgono per gli altri angoli db e dc definiti in K ed L in maniera analoga a δA. Complessivamente:
b+c=120°-(B+C)/3
a+b=120°-(A+B)/3
a+c=120°-(A+C)/3
Risolvendo rispetto ad a, b e c si ottiene:
a=60°-A/3
b=60°-B/3
c=60°-C/3
In particolare: a+b+c=120°. Si osservi che vale inoltre:
BCP=180°-a
e analogamente per gli altri angoli.
Si può ora calcolare l'angolo KOL, come differenza di angoli del quadrilatero KOLP:
KOL= 360°-OKP-KPL-PLO=360°-(90°-b)-(180°-a)-(90°-c)=120°
Dunque, la configurazione delle tre rette passanti per O vede HOK=KOL=LOK=120° e si conclude subito che i sei "spicchi" nei quali queste rette dividono l'angolo in O, sono ciascuno di 60°. Da qui si ha facilmente che i triangoli RHQ, QLP e PKR sono isosceli, con angoli alla base, rispettivamente, a, b e c e pertanto gli angoli interni del triangolo di Morley valgono, ciascuno, 60°.
3. Altre regolarità
Il cosiddetto teorema di Napoleone è forse una delle proprietà che più spesso di altre vengono riscoperte in matematica. L'attribuzione non è chiara, anche se tutti concordano sul fatto che Napoleone fosse dotato per il ragionamento matematico, interessato alla materia ed amico di numerosi matematici del tempo (Monge, Lagrange, Laplace, Fourier...) In [5], Wetzel cita dal testo noto e ampiamente adottato di Faifofer [6]: "teorema proposto per la dimostrazione da Napoleone a Lagrange".
Figura 5
Una dimostrazione elementare del teorema lo collega a un punto notevole del triangolo dato ABC (nel quale supponiamo che non ci sia un angolo maggiore o uguale a 120°). Il legame fra questo punto F e il triangolo di Napoleone permette di comprendere l'argomento in maniera unitaria e capire le interdipendenze fra le proprietà: F risulta dalla intersezione dei segmenti AA', BB' e CC' che uniscono ciascun vertice del triangolo dato col vertice del triangolo equilatero costruito sul lato opposto (si veda la figura 5).
Come si dimostra che questi tre segmenti sono concorrenti? Questa è ancora una conseguenza della proprietà "proiettiva" del §1: due rette passanti per un vertice di un triangolo si dicono isogonali rispetto a quel vertice se formano angoli uguali con la bisettrice interna. È chiaro che rette isogonali si corrispondono nella proiettività definita nel fascio di rette per quel vertice (le proiettività τA, o τB o τC del §1, quando si consideri fissa la bisettrice interna e corrispondenti i lati del triangolo). Con riferimento alla figura 6, si ha in generale:
Figura 6
Se AB' e AC' sono isogonali rispetto al vertice A e, analogamente, BA' e BC' sono isogonali rispetto a B e CA', CB' sono isogonali rispetto a C, allora le rette AA', BB' e CC' sono concorrenti.
Per quanto riguarda il teorema di Napoleone, si scelgono i tre angoli tutti uguali a 60°.
Il punto F appena definito riveste un'importanza storica per il fatto di essere il primo punto notevole dei triangoli del periodo moderno, dopo i famosi circocentro, incentro, baricentro e ortocentro, (noti dall'antichità). Si tratta del punto interno al triangolo che - qui interviene la limitazione che non esista in ABC un angolo maggiore o uguale a 120°- minimizza la somma delle distanze dai vertici. Secondo Dörrie [7], il problema di risolvere questo problema di minimo fu posto da Fermat (1601-1665) a Torricelli (1608-1647), il quale fornì numerose soluzioni. Questo punto assume di conseguenza vari nomi: punto di Fermat, o di Torricelli o, in maniera più tecnica, meno compromettente ma anche più banale, primo centro di isogonia.
Come interviene il punto di Fermat - Torricelli nella dimostrazione del teorema di Napoleone? Si comincia a dimostrare (il riferimento è alla figura 5) che si ha:
AA'=BB'=CC'
Inoltre questo valore comune è uguale a AF+BF+CF. Di conseguenza si ha anche:
AFB=AFC=BFC=120°
Figura 7
Per le prime uguaglianze basta osservare che i triangoli ACA' e BCB' sono uguali perché hanno uguali due lati e l'angolo compreso (quello in C). Dunque AA'=BB'. Analogamente AA'=CC'. Che questo valore comune sia uguale alla somma delle distanze di F dai vertici risulta subito (si veda la figura 7, in cui il triangolo B'AH si ottiene ruotando di 60° il triangolo CAF intorno al vertice A): basta tener conto del fatto che i triangoli AFH e ACB' sono equilateri e calcolare gli angoli coinvolti per avere che H appartiene alla retta BB' (a cui appartiene anche il punto F). Inoltre CF=B'H e AF=HF.
In questo modo si ha anche facilmente la proprietà di minimo del punto F di Fermat - Torricelli: infatti se si applica la stessa costruzione precedente in relazione ad un altro punto F' interno al triangolo ABC si ottiene una spezzata B'HF'B che è ovviamente più lunga del segmento BB'.
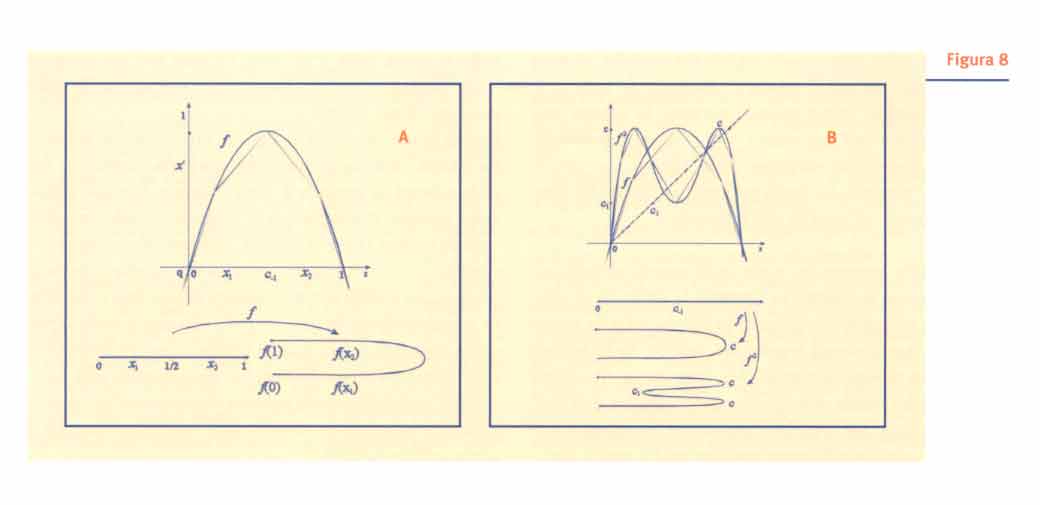
Figura 8
Dalle considerazioni precedenti si ha che il punto F è comune alle tre circonferenze circoscritte ai triangoli equilateri costruiti sui lati di ABC (figura 8). I centri di queste circonferenze sono proprio i vertici del "triangolo di Napoleone" ed i lati di questo triangolo risultano ortogonali agli "assi radicali" FA, FB e FC. Il teorema di Napoleone è ora immediato.
In particolare, si sarà osservato che dalla dimostrazione del teorema di Morley si ha che il triangolo PQR e il triangolo HKL hanno lo stesso punto di Fermat - Torricelli. E questo fatto è risultato rilevante per la dimostrazione.
La configurazione appena ottenuta suggerisce anche che la retta FB' biseca l'angolo CFA (che è di 120°). Così pure FA' biseca BFC e FC' biseca AFB. Si ha la stessa situazione del teorema di Morley: come punto di Fermat - Torricelli, F è comune sia al triangolo ABC che al triangolo A'B'C', inoltre, gli "spicchi" nei quali rimane suddiviso l'angolo giro in F sono tutti di 60°. Di conseguenza, se si itera il procedimento, considerando i triangoli equilateri, esternamente, sui lati di A'B'C', si ottengono tre altri vertici A'', B'' e C'', ciascuno allineato coi punti dai quali ha avuto origine, , e rispettivamente, oltre che con (si veda la figura 9).
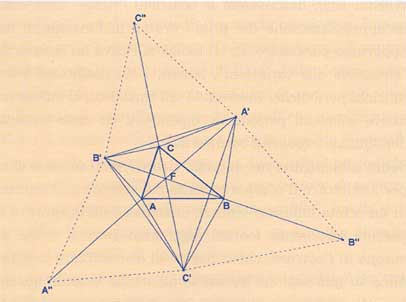
Figura 9
Secondo Wetzel [5], il fatto precedente è all'origine del primo risultato che inverte in qualche senso il teorema di Napoleone. Il senso di questi teoremi inversi è quello di prendere alcuni elementi della costruzione e tentare di determinare l'ambito di variabilità degli altri. In questo caso, il problema consiste nel ritrovare il triangolo ABC partendo dai vertici A', B' e C'. L'elegante soluzione di questo problema, attribuita a Ludwig Kiepert (1846-1934), è molto semplice: dati A', B' e C', i punti A, B e C del triangolo originario sono, rispettivamente, i punti medi dei segmenti A'A'', B'B'' e C'C''. Infatti, con opportune rotazioni di 60°intorno ad A, B e C (del tipo di quella della figura 7) si ricava:
2(FA+FB+FC)=FA'+FB'+FC'
Ma questo non è tutto. Anche una generalizzazione significativa è possibile, poiché il fatto decisivo della dimostrazione del teorema di Napoleone è che le tre circonferenze circoscritte hanno un punto comune. Non importa dunque che i triangoli costruiti sui lati sia equilateri.
Si prendano, esternamente al triangolo dato, tre triangoli simili (costruiti come nella figura 10) ABC', ACB' e BCA' con la proprietà che la somma degli angoli in A', in B' e in C' dia 180°. Si tratta allora di coppie di rette isogonali e dunque, al solito, i segmenti AA', BB' e CC' sono concorrenti.
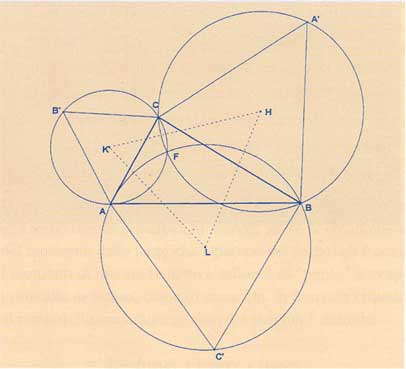
Figura 10
È allora facile verificare che le circonferenze circoscritte a questi triangoli hanno un punto in comune (che generalizza il punto di Fermat - Torricelli). Si applica allora una dimostrazione del tutto analoga a quella del teorema di Napoleone. Si considera il triangolo formato dai circocentri di questi tre triangoli simili: i suoi lati sono ortogonali alle corde comuni e di conseguenza questo triangolo risulta essere simile ai triangoli costruiti sui lati.
Bibliografia
[1] Frank Morley, On the metric geometry of the plane n-line, Trans. Am. Math. Soc. 1 (1900), 97-115.
[2] Harold S.M. Coxeter, Introduction to geometry, John Wiley & Sons, 1961.
[3] Cletus O. Oakley e Justine C. Baker, The Morley trisector theorem, Am. Math. Monthly 85 (1978), 737-745.
[4] David Gale, Mathematical entertainments, The Mathematical Intelligencer 18 (1996), 31-34.
[5] John E. Wetzel, Converses of Napoleon's theorem, Am. Math. Monthly 4 (1992), 339-351.
[6] Aureliano Faifofer, Elementi di geometria, Venezia 1911.
[7]Heinrich Dörrie, Great problems of elementary mathematics, Dover 1965.
