Luci e ombre
Le ombre solari nella storia della scienza
Le ombre sono state sempre importanti nella storia della scienza: molte cono scenze astronomiche sono state rese possibili proprio dall'osservazione delle ombre solari. Tutti ricordano, per averlo letto nei libri di scuola elementare, il famoso aneddoto che ha per protagonista il grande genio dell'età classica,Talete (624- 546 a .c. circa) che riuscì a determinare l'altezza della grande piramide di Cheope, una costruzione che al suo tempo aveva già più di mille anni, proprio osservandone e misurandone l'ombra.

Per chi non ricordasse: Talete, dopo aver conficcato a terra un bastone, attese finché l'ombra del medesimo non fosse stata lunga come il bastone stesso; contemporaneamente, diede l'ordine di segnare sul terreno l'estremo dell'ombra del vertice della piramide. Per la similitudine dei triangoli ABC ed A'B'C'; la lunghezza dell'ombra coincide con l'altezza della tomba del faraone dopo aver aggiunto, ovviamente, la metà della base della piramide stessa.
Un altro straordinario successo scientifico fu la misurazione del raggio terrestre da parte di Eratostene (276- 194 a .c.) il grande filosofo, matematico, storico, geografo e poeta vissuto ad Alessandria d'Egitto. Anche in questo caso, le ombre solari giocarono un ruolo determinante.
Eratostene aveva osservato che a Siene (oggi Assuan) nel giorno del solstizio estivo, a mezzogiorno, anche i pozzi più profondi erano illuminati, ovverosia il sole era perfettamente perpendicolare (Assuan si trova infatti sul tropico del Cancro). Nello stesso giorno ed alla stessa ora, ad Alessandria d'Egitto (quasi sullo stesso meridiano di Siene) un bastone piantato verticalmente gettava invece un'ombra con un angolo di elevazione di un cinquantesimo dell'angolo giro α=360°/50.
Schematizzando la situazione, si nota che vi è una proporzione diretta tra la lunghezza della circonferenza terrestre e la distanza Siene-Alessandria: la lunghezza della circonferenza terrestre è 50 volte lo spazio che separa le due città egiziane. Con le misure dell'epoca, espresse sostanzialmente in giorni di cammino, Eratostene riuscì a stimare (grandissimo risultato!) il raggio terrestre con un errore inferiore al 4%.
Matematica delle ombre solari
Le ombre solari possono essere formalizzate mediante le affinità, in particolare le affinità omologiche. Con il termine affinità, s'intende una trasformazione del piano in sé che ha come invarianti la collineazione ed il parallelismo.
L'esempio più "naturale"di affinità omologica è dato dalla relazione tra un oggetto e la sua ombra. Nel piano cartesiano le affinità si possono tradurre in equazioni lineari:
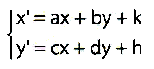
con la condizione che il determinante della matrice dei coefficienti sia diverso da zero:
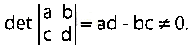
Ad esempio, data la trasformazione:
il quadrato A(1,1) B(4,1) C(4,4) D(1,4) si trasforma nel parallelogramma A'(3,-5) B'(-3,-2) C'(0,-5) D'(6,-8).
Segmenti paralleli si trasformano in segmenti paralleli tra loro, mentre non si mantiene la perpendicolarità, come accade nel fenomeno delle ombre solari.
Le ombre prodotte da una lampada
Osservando le ombre prodotte da una lampada si nota immediatamente che il parallelismo non è un invariante. L'ombra di segmenti verticali non dà sul piano (dell'ombra) segmenti paralleli. Bisogna modificare il modello matematico.

Le trasformazioni geometriche che permettono di formalizzare queste ombre sono le proiettività, in particolare le proiettività omologiche. Si chiama proiettività omologica una trasformazione del piano tale che:
| Dato un punto S (centro di proiezione) data una retta u (asse dell'omologia), data una coppia di punti A e A' allineati con S ogni altro punto P si trasforma nel modo seguente: |  |
| si tracciano: la retta AP e la si interseca con l'asse; la retta A'Q; la retta SP; si determina così il punto di intersezione tra la retta SP e la retta A'Q; il punto P' è il trasformato di P mediante la proiettività omologica di asse la retta u e centro il punto S. |  |
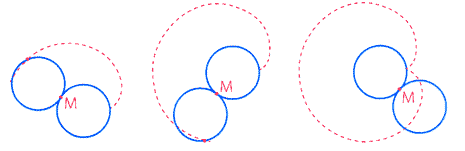
| Il trasformato di una circonferenza può essere una ellisse. |  |
oppure un iperbole o anche una parabola. |  |
| inoltre due segmenti paralleli non si trasformano in segmenti paralleli |  |
L'aggettivo omologico, come è facile verificare, fa riferimento al fatto che tali trasformazioni hanno una retta di punti uniti: i punti dell'asse.
Le coniche tra luce e ombra
Attraverso una torcia elettrica, possiamo vedere un insieme di curve molto importanti per la scienza: le coniche. Per visualizzarle, basta prendere una comune torcia elettrica e proiettare la sua luce su una parete di casa.
| Se l'impugnatura della torcia è rivolta verso la parete, si ottiene approssimativamente una ellisse. |  |
| Se l'impugnatura della torcia è rivolta verso l'esterno, si ottiene approssimativamente una iperbole. |  |
| Se l'impugnatura della torcia è parallela alla parete, si ottiene approssimativamente una parabola. |  |
La cardioide nel piatto e nella tazza
Passiamo infine ad un'altra bella curva che tutti possono vedere formarsi all'interno di recipienti conici e cilindrici illuminati dall'alto. Muovendo il contenitore appaiono varie curve generate dalla riflessione della luce, alcune intrecciate ed altre non intrecciate.
Tra questa la più bella è la cardioide.

La cardioide è una curva ben nota agli studiosi di Ge ometria. Può essere generata in vari modi, ad esempio facendo rotolare una circonferenza attorno ad una circonferenza con lo stesso raggio.
La sua equazione cartesiana, posizionando opportunamente gli assi, è la seguente:
(y2+x2)2-4ax(x2+y2)-4a2y2=0.
Tutti possono riprodurre la cardioide con un software di Geometria dinamica oppure anche con un disegno operando nel modo seguente:
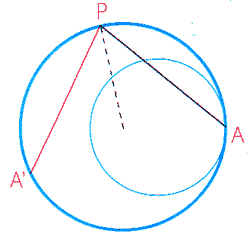
Il cerchio interno ha un raggio che è i due terzi di quello maggiore.
Il punto A è fisso, il segmento arancione è il riflesso del segmento AP.
| Facendo scorrere ol punto P lungo la circonferenza e tracciando un certo numero di segmenti A'P', si ottiene questa immagine | L'inviluppo dei segmenti mostra chiaramente una cardioide. |

Ed ora, tutti a gustare un cappuccino con cardioide!

Per finire, vi invito a seguire la più grande"ombra"visibile dagli uomini, uno dei più straordinari fenomeni astronomici: l'eclisse di sole (una simulazione della prossima eclisse di sole la potete trovare nel sito: http://it.wikipedia.org/wiki/Eclissi_solare).
