NATURA FRATTALE
I FRATTALI NELLA NATURA, LA NATURA DEI FRATTALI
Cos'è un frattale? operando una ricerca su Google, digitando frattali, si ottengono oltre 197 mila voci. Consultando Wikipedia, si legge che un frattale è un oggetto geometrico che si ripete nella struttura allo stesso modo su scale diverse, ovvero non cambia aspetto anche se visto con una lente di ingrandimento. Oggetti con un tale comportamento potrebbero apparire costruzioni artificiali, sebbene siano frequenti in natura: la disposizione dei rami di un albero, la conformazione di un cavolfiore, la distribuzione degli alveoli polmonari, la superficie delle nuvole, il percorso di un fiume, la struttura delle galassie, il lampo di un fulmine, le ramificazioni del deposito di uno ione in un processo elettrolitico, eccetera.
In effetti i frattali sono un nuovo potente linguaggio matematico, grazie al quale è possibile descrivere fenomeni naturali e risolvere problemi della realtà che erano stati un tempo accantonati. Si tratta di una Matematica moderna che si avvale in modo determinante dell'Informatica, anche se la sua genesi è antica.
Per capire l'importanza delle figure frattali, occorre fare un passo indietro nel tempo. Galileo Galilei, uno dei più grandi scienziati di tutti i tempi, riteneva1 che la Matematica fosse una disciplina indispensabile per interpretare i fenomeni na turali e per rappresentare le forme della natura. La nostra esperienza quotidiana ci induce tuttavia a ritenere che le figure geometriche più familiari nello studio (rette, cerchi, poligoni regolari, ...) in natura sono l'eccezione. Qual è la forma di sasso, una nuvola, un albero, una montagna?
È proprio questa l'obiezione di [BENOIT MANDELBROT] che nel 1975 introduce i frattali2 come nuove figure geometriche più efficienti a rappresentare la complessità della natura. Il termine frattale , da lui coniato, deriva dal latino fractus (rotto, frazionato). I frattali sono infatti figure strane, molto frastagliate, granulose, a volte ramificate ed intricate, con tentacoli o protuberanze, proprio come le forme naturali!
A dire il vero, i frattali hanno una radice più antica, che non è solo legata al loro nome. Agli inizi del XX secolo, alcuni matematici avevano creato (ideato e/o inventato) curve e figure molto strane che sovvertivano le regole della Geometria classica violavano le caratteristiche di armonia considerate naturali per gli oggetti in campo scientifico. Una linea tutta spigoli (il merletto di Koch), una curva che dipanandosi un labirinto ricopre un quadrato (curve di Peano-Hilbert , figure bucherellate (polvere di Canton gerla e tappeto di Sierpinski). Queste strutture furono considerate alla stregua di mostri da relegare in una sorta di museo degli orrori o da esibire solo in un circo equestre.
Contemporaneamente, nel mondo scientifico cresceva l'esigenza di trovare un nuovo linguaggio, più duttile e potente, che fosse adeguato a descrivere la complessità della natura. Come afferma Edgar Allan Per "ciò che è nascosto po' essere trovato, purché vengo cercato con sufficiente attenzione e diligenza, mentre ci vuole un intelletto superiore per trovare ciò che si ha sotto gli occhi' Cosi, solo grazie a Mandelbrot i mostri matematici, relegati negli armadi, furono spolverati e rimessi moto acquistando la nuova veste di antenati delle moderne figure frattali. Per dirla con le sue parole, i frattali sono nati recuperando pezzi separati pre-esistenti, ma concepititi in contesti limitati e distinti. Dopo il rivoluzionario intervento di Mandebrot, i matematici furono sorpresi e compiaciuti nello scoprire che le loro figure patologiche fossero diventate la chiave di lettura della complessità tanto a lungo cercata. Negli ultimi venti anni, i modelli frattali sono usciti allo scoperto, acquistando il ruolo dl struttura chiave nella modellizzazione matematica in tutti i settori: dalle scienze naturali a quelle economi che e sociali, dalla fisiologia alla tecnologia avanzata e il loro campo di applicazione è in costante crescita. La geometra franale è inoltre strettamente collegata alla teoria del caos.


Grazie all'accattivante rappresentazione grafica che si può ottenere con l'ausilio di un PC, i frattali hanno acquisito anche uno spazio nel mondo dell'arte: sono nate la pittura e la musica frattale. Quello che invece molti ancora ignorano è che queste figure apparentemente molto complesse e articolate nascondono un segreto di estrema semplicità! Ed è questa forse l'aspetto più sorprendente di tutta la teoria frattale.
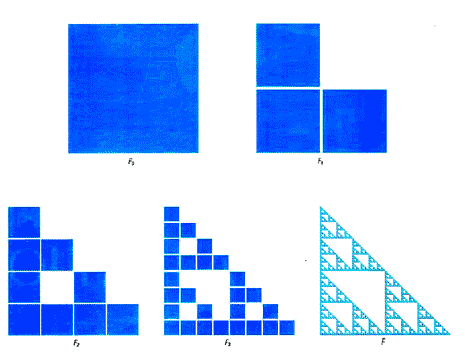
UN ESEMPIO DI FRATTALE — LA GERLA DI SIERPINSKI
Per illustrare come si costruisce una figura frattale, partiamo da un esempio: la gerla di [SIERPINSKI]. Trasformiamo un quadrato F o nella figura F, composta da tre copie ridotte al 50% del quadrato F e .
L'operazione può essere eseguita con una fotocopiatrice: si effettuano tre copie della figura F o ridotte al 50%, successivamente si ritagliano tre quadrati e si incol lano facendo combaciare coppie di lati fino ad ottenere la figura F,. Ripetendo esattamente la stessa operazione a partire dalla figura F,, si ottiene la figura F F e successivamente la figura F 3 .
Procedendo iterativamente, si ottiene (dopo infiniti passi) una figura asintotica E nota come frattale o gerla di Sierpinski. La gerla si ottiene allora mediante un processo iterativo, che consiste nell'applicare ripetutamente, ad ogni passo, la me desima trasformazione: ridurre il quadrato base della metà e triplicarlo! La chiave della figura asintotica risiede pertanto nella trasformazione. Questa agisce come un codice genetico: partendo da un qualsiasi punto, che immaginiamo come cellula madre, si generano per mitosi tre cellule figlia; ciascuna di loro, a sua volta, processo, le varie generazioni cellulari tendono ad una configurazione asintotica di equilibrio, costituita dalla gerla di Sierpinski.
Il nuovo linguaggio proposto da Mandelbrot introduce, attraverso processi iterativi, una " dinamica " nel modello descrittivo della Geometria euclidea. Così, mentre gli elementi del linguaggio tradizionale si visualizzano con facilità, i processi frattali richiedono l'ausilio di un computer. La gerla presenta una curiosa proprietà di invarianza per cambiamento di scala: ingrandendo una porzione della figura, si riottiene la figura stessa. Tale proprietà è detta autosimiglianza ed è caratteristica delle figure frattali.
IL MERLETTO A TRINA DI KOCH
Un altro importante franale classico è il merletto introdotto da Helge [VON KOCH] nel 1904.1n questo caso, il processo è generato dalla trasformazione che muta il segmento F0 nella spezzata F1. Procedendo iterativamente, si ottiene una successione di figure iterate.
Come evidenziato dalle curve iterate, la trina di Koch è una curva tutta punte che mostra una evidente proprietà di autosimiglianza. II merletto di Koch può essere costruito con il metodo del codice genetico a partire da quattro trasformazioni, attraverso un codice di soli 24 parametri.
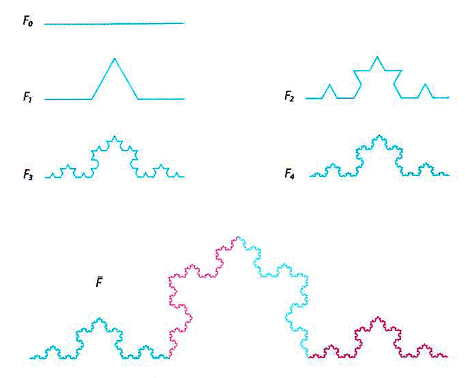
Curva di Koch, generata in Turbo Pascal mediante codice genetico da Benedetta Palladino e Giorgia Quintaliani, classe IV (a.s. 2000-2001), Liceo Scientifico Galilei, Perugia.
È sorprendente che Sierpinskl e Koch abbiano potuto immaginare queste figure senza poterle vedere se non con gli occhi della mente! Non avevano infatti a oro disposizione né fotocopiatrici né PC L'astrazione matematica consente di vedere oltre il possibile e l'ovvio, come la forza creatrice ha consentito a Beethoven dl comporre la IX sinfonia pur essendo diventato sordo! La teoria frattale è un ottimo esempio d'interazione dinamica fra matematica e realtà.
Benoit Mandelbrot nasce a Varsavia nel 1924. Dopo il diploma, all'Ecole Polytechnique di Parigi, ottiene una borsa di studio per il California Institute of Technology. Negli Usa, consegue un master in Aeronautica. Alla fine della guerra, torna a Parigi dove si laurea in Matematica. Attualmente è docente di Matematica alla Harvard University.
Waclaw Franciszek Sierpinski (Varsavia 1882-1969) si laurea in Matematica nel 1904 a Varsavia. Alla fine della prima guerra mondiale, è nominato professore di Matematica presso l'Università di Leopoli.
Anche durante l'invasione nazista della Polonia, continua la sua opera in un'Università clandestina.
Qualche libro:
- M.Barnesley, Fractals Everywhere, AP Professional (1988)
- P. Brandi, A Salvadori, Modelli Matematici Elementari, Bruno Mondadori (2004)
- H.O. Peitgen, H. Jurgens, D. Saupe, Fractal for the Classroom, I&II, Springer-Verlag (1992)
Helge von Kock (Stoccolma 1870-1924) ha studiato presso l'Università di Stoccolma, dove ha poi conseguito il dottorato in Matematica.
"Il libro della natura è scritto in lingua matematica ed i suoi caratteri sono triangoli, cerchi e figure geometriche, senza i qual mezzi è impossibile a intenderne umanamente parola; senza questi è un aggirarsi vanamente per un'oscuro labirinto". Il Saggiatore
[...] la geometria Euclidea è incapace di descrivere la natura nella sua complessità, in quanto si limita a descrivere tutto cò che è regolare [...] mentre osservando la natura vediamo che le montagne non sono dei coni, le nuvole non sono delle sfere, le coste non sono dei cerchi". Les Object Fractal (1975).

