Quel favoloso XII secolo per la Matematica
La curva dell’accrescimento della Matematica, non limitando l’osservazione a particolari nazioni o continenti, è un grafico di una funzione a = a(t) monotona non decrescente: considerati due tempi t1< t2 si ha in corrispondenza a(t1) ≤ a(t2).
Questo potrebbe implicare alcuni intervalli di tempo in cui la funzione si mantiene costante, ma anche discontinuità di prima specie o “salti” in corrispondenza del presentarsi di particolari matematici creatori. Vi possono essere intervalli di tempo in cui la crescita è modesta ed altri in cui essa è maggiormente rilevante. Uno di questi ultimi si può notare nel secolo XII. Trascurando i molti matematici di contorno che pure determinarono un favorevole tessuto connettivo, troviamo in Persia i grandi risultati del matematico, astronomo e poeta Omar Khayyam (1044 – 1123/24); in India quelli di Bhaskara Acharya (1114 – 1185 ca.) e in Occidente le opere di Leonardo Pisano (1170 – 1228 ca.). Mi troverei in imbarazzo se dovessi scegliere, tra questi grandi matematici, il maggiore. Forse per originalità dovrei scegliere tra i primi due ma per importanza storica sarei propenso a dare maggiore importanza al terzo, almeno per quanto riguarda la diffusione della Matematica in Occidente. Da un punto di vista storico, il XII è il secolo centrale delle Crociate. La conquista di Gerusalemme avvenne nel 1099 alla fine della prima Crociata e la quarta ebbe inizio nel 1202.
Non tutti gli storici concordano sulla circostanza che le Crociate favorirono gli scambi commerciali e culturali. Alcuni sono dell’opinione che esse piuttosto interruppero entrambi. Per quanto riguarda la Matematica, comunque, è proprio dal nostro secolo XII che iniziarono le traduzioni dall’arabo delle grandi opere [1]. Così nel 1142 Adelardo di Bath traduce per la prima volta (dall’arabo) gli Elementi di Euclide precedendo di poco molti altri traduttori tra cui Roberto di Chester che tradusse l’Algebra di Al Kuwarizmi, Platone di Tivoli (vissuto a Barcellona verso il 1134 e il 1145) che tradusse vari testi arabi e greci e il Liber Embadorum di Savasorda e, specialmente, Gherardo da Cremona (1114 – 1187) che tradusse ben 85 opere di Matematica tra cui gli Elementi di Euclide e l’Almagesto di Tolomeo. Notiamo, infine, la nascita di Federico II (1194 – 1250) che tanto contribuì alla diffusione della cultura: egli fondò tra l’altro l’Università di Napoli che oggi porta il suo nome [2] e al cui seguito vi era un certo Giovanni da Palermo, matematico, che con i suoi quesiti costrinse, come vedremo, Leonardo Pisano alla stesura di vari e importanti lavori.
Omar Khayyam (nato a Nisciapur, cittadina della Persia nord orientale) è, a giudizio personale di chi scrive, essenzialmente un poeta: le sue Quartine hanno una consapevolezza della fragilità umana e una sofferta e nascosta religiosità che possono paragonarsi alle grandi liriche di ogni tempo. Ma non è questa la sede per parlare di poesia. Così non parlerò nemmeno del suo valore come astronomo, testimoniato dall’incarico che ebbe dal sultano Jalad eddin Malik shah per la riforma del calendario. Tratteggerò invece brevemente il suo valore matematico, rilevante sia in Geometria che in Algebra. Appare notevole in Omar Khayyam il senso critico e la capacità mostrata in Geometria per vari risultati di buona importanza. La sua originalità appare maggiormente per la via seguita nel cercare di dimostrare il V postulato di Euclide aprendo una strada seguita poi da Nasir Eddin (1201 – 1274) e successivamente, con incredibile somiglianza, da Gerolamo Saccheri (1667 – 1733), cosa tanto più incredibile in quanto questi ignorava assolutamente i risultati del matematico persiano. Omar Khayyam conosceva il commento di Simplicio relativo ad una dimostrazione del V postulato, Erone “il meccanico” ed Euclide. Conosceva altresì i tentativi di dimostrazione del V postulato fatti da cinque studiosi arabi ma, nonostante questo, la sua trattazione è, come detto, originale.
La sua capacità in Geometria appare anche nella abilità di adattare il metodo mostrato da Archimede nella risoluzione del cosiddetto “problema complementare”e per la costruzione delle radici di qualsiasi equazione di terzo grado. Risultato di importanza geometrica, ma di assoluto valore anche per l’Algebra. Riguardo al primo argomento che intendiamo mettere in luce, Omar Khayyam prende spunto dal “quadrilatero birettangolo isoscele” ABCD che diverrà famoso in seguito con Saccheri (l'angolo A è uguale all'angolo B = 1R; AC = BD) [3]. Come farà in seguito Saccheri, Omar Khayyam dimostra che in questo caso (1a prop.) gli angoli ACD e BDC sono uguali [4]. Nella seconda proposizione, mandando dal punto medio del lato AB la perpendicolare al lato stesso, Omar Khayyam dimostra che essa incontra perpendicolarmente il lato CD opposto nel punto medio [5]. Si distinguono a questo punto le tre ipotesi a seconda se si considerano acuti, ottusi o retti gli angoli uguali ACD e BDC. Ma, mentre Saccheri comincia a sviluppare le tre ipotesi alla ricerca dell’assurdo proveniente dalle prime due, Omar Khayyam con la supposizione che rette parallele sono equidistanti (considerazione equivalente al V postulato!) dimostra l’ipotesi dell’angolo retto da cui, tautologicamente quindi, è possibile dimostrare il postulato. Di grande importanza è poi la costruzione geometrica della radice di una qualsiasi equazione di terzo grado mediante l’uso delle coniche, che egli mostra di conoscere perfettamente. D’altra parte, è lui stesso a scrivere che senza la conoscenza di Euclide e di Apollonio non è possibile seguire le sue costruzioni. Egli classifica le equazioni di secondo e terzo grado dimostrando un senso algebrico notevole [6]. Omar Khayyam non riesce, però, a scrivere una formula radicorazionale per il calcolo delle radici delle equazioni. Ne è pienamente consapevole e scrive infatti che “forse altri dopo di noi saranno capaci di riempire il vuoto” [7]. La sola costruzione delle radici, e quindi della loro esistenza, avrebbe però spinto maggiormente i matematici alla ricerca anche delle formule corrispondenti e Cardano non avrebbe potuto più dire che non si era applicato alla loro risoluzione poiché Luca Pacioli ne aveva scoraggiato lo studio [8]. Ma la sua opera, anche se conosciuta in tutto l’Oriente, entrò in Occidente solo a partire dal XIX secolo, quando ormai l’argomento delle equazioni di terzo (e quarto) grado era stato affrontato e pienamente risolto. Come unico esempio vediamo la costruzione di un segmento che verifichi l’equazione generale (un cubo e lati uguale a numero) x3+ ax = b a cui si può ricondurre, come sappiamo oggi, qualsiasi altra equazione di terzo grado. Omar Khayyam segue un criterio di omogeneità per poter confrontare i vari termini dell’equazione rappresentati da figure geometriche. In questo senso, considerando l’incognita una linea, considera il coefficiente a dell’incognita uguale ad una certa superficie AB2 e il termine noto b al volume AB2•BC. Teniamo inoltre presente che dopo il testo di Apollonio sulle coniche, noto ad Omar Khayyam, i matematici greci consideravano “data” una parabola, cioè disegnabile anche se non con riga e compasso, allorché se ne fossero conosciuti l’asse, il vertice e il parametro. Ricordiamo anche che, preso un punto M della curva e condotto per esso il segmento MN di perpendicolare all’asse, il quadrato costruito su tale segmento è equivalente al rettangolo che ha per dimensioni la parte di asse che si è determinata e il parametro stabilito. In altre parole, disegnata la parabola con asse VN, vertice V e parametro p, si ha MN2 = VN•p. Omar Khayyam, con a = AB2 e b = AB2•BC, considera la parabola avente la retta AB come asse, vertice B e parametro AB. Inoltre BC viene posto tangente alla parabola in B. Egli considera poi la semicirconferenza di diametro BC, indicando con D il suo punto comune alla parabola. Dal punto D, noto, si ottengono i punti Z e E mandando rispettivamente le perpendicolari all’asse e al diametro considerati. Da quanto detto, si ha:
DZ2 = BZ•AB cioè BE2 = ED•AB e dunque AB:BE=BE:ED.
Per una proprietà della circonferenza, si ha inoltre:
BE : ED = ED : EC.
Pertanto:
AB : BE = BE : ED = ED : EC da cui AB2:BE2=BE:EC[9]
e dunque l’uguaglianza tra i solidi AB2•EC = BE3.
Con EC = BC – BE, sommando ai due membri il volume AB2•BE e semplificando, si ha l’uguaglianza:
AB2•BC = BE3 + AB2•BE cioè b = BE3 + a•BE
e questo mostra che BE è soluzione dell’equazione data x3+ ax = b.
Il messaggio di Omar Khayyam venne raccolto da Sharf alTusi (morto nel 1213 ca.) che proseguì l’indagine algebrica perfezionando il metodo delle sostituzioni di variabili e avvicinandosi, anche se con metodo geometrico, a condizioni di risolubilità che si ritroveranno in seguito nella famosa formula risolutiva delle equazioni di terzo grado [10].
Dalla Persia facciamo un passo verso est e portiamoci in India dove, nel XII secolo, troviamo il grande matematico Bhaskara Acharya (“il maestro”) nato a Bijjada Bida (oggi distretto di Bijapur). Bhaskara non è un poeta come Omar Khayyam anche se talvolta esprime i suoi quesiti in forma poetica [11] e, come molti matematici indiani, scrive le sue regole matematiche in versi. Numerosi sono i risultati ottenuti da Bhaskara in Aritmetica e in Algebra ed anche in quella disciplina che sta a cavallo di queste due: l’Analisi indeterminata. Bhaskara fu un valido astronomo, favorito anche da suoi studi sulla sfera, e anche un apprezzato astrologo. L’Algebra indiana, pur tenendo conto delle varie influenze che ricevette dalle Matematiche di altre civiltà, mostrò una sua indipendenza, ad esempio affrontando l’Algebra senza il concorso della Geometria come solo Diofanto di Alessandria (3° sec. d. C.) aveva mostrato. In tal modo si opera sull’incognita come fosse un comune numero, senza ricorrere a pesanti rappresentazioni geometriche e senza problemi di omogeneità dei vari termini. Le operazioni per ottenere i valori dell’incognita sono, pertanto, assolutamente aritmetiche; i numeri negativi possono entrare a pieno titolo così come il fondamentale “zero”. Con Bhaskara il procedimento algebrico raggiunge una piena efficienza. D’altra parte, il titolo della sua opera algebrica Virja-Ganita vuol dire “scienza di calcolo con le incognite”. In essa viene anche indicato il metodo generale per raggiungere la formula risolutiva di un’equazione di secondo grado [ax2+bx=c] alla stessa maniera del nostro usuale procedimento. Ecco infatti la regola di Bhaskara: “Moltiplica entrambi i membri di un’equazione per un numero uguale a quattro volte il [coefficiente del] quadrato [4a] e aggiungi a questo un numero uguale al quadrato [4b] del numero originale [cioè del coefficiente che si aveva prima della moltiplicazione indicata] dell’incognita”. Il seguito è chiaro: si tratta proprio della costruzione della formula risolutiva così come ancora oggi facciamo [12]. Per equazioni di grado superiore al secondo, Bhaskara, trattando casi particolari, è in grado di abbassarne il grado. Osserviamo, ad esempio, l’equazione x4–2x2 – 400x = 9999 che prima scrive nella forma x4–2x2 + 1 = 400x + 10000; poi, osservando che il secondo membro non è, come lo è il primo, un quadrato perfetto, aggiunge ai due membri 4x2 in modo da ottenere (x2 + 1)2 = (2x + 100)2. Come si vede, questi procedimenti – pur limitati a casi numerici – sembrano preludere al metodo di risoluzione delle equazioni di quarto grado seguito da Ludovico Ferrari [13].
Abbandoniamo l’Algebra di Bhaskara, che pure mostra come affrontare anche casi di equazioni irrazionali, e accenniamo ad uno dei risultati più importanti del nostro matematico indiano. Si tratta di quell’Analisi indeterminata che si presenta allorché si cercano solo radici intere, in equazioni in cui sono presenti più di una incognita. Questa ricerca, attraverso varie espressioni, si trasformerà nel corso dei secoli sino a prendere da una parte la strada più decisa della Teoria dei numeri e, dall’altra, quella della Geometria analitica.
Le origini sono antiche. Si presentano, ad esempio, con il cosiddetto fiore di Timarida (V-IV secolo) [14] e con il famoso problema dei buoi di Archimede [15]. In India, Aryabhata (V sec. d. C.) risolve l’equazione indeterminata ax + by = c con un metodo simile a quello usato da Euclide per la determinazione del massimo comune divisore di due numeri (algoritmo euclideo) ed a quello considerato anche da Lagrange. Sulla soluzione di tale equazione ritornano anche Brahmagupta (VI secolo) e Bhaskara. Nella Matematica indiana viene affrontata da Brahmagupta anche la cosiddetta equazione di Pell¬Eulero x2– Ay2=1 (con A non quadrato perfetto) che verrà, come vedremo, ripresa anche da Bhaskara. È difficile stabilire se i risultati ottenuti da Brahmagupta risultarono, come a noi oggi appaiono, premesse per quelli di Bhaskara. Ad ogni modo osserviamo che, supposti x = p, y = q,e x = p’, y = q’ soluzioni (intere) rispettivamente delle equazioni x2– Ay2= s e x2– Ay2= s’ indicate schematicamente con (p, q; s)e(p’, q’; s’), allora x = pp’± Aqq’ y = pq’± p’q è soluzione dell’equazione [16] x2– Ay2= ss’ [17].
Questo risultato consente a Brahmagupta di ottenere varie soluzioni nel caso particolare di s = s’ e successivamente, se fosse s = s’ = ± 1 (ma anche quando s = s’=± 2 [18]), di risolvere l’equazione di Pell-Eulero, sempre però supponendo che vi siano soluzioni per tali valori di s. Con successive applicazioni delle “regole di produzione”, è possibile ottenere infinite altre soluzioni (p, q; s) dell’ equazione variando opportunamente s. Si noti che, naturalmente, fissati un valore per la x, per la y e per A, si ottiene un determinato valore di s avendo così una vera soluzione dell’equazione e quindi infinite altre. La difficoltà consiste nell’ottenere soluzioni allorché si fissi preventivamente il valore di s e, per l’equazione di Pell-Eulero, con s = ± 1 oppure s = ± 2. Se però fosse nota una soluzione effettiva dell’equazione di Pell-Eulero, allora se ne potrebbero ottenere (sempre con le regole di produzione) infinite altre [19] ma non si sarebbe comunque risolta l’equazione in generale. “Con ciò si era ancora ben lontani dalla soluzione generale” osserva Andrè Weil [20] ed è qui che entra in campo Bhaskara Acharya [21].
Scelti due numeri p e q primi tra loro, si può determinare un valore di r in modo che il numero:
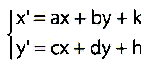
sia intero [22] e scelto in modo che la differenza r2 – A risulti la più piccola possibile. In tal caso, il numero:
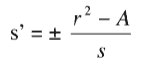
risulta essere intero e:
è una soluzione dell’equazione x2–Ay2= s [23]. Procedendo per questa via, a partire dai valori ottenuti p’, q’, s’, si ottengono via via nuove soluzioni applicando quel cosiddetto “metodo ciclico” simile al metodo della discesa di solito attribuito a Fermat [24] che porta ad una soluzione, generale quindi, dell’equazione di Pell-Eulero se si giunge ad un valore di s uguale a ± 1 oppure ± 2. La dimostrazione di Bhaskara sarebbe accettabile solo presupponendo l’esistenza di una soluzione intera, con la sicurezza che in questa discesa si possa arrivare, ad esempio, al valore di s =1. Bisognerà aspettare Lagrange per avere la dimostrazione della risolublità completa dell’equazione di Pell-Eulero [25]. Questo risultato si ottiene sempre, dato che l’equazione di Pell-Eulero è effettivamente risolubile, ma Bhaskara non sentì l’esigenza di una dimostrazione, forse impegnato in soli casi particolari. L’esigenza fu per prima sentita da Fermat ma sviluppata completamente da Lagrange [26]. Questo toglie poco al grande risultato mostrato da Bhaskara. Suo merito è aver aperto la strada alla dimostrazione generale dell’equazione tanto che Hermann Hankel, al termine della sua analisi, afferma che il metodo indiano “è superiore ad ogni lode; ed è certamente il più acuto argomento che fu raggiunto nella Teoria dei numeri prima di Lagrange”. L’equazione di Pell-Eulero ha avuto una grande importanza per lo sviluppo della Matematica. Nata in alcuni casi particolari per il calcolo approssimato di radici quadrate di numeri interi [27], è stata poi applicata a vari altri problemi (si ricordi il problema dei buoi di Archimede) e affrontata con diversi metodi (Teoria dei numeri; frazioni continue, congruenze…).
Nello stesso secolo XII troviamo – in Occidente questa volta– altri matematici, tra i quali primeggia Leonardo Pisano.
Cercheremmo invano, nelle sue opere, la vera poesia di Omar Khayyam o le espressioni poetiche di Bhaskara. La sua Matematica è solo Matematica che però, a giudizio di chi scrive, è essa stessa poesia. L’importanza fondamentale di Leonardo Pisano sta nel fatto che egli riportò con le sue opere non solo la Matematica greca, araba e indiana, cioè tutta la Matematica nota in quel tempo (fatta eccezione, come sappiamo, per quella di Omar Khayyam che non conobbe), ma la espose con le relative dimostrazioni (certa probatione) in modo da farla capire, gustare e nel caso accrescere. Questo suo proposito viene espresso esplicitamente già nella prima pagina del suo Liber Abaci “affinché la gente latina, sino a qui ignara, si istruisca”. Egli espose pertanto in maniera sistematica l’Aritmetica e l’Algebra sino ad allora note, dimostrando le regole esposte in quest’ultima mediante proposizioni tratte dagli Elementi di Euclide e sfruttando qualche risultato cui era giunto il matematico ebreo Savasorda (Joannes Hispalensis, nato a Toledo tra il 1089 e il 1092 e morto a Roma nel 1167 circa), autore del Liber Embadorum. La dimostrazione consente di capire il perché di un certo risultato, di criticarlo se è il caso e di ampliarlo se se ne ha la capacità. In altre parole, la dimostrazione è il preludio ad un ulteriore sviluppo. A Leonardo Pisano risalgono, tra l’altro, l’introduzione della scrittura posizionale, le cifre per la scrittura dei numeri (secondo il metodo degli Indi, come egli ricorda) e l’uso dei numeri negativi, anche questi appresi nei suoi viaggi di istruzione [28]. Leonardo Pisano non si limitò a questa trasmissione, che rappresenta forse il suo contributo maggiore, ma fu egli stesso un matematico creatore, sia in problemi di Geometria (uso ad esempio del segmento unitario [29], lontano parente di quello che poi useranno Bombelli e massimamente Descartes), sia nelle risoluzioni che si trovano nel Flos e nel Liber quadratorum. Nel Flos, Leonardo Pisano affronta l’equazione x3+2x2+ 10x = 20 che gli era stata proposta da Giovanni da Palermo, matematico – come già detto – alla corte di Federico II [30]. Egli “costruisce” geometricamente il primo membro dell’equazione, secondo il metodo usato per le equazioni di secondo grado, e dimostra che nessuna delle quindici linee razionali e irrazionali del X libro degli Elementi di Euclide può risolvere l’equazione [31]. Dopo la dimostrazione di questa impossibilità, Leonardo Pisano dà comunque una radice dell’equazione nella forma: 1 22I 7II 42III 30IV 4V 40VI cioè 1 + 22/60 + 7/602 + 42/603 + 30/604 + 4/605 + 40/606 = 1,36880810785 valore esatto sino alla decima cifra decimale [32]! Una particolarità significativa del procedimento sta anche nel fatto che Leonardo Pisano, per rappresentare con la Geometria piana il primo membro dell’equazione, non esita ad indicare con x3 la superficie di un rettangolo mostrando una sostanziale indipendenza dalla Geometria stessa. Non era questa una vera novità poiché anche in una tavoletta babilonese [33] si operava al di fuori di una rappresentazione geometrica ed Erone, in un suo esercizio, aveva sommato una “linea” con un’“area” [34].
Nel Liber quadratorum, Leonardo Pisano risolve un altro problema propostogli sempre da Giovanni Panormita: “trovare un numero quadrato che aumentato o diminuito di cinque determini un numero quadrato”. La risposta di Leonardo Pisano, ottenuta mettendo in luce molte proprietà sui numeri quadrati [35], tra cui anche sei modi diversi di risolvere l’equazione pitagorica (in casi particolari ma anche, l’ultimo, in forma generale), fu quella del numero razionale (3+5/12)2. Infatti: (3+5/12)2 – 5 = (2+7/12)2; (3+5/12)2 + 5 = (4+1/12)2. Non si deve pensare, però, che il Liber Abaci e la Pratica Geometriae siano semplici rassegne di risultati già noti, solo un’enciclopedia ragionata preziosa per lo sviluppo successivo della Matematica. In tali opere si trovano anche interessanti spunti e ricerche: si pensi, ad esempio, al notissimo problema dei conigli [36] e ai suoi sorprendenti sviluppi e legami con i coefficienti binomiali, le frazioni continue, la sezione aurea e persino il problema di Hilberto. Ricordiamo poi il problema (Importante problema relativo a quattro uomini e una borsa da essi ritrovata [37]) nel quale si ottiene la soluzione solo stimando negativi i soldi posseduti da uno degli uomini, mostrando appunto l’uso dei numeri negativi che, oltre tre secoli dopo, Cardano chiamava ancora ficti, falsi [38], facendoli così conoscere [39]. O ancora un singolare problema (Notevole quesito su un lavoratore [40]) in cui Leonardo Pisano risolve un “problema di miscuglio” non mischiando, ad esempio, due tipi diversi di riso o di vino, ma i giorni di un mese con i soldi presi per il mese totalmente lavorativo [41]! Si potrebbe seguitare ancora e, anche passando alla Pratica Geometriae, mostrare ad esempio il capovolgimento della consuetudine matematica secondo la quale era la Geometria a dimostrare proprietà algebriche e aritmetiche mentre qui sono queste talvolta a soccorrerla, mutamento di non poco conto. Così è in tale opera che egli migliora l’approssimazione archimedea di pigreco [42]. È possibile però, a mio parere, già con questi cenni, valutare l’importanza che ebbe l’opera di Leonardo Pisano nella Matematica occidentale.
Prima di terminare questo lavoro, osserviamo che nel nostro secolo XII anche in tutt’altra parte, in Cina, si respira aria di rinnovamento generale e matematico in particolare. Non entro nel merito delle origini della Matematica cinese e dei suoi scambi con quella babilonese e indiana, sui quali per altro non si è ancora raggiunta una pienezza di consensi. Osservo però che dal 960 al 1280 vi è in Cina “il periodo Sung [che] produsse – scrive Joseph Needham [43] – alcuni tra i più grandi matematici cinesi di ogni tempo, in particolare Chin Chiu-Shao, Li Yeh e Yang Hui. Il periodo Sung, forse sotto lo stimolo dell’influenza araba (…), fu l’epoca dei grandi algebristi, e la Cina fu il Paese in cui questo ramo della Matematica raggiunse in tali secoli i massimi risultati” [44].
Abbiamo visto che, in varie parti del mondo, il secolo XII segna un intervallo di tempo in cui – per parlare della sola Matematica – si ha un notevole rinnovamento. Da ogni parte si ha un ritorno consapevole della dimostrazione, senza la quale la Matematica diventa un ricettario di formule vere o solo approssimate, adatte ad un esclusivo uso prati-co. La dimostrazione consente di capire quello che si studia, ne consente una critica e la possibilità di ulteriori sviluppi. Si assiste, nel secolo preso in esame, al ritorno delle grandi opere antiche che permisero anche il ritorno di tanti risultati raggiunti ed appunto anche la loro dimostrazione. Abbiamo indicato alcune grandi personalità che contribuirono al successivo sviluppo della Matematica nei suoi vari aspetti, preparando un rifiorire di tale scienza che non tardò a presentarsi. A tutto ciò si aggiunse, sempre nel nostro “favoloso secolo”, e non è avvenimento di poco conto, la nascita a Bologna della prima Università occidentale (1158) [45], seguita ben presto da altre in vari Paesi, con un rinnovamento diffuso anche in altre discipline e una crescita non più episodica degli studi che porterà ben presto al cosiddetto “Rinascimento”. Singolare, dunque, ed eccezionale questo secolo XII: i suoi matematici stavano creando una scienza nuova e forse non se ne rendevano pienamente conto!
CONCLUSIONE
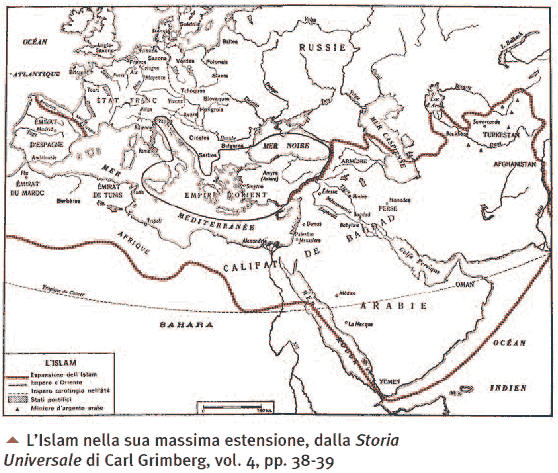
A questo punto vorrei tentare una spiegazione della straordinaria fioritura matematica avvenuta nel secolo in esame. Si tratta ben inteso di una ipotesi anche se, a mio parere, verosimile. Dopo appena un secolo esatto dalla morte di Maometto (632), vi fu la battaglia di Poitier nella quale i Franchi dovettero contrastare in Francia la straordinaria espansione araba [46]. Ebbene, la grande forza dell’Islam conquistò in pochi secoli parte dell’Europa, dell’Africa del nord e il medio Oriente, come mostrato nella cartina di pag. 47. I barbari invasori ben presto assorbirono le culture dei Paesi conquistati e di quelli confinanti rovesciando, come è stato osservato da Gioacchino Volpe, il famoso detto Graecia capta ferum victorem cepit che però aggiunge subito dopo [47]: “Sì, certo, ancora “ferum”, nell’XI e XII secolo; ma di una barbarie che, sotto la sottile crosta, celava tesori di energia creativa ed originalità potente che dal di fuori attendeva solo aiuti e suggestioni: nell’arte come nelle altre attività spirituali”. Bisogna dire che, nella Matematica, quella originalità detta non si manifestò in maniera molto significativa. Il merito degli studiosi arabi (molti erano persiani “capti”, per dir così) fu quello assai importante di aver tradotto, studiato e compreso le grandi opere greche e tratto profitto dai risultati indiani, persiani e giudei unificando questo sapere grazie all’uso della lingua araba che veniva usata in tutto il territorio conquistato. In questo modo, l’unificazione politica e l’eliminazione di pastoie dovute a confini e all’uso di lingue diverse trasmisero in tutto il vasto territorio islamico una cultura di base elevata sulla quale poterono svilupparsi quei grandi matematici che abbiamo visto [48]. Mi sembra dunque – è questa, ripeto, una ipotesi piuttosto verosimile – che una delle principali cause che resero il XII secolo così “favoloso” per lo sviluppo della Matematica sia stata l’espansione culturale a seguito di quella geografica e politica della civiltà araba. Quando il risveglio politico dell’Europa si rivolse anche alle scienze, oltre che ai tesori conservati nelle biblioteche monastiche e successivamente alle opere che vennero insieme agli studiosi che scapparono da Costantinopoli in seguito all’invasione turca (1453), per apprendere almeno inizialmente molti risultati della Matematica greca, i suoi studiosi dovettero apprendere l’arabo prima del greco per poter leggere i grandi risultati della Matematica antica. Scrive a questo proposito Carl Boyer [49]: “All’inizio del XII secolo nessun europeo avrebbe potuto pretendere di essere un matematico o un astronomo vero e proprio senza una buona conoscenza dell’arabo (…) ma alla fine del secolo proprio dall’Italia cristiana doveva provenire il più eminente e originale matematico del mondo di allora [Leonardo Pisano]. Fu questa in maniera così eminente, un’epoca di transizione da un vecchio ad un nuovo modo di vedere, tanto che C. H. Haskins intitolò la sua opera “Il Rinascimento del XII secolo”. La rinascita di cui parla cominciò necessariamente con un dilagare di traduzioni”. Il Rinascimento era dunque alle porte, ma in Matematica era già iniziato.
BIBLIOGRAFIABHASKARA A., (a) “Lilavati” in Algebra with Arithmetic and Mesuration from the Sanscrit of Brahemegupta and Bhaskara, trad. di H. T. Colebrooke, London, Myrray, 1817, pp. 1-127; (b) “Vija-Ganita”, ivi, pp. 129-276. BOYER C. B., A History of Mathematics, New York, London, Sydney, Wiley, 1968 (Storia della matematica, trad. di A. Carugo, Milano, ISEDI, 1976). DJEBBAR A., “Una panoramica della matematica” in La matematica. I luoghi e i tempi, Einaudi, Torino, 2007, pp. 177-208. FRAJESE A., Attraverso la storia della matematica, Le Monnier, Firenze, 1969. GABRIELI F., Maometto e le grandi conquiste arabe, Il Giornale, Biblioteca storica, Mondadori, vol. 29. GRIMBERG C., Storia universale, Dall’Oglio, Milano, vol. IV, 1965. GUJAR L. V., Ancient indian mathematics and Vedha, Bombay, Printed at the Aryabhushan Press, 1947. HEATH T., Diophantus of Alexandria. A study in the history of greek Algebra, Cambridge, University Press, 1910. KONEN H., Geschichte der Gleichung t2 – Du2 = 1, Hirzel, Leipzig, 1901. LAGRANGE G. L., Oeuvres de Lagrange, Paris, Gauthier-Villars,T. VIII, 1879. LEONARDO PISANO (Fibonacci), Tre scritti inediti di Leonardo Pisano pubblicati da Baldassarre Boncompagni, Firenze Tip. Galileiana, 1854; MARACCHIA S., Storia dell’Algebra, Liguori, Napoli, 20082. NEEDHAM J., Science and civilisation in China, with the collaboration of Wang Ling, Cambridge, University Press, Vol. III, 1959 (Scienze e Civiltà in Cina, III, trad. M. Baccianini e G. Mainardi, Einaudi, Torino, 1981). OMAR K., Al-Khayyam mathématicien (par R. Rashed et B. Vahabzadeh), Blanchard, Paris, 1999. SACCHERI G., Euclide liberato da ogni macchia, Bompiani, Milano, 2001. VOLPE G., Il Medio Evo, Sansoni, Firenze, 1958. WEIL A., Teoria dei numeri. Storia e matematica da Hammurabi a Legendre, Einaudi, Torino, 1993. |
NOTE[1] Scrive C. Boyer ([1976] p. 293): “Ad ogni modo i canali che pas-savano per la Spagna e per la Sicilia erano più importanti nel XII secolo e vennero lasciati in gran parte intatti dalle armate saccheggiatrici e distruttrici dei crociati nel periodo che va dal 1096 al 1272. La rinascita del sapere nell’Europa latina ebbe luogo durante le Crociate ma probabilmente si verificò nonostante le Crociate”. Boyer non parla solo della Matematica ma della cultura in generale. In questo senso, causato o no dalle crociate, vi è nel XII secolo un grande movimento europeo ed un risveglio commerciale indipendente, prima e dopo. Questo bene emerge dalle dense analisi di Gioacchino Volpe (Il Medio Evo [1958], cap.XV – Crociate, Moto migratorio italiano, colonizzazione tedesca – e specificatamente il parag. V-Riattivate correnti di cultura) che, tra l’altro, considera assai importante la nascita dei linguaggi volgari in Francia, Germania e Italia e la nascita “del desiderio della cultura disinteressata” (p. 239-240). [2] L’Università venne chiamata Studium e fu forse la prima Università completamente statale. [3] Cfr. Omar Khayyam [1999] p. 323. Le lettere A, B, C, D sono state messe da me per facilitare la comprensione delle proposizioni. [4] In Saccheri si segue la stessa dimostrazione ma nelle due prime proposizioni gli angoli in A e in B si considerano soltanto uguali e non retti, come in Omar Khayyam; cfr. Saccheri [2001]. [5] Questa è anche la 2a proposizione di Saccheri che però unisce i due punti medi dei lati AB e CD e dimostra che la retta ottenuta è perpendicolare ai due lati. Le due dimostrazioni sono molto simili. [6] Riguardo alla classificazione operata da Omar Khayyam, R. Rashed e B.Vahabzadeh vedono un parallelo, non una derivazione, con quello che farà in seguito Descartes ma brevemente tratteggiato (O. Khayyam [1999], pp. 15-16) e scrivono nell’introduzione: “Mi fermerò un momento per un confronto tra questo programma annunciato e quello che era stato realizzato da al-Khayyam. Si concluderà immediatamente che il progetto concepito da Descartes, quale egli formula nel 1619, è, nello stesso tempo, al di qua e al di là di quello di al-Khayyam”. [7] Per le costruzioni di Omar Khayyam della radice reale di una qualsiasi equazione di terzo grado (vengono presentati nel dettaglio i tre casi: x3+ax2= bx; x3+ ax = b (che vedremo) e x3+ ax2+ bx = c) rimando alla mia Storia dell’Algebra [2008] (pp. 215-225) per le varie considerazioni inerenti e i rinvii bibliografici. [8] Questo scrive Cardano nelle prime parole della sua Ars Magna del 1545. [9] Dalla catena di rapporti si ha AB/BE = BE/ED e AB/BE = ED/EC; moltiplicando membro a membro si ha il risultato del testo. [10] La disuguaglianza stabilita da Shaf al-Tusi porta ad essere positivo il radicando della radice quadrata presente nella formula risolutiva dell’equazione di terzo grado e, nella consapevolezza che abbiamo oggi, conduce al caso di una sola radice reale. [11] Ecco, ad esempio, un problema posto nella sua opera che aveva chiamato Lilavati forse dal nome di sua figlia (Bhaskara [1817] pp. 24-25): “Un quinto di uno sciame di api si posa su un fiore di Kadamba, un terzo su un fiore di Silindha. Tre volte la differenza tra i due numeri volò sui fiori di un Kutuian, e rimase solo un’ape che si librò qua e là per l’aria, ugual-mente attratta dal profumo di un Gelsomino e di un Pandamus. Dimmi tu ora, donna affascinante, qual era il numero delle api”. Chi assegnerebbe oggi l’equazione: 1/5 x + 1/3 x + 3(1/3 x – 1/5 x)+1= x (con x numero delle api) con questa presentazione poetica? Notiamo che Bhaskara risolve il pro¬blema usando la “falsa posizione” e lo risolve anche usando un’equazione di primo grado [ivi p. 192]. [12] Bhaskara, Virja-Ganita [1817] pp. 209-210. Si noti che sino a Bombelli (ma ancora per qualche tempo dopo) non veniva con-siderato un membro uguale a zero. Si consideri l’esempio di Bhaskara (ivi pp. 217-218): 8x2 – 252x = -162. Per mostrare che anche la regola detta viene applicata con intelligenza, Bhaskara moltiplica in questo caso i due membri solo per 2, dato che in questo modo il coefficiente di x2 risulta ugualmente un quadrato perfetto. Seguendo la regola, ottiene (4x -63)2 = 272 da cui le due radici x = 45/2; x = 9 (si noti che, per il problema da cui è venuta l’equazione, la radice da accettare è solo la prima ma in altre circostanze Bhaskara può considerarle entrambe, positive o negative che siano). [13] Cfr. S. Maracchia [2008] pp. 302 sgg. [14] La data indicata è quella che viene considerata più probabile ma vi sono anche opinioni diverse; per l’intero argomento cfr. S. Maracchia [2008] pp. 21 sgg. [15] Per il problema dei buoi di Archimede cfr. S. Maracchia [2008], pp. 113-116. [16] Regole bhavana (“regole di produzione”). [17] Per verificare questa affermazione, basta eseguire l’opportuna sostituzione. [18] In questo caso risulta ss’ = 4 e quindi x2e y2 sono divisibili per 4 ottenendo un’equazione di Pell-Eulero. [19] Si consideri, con A = 2, la soluzione (3, 2, 1). Combinando questa con se stessa, si ottiene con la regola di produzione, con lo stesso valore di A, la soluzione x = 3•3 ± 2•2•2 ed y = 2•3 ± 3•2 e, con i segni superiori la soluzione (17, 12; 1) ecc. ecc. [20] A. Weil, Teoria dei numeri [1993] p.22. [21] Cfr. Bhaskara [1817] p. 348 sgg. Mi sono servito anche del commento di Konen e della esposizione di Thomas Heath in Diophantus of Alexandria [1910] pp. 277 sgg. [22] Sappiamo che questo è possibile per lo studio dell’equazio¬ne indeterminata ax + by = c. Anzi, la condizione dell’essere p e q primi tra loro è necessaria e sufficiente per la sua risolubilità. [23] Bhaskara non giustifica le sue affermazioni che sono state controllate ad esempio da Hermann Hankel e che si trovano anche nel libro citato di T. Heath [1910] p. 283 passim. [24] Questo metodo della discesa fu ritrovato da Genocchi anche in una dimostrazione di Campano di Novara (XIII sec.). Per varie indicazioni e per la dimostrazione di Campano cfr. E. Picutti, Angelo Genocchi e due priorità contestate di Fermat, Archimede, 1979, 3, pp. 178-182. [25] Cfr. Oeuvres de Lagrange, [1867], pp.671-731. [26] Cfr. A. Weil, Teoria dei numeri [1993] p. 25. [27] La scuola pitagorica per la radice quadrata di 2; Archimede per la radice quadrata di 3 ecc. Molto vasta è la letteratura sull’equazione di Pell-Eulero. In bibliografia sono stati indicati alcuni testi specifici dai quali poterne dedurre molti altri. [28] Ahmed Djebbar [2007], p. 201, definisce Leonardo Pisano “il più celebre di questi ‘traghettatori’ del sapere matematico”. [29] L. Pisano [1857] XII, 3 p. 175. Si veda anche il paragrafo 4.2.2.1 (pp. 92 sgg. di S. Maracchia [2008]). [30] Scrive Leonardo Pisano: “Altera vero questio a predicto magistero Johanne proposita fuit ut inveniretur quidam cubus numerus, qui cum suis duobus quadratis et decem radicibus in unum collectis essent viginti”. [31] Leonardo Pisano (Tre scritti inediti di Leonardo Pisano pubblicati da Baldassarre Boncompagni, [1856]) afferma preliminarmente, poiché è 10 l’altezza del rettangolo ACTD che ricostruisce il primo membro dell’equazione di misura 20, che la sua base TD maggiore dell’incognita, come risulta dalla costruzione è uguale a z; si ha pertanto x<2. Ma anche x>1 come si ottiene dall’equazione per sosotituzione. [32] Il procedimento seguito da Leonardo Pisano per ottenere questo risultato non è noto e sono state avanzate varie ipotesi al proposito. [33] BM 13901,12; cfr. a questo proposito S. Maracchia [2008] pp. 95-97. [34] Ivi, pp. 119-121, anche per i riferimenti alla Geometria di Erone. [35] Ecco cosa scrive Leonardo Pisano, dopo le prime righe introduttive rivolte a Federico II: “Meditai sull’origine dei numeri quadrati e trovai che essa proviene dalla successione ordinata dei numeri dispari”. [36] Liber Abaci, cap. XII ( [1857] pp. 283-284). [37] Ivi p. 349; il problema si trova anche nel Flos. [38] In verità, anche Cardano si serve dei numeri negativi per risolvere alcune equazioni così come aveva fatto d’altronde anche Bhaskara e prima ancora Brahamagupta (VI secolo). [39] Notiamo che, prima di Leonardo Pisano, anche lo Pseudo-Beda aveva trattato con i numeri negativi in Europa secondo M. Folkerts (Eine mathematische Schrift aus de Karolingerzeit, Sudhoffs, Archi. 56, 1972), cfr. anche J. Sesiano, The apparence of Negative Solutions in Mediaeval Mathematics (Archive for History of Exact Sciences, 32, 1985). Il lavoro di Leonardo Pisano era però molto più diffuso. [40] Liber Abaci, [1857], pp. 160 e 323 (il problema viene risolto due volte con metodi diversi; quello che qui si indica è il primo). [41] A questo proposito, cfr. S. Maracchia, “Sommare mele con cavalli: una strana esperienza matematica”, in La matematica e la sua didattica, Pitagora, Bologna, n. 3, 2007, pp. 372¬377. [42] A proposito di questa dimostrazione operata con numeri più piccoli di quelli usati da Archimede, Attilio Frajese scrive (Attraverso la storia della matematica, [1969], p. 301) “Possiamo qui effettivamente vedere l’atto di nascita della matematica moderna: non soltanto si è completamente riguadagnata la comprensione dell’opera degli antichi, ma si sorpassa, si supera, l’opera stessa” e, poco dopo, la possibilità di migliorare un risultato di Archimede “costituisce effettivamente il segno dei tempi nuovi che si avvicinano”. [43] J. Needham, [1981], p.166. [44] L’opera di Shen Kua, di notevole contenuto algebrico e geo¬metrico, fu scritta durante la dinastia Sung però nel 1086. In tale periodo, furono anche ristampati testi di Matematica tra cui (1115) l’antico Chiu-chang suan-shu (Arte del calcolo in nove capitoli, II sec. a. C. – I sec. d. C.) che per la Matematica cinese è stato paragonato con una certa esagerazione (il giudizio è il mio) agli Elementi di Euclide per quella greca. [45] Una commissione guidata da Giosuè Carducci fa risalire la nascita dell’Università di Bologna addirittura al 1088 ma in realtà la nascita è quella sopra indicata, allorché Federico Barbarossa con espressa ordinanza assegnò anche – come avevano già mostrato gli Arabi – un valore ufficiale al titolo raggiunto. Nella mescolanza internazionale dei docenti e degli studenti (si pensi, ad esempio, che nelle Università veniva concessa una certa protezione autonoma anche ai gruppi di studenti stranieri) legati da una stessa religione e da una stessa lingua scientifica, il latino, Federigo Enriques vede uno dei nuclei fondamentali dell’unità europea del Medio Evo. Per altre notizie e ipotesi sulla nascita della nostra Università cfr. L’università di Bologna nel passato e nel presente, Zanichelli, Bologna, 1919. [46] “Miracoloso espandersi” lo definisce Francesco Gabrieli (Biblioteca storica, Mondadori, vol. 29, p.78) che riporta di seguito anche alcune ipotesi del “miracolo”. [47] G. Volpe [1958] p. 244. [48] Naturalmente gli avvenimenti non furono così lineari: anzitutto le varie conquiste e i conseguenti assorbimenti avvennero in maniera differente a seconda dei vari popoli assoggettati (v. per questo i cap. VII¬XI del Maometto e le grandi conquiste arabe di Francesco Gabrieli). Inoltre ben presto, dopo la morte di Maometto, vi furono lotte di successione, frammentazioni talora definitive cui si innestarono anche le invasioni turche. Non c’è dubbio però che almeno tra gli studiosi vi furono scambi culturali favoriti, alla stregua del latino nel Medio Evo e nel Rinascimento in Europa, dall’unificazione della lingua araba come lingua colta. Ecco che cosa scrive, ad esempio, Carl Grimberg nella sua Storia universale ([1965] p. 40): “La dottrina di Maometto si diffuse dovunque, nella scia degli Arabi conquistatori, senza bisogno di alcuna coercizione, anche mercè la lingua araba che costituì un solido legame tra i diversi popoli dell’Impero. Siriani, Persiani, Egiziani e Berberi la impararono molto presto”. [49] C. Boyer, Storia della matematica [1976] p. 293.
|
