Simmetria e matematica 3
Gruppi di rosoniI gruppi diedrali e quelli ciclici
Si è visto che i gruppi finiti di isometrie del piano possono contenere solo rotazioni e riflessioni: sono detti " gruppi di roson i " mettendo in evidenza le figure più suggestive di cui sono gruppi di simmetria. In pratica, nell'arte o nella natura, si possono reperire numerosi esempi significativi di questi modelli. Ecco alcuni esempi nella Figura 2.10, ancora tratti dal bel libro di Slavik Jablan [4].
Lo studio dei gruppi di rosoni si può utilmente condurre attraverso i suoi " generator i " , vale a dire attraverso alcune isometrie particolari componendo le quali si ottengono tutte le isometrie del gruppo. Per esempio, è utile mettere in evidenza che i gruppi di simmetria dei poligoni regolari si possono generare con una sola rotazione ed una riflessione. Infatti, partendo dai poligoni con un solo lato (sic! ed un solo vertice) e da quello con due lati — utilmente introdotti per completezza anche se privi di evidenza geometrica — si hanno i gruppi di simmetria: |  Figura 2.10 Alcuni rosoni antichi e moderni |
D1={σ|σ2=id}
D2={σ, ρ|σ2=id, ρσ=σρ}
dove σ è una riflessione e ρ la rotazione di π. Si hanno poi: il gruppo di simmetria del triangolo equilatero, del quadrato.... dell'n-gono regolare:
D3={σ, ρ|σ2=ρ3=id, ρ2σ=σρ}
D4={σ, ρ|σ2=ρ4=id, ρ3σ=σρ}
Dn={σ, ρ|σ2=ρn=id, ρn-1σ=σρ}
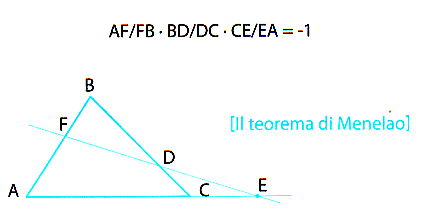
(e qui ρ denota la rotazione di 2π/n, Figura 2.11). Questi, i cosiddetti "gruppi diedrali" Dn, prendono concretezza dai loro modelli - i poligoni regolari - insieme ai quali vanno considerati.
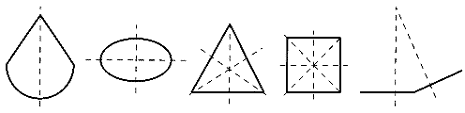
Figura 2.11 I poligoni regolari: modelli per i gruppi diedrali
Se la simmetria di riflessione invece manca, il gruppo ha un unico generatore ed è formato solo da rotazioni. In questo caso si dice che è un "gruppo ciclico":
C1={id}
C2={ρ|ρ2=id}
C3={ρ|ρ3=id}
C4={ρ|ρ4=id}
................
e forse non è inutile verificare su modelli grafici in che modo venga "persa" la simmetria di riflessione dei poligoni regolari (si veda la Figura 2.12). Il risultato attribuito da Hermann Weyl [7] a Leonardo da Vinci consiste proprio nello studio complessivo dei gruppi di rosoni:
Teorema (di Leonardo). Ogni gruppo di rosoni ha almeno un punto fisso ed è un gruppo diedrale oppure ciclico finito.
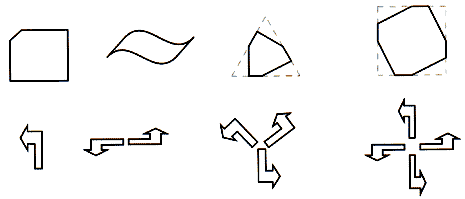
Fifura 2.12 Modelli per i gruppi ciclici
I gruppi dei fregi
Dai motivi matematici alla formalizzazione matematica
I gruppi dei rosoni, completamente caratterizzati dal teorema di Leonardo, sono i gruppi finiti di isometrie piane. E allora si pone naturalmente la domanda: quali sono i gruppi discreti di isometrie piane che non sono finiti? Naturalmente dovranno contenere al-meno una traslazione (e quindi infinite, ottenute per applicazione ripetuta di una di esse).
Una prima distinzione dei gruppi discreti di isometrie piane si conduce esaminando se tutte le traslazioni sono generate da una sola di esse, oppure da due: nel primo caso, i modelli di simmetria si estendono, indefinitamente ripetuti, in entrambi i versi di una direzione. Riempiono una striscia di piano e vengono detti "fregi", avendo in mente proprio quei fregi che in molti edifici ripetono un preciso motivo ornamentale. Nel secondo caso, quando tutte le traslazioni sono generate da due traslazioni indipendenti, si hanno i cosiddetti "gruppi cristallografici piani" (o "gruppi di mosaici", oppure anche "gruppi di carte da parati", come sono detti in ambienti e con scopi diversi), che si estendono in due direzioni non parallele a riempire ordinatamente tutto il piano.
Sia in un fregio che in un mosaico è presente un "modulo" che si ripete indefinitamente (in una oppure in due direzioni) che può possedere una propria simmetria interna. I criteri di classificazione in entrambi i casi tengono conto della compatibilità fra la simmetria interna, locale, del modulo e la simmetria globale dettata dalle traslazioni.
Non si tratta di considerazioni complicate, ma abbastanza lunghe e dettagliate. Inoltre obbligano a considerare molte nozioni e proprietà che fanno parte della teoria matematica dei gruppi: il libro di G.E Martin [6] tende proprio a esporre queste nozioni attraverso gli esempi che provengono dalla simmetria piana. Qui cerchiamo di illustrarle in maniera intuitiva dato che anche la sola enunciazione del risultato fornisce una forma di giustificazione e di plausibilità dotata di elementi costruttivi per lo studio della simmetria.
Intanto, ecco l'elenco dei possibili gruppi di fregi (sono in numero di 7) e dei loro modelli caratteristici, che possono assumere forma stilizzata oppure più evoluta, con i simboli che permettono di individuare il loro gruppo di simmetria, secondo il linguaggio illustrato in precedenza:
p111 ...PAPAPAPA...
p112 ...NONONON...
pmll ...MAMAMA...
pmm2 ...HOHOHO...
pmg2 ...∪∩∪∩∪∩∪∩....
p1m1 ... EEEEEE...
p1g1...PbPbPbPb...
L'analisi di alcuni dei numerosi (frammenti di) fregi che si trovano in natura o nelle rappresentazioni artistiche conduce a una consapevolezza del ruolo delle isometrie e del significato delle traslazioni. Per i matematici, tutto ciò rappresenta un importante intreccio fra gli aspetti formali e quelli più concettuali. Si vedano per esempio i fregi della Figura 2.13, che risalgono al periodo paleolitico.

Figura 2.13 Alcuni fregi primordiali (da Jablan [4])
La classificazione dei gruppi dei fregi si conduce in base alle isometrie che servono da generatori. Anche senza esplicitare questa classificazione, si può apprezzare la differenza che corre, dal punto di vista qualitativo, fra riconoscere un modello di simmetria e classificare tutti i possibili modelli, ed anche la difficoltà, dal punto di vista quantitativo, di determinare con precisione i sette gruppi dei fregi.
I gruppi cristallografici piani
Le restrizioni cristallografiche
Quando le traslazioni sono generate da due elementi indipendenti, i gruppi discreti di isometrie piane prendono il nome di " gruppi cristallografici piani", per mettere in evidenza che hanno avuto origine nell'ambito della classificazione dei cristalli. Ma sono conosciuti in letteratura anche con altri termini: sono "mosaici" quando si pensa alla produzione artistica — e vale la pena di sottolineare che nei mosaici dell'Alhambra di Granada gli artigiani arabi del XIII e XIV secolo hanno incorporato tutti i possibili gruppi di mosaici, anticipando nei fatti la loro completa classificazione. Oppure, quando si considera la loro capacità di coprire in maniera uniforme e regolare tutto il piano per semplice ripetizione di un modulo, vengono detti "gruppi di carte da parati".
Nel caso di questi gruppi, la richiesta di compatibilità fra le simmetrie locali del modulo e la simmetria globale della figura piana si esprime mediante un risultato fondamentale, detto di "restrizione cristallografica", che fissa la forma dei possibili reticoli piani lungo i quali il modulo può essere trasferito per traslazione.
Teorema (restrizione cristallografica). Le rotazioni dei mosaici possono avere periodo 1,2,3,4 oppure 6 (ma non 5).
In altri termini non possono esistere moduli di simmetria piana a forma pentagonale: ciò non significa che questa simmetria non possa presentarsi in natura — anzi sono noti molti organismi animali e vegetali di questo tipo — ma semplicemente che con essi non è possibile riempire in maniera uniforme tutto il piano.
Figura 2.14 Alcuni antichi mosaici
I criteri di classificazione dei gruppi dei mosaici riguardano poi altri caratteri geometrici della simmetria: la presenza di centri e assi di rotazione, l'appartenenza dei centri di rotazione a opportune rette e così via. Uno studio esaustivo e convincente di tutte le possibilità e della maniera con cui si organizzano richiede molto tempo, una buona dose di pazienza e una adatta disposizione. Alla fine si trove ranno 17 gruppi cristallografici piani e si tenderà a riconoscere il tipo di simmetria nei loro tipici modelli — come quelli della Figura 2.14, frequentemente presenti nelle manifestazioni artistiche e culturali. La classificazione completa dei gruppi di mosaici (un esempio della quale è nella Figura 2.15) sembra che sia stata effettuata per la prima volta nel 1891 da Evgraf Fédorov, in un articolo della società mineralogica russa, poi ripetuta in ambito matematico e resa nota da Paul Niggli e George Pólya nel 1924.
 Figura 2.15 Modelli dei 17 gruppi cristallografici piani
Figura 2.15 Modelli dei 17 gruppi cristallografici piani
Per concludere
E ora?
È tutta qui la matematica della simmetria per quanto riguarda le figure del piano? Quasi. Come al solito i matematici estendono e generalizzano le loro considerazioni. Ciò comporta naturalmente una maggiore difficoltà, che tuttavia è compensata dalla soddisfazione di una comprensione al tempo stesso più generale e più profonda, in parte facilitata dai casi che abbiamo appena esposti, che ne fornisco-no una guida concettuale.
La generalizzazione della simmetria delle figure piane porta a considerare la simmetria dei solidi dello spazio ordinario, tridimensionale, e poi a estendere il problema alle dimensioni superiori anche se il loro studio è, naturalmente, molto complicato. Lo è già nell ' ordinario spazio tridimensionale, dove le traslazioni sono generate da tre di esse che siano indipendenti: esistono 6 possibili isometrie e 230 gruppi discreti di simmetria – questi sono i veri e propri "gruppi cristallografici".
Vale la pena di osservare che, mentre si ritiene usualmente che esista un numero infinito di cristalli, il fatto che esista un numero finito, seppure grande, di gruppi cristallografici, spiega come i cristalli in realtà siano sottoposti a delle precise regole di formazione: i cristalli rappresentano precisamente tutte le possibili configurazioni tridimensionali che rispettano le restrizioni.
Quanto alle dimensioni maggiori di 3, il problema è stato riconosciuto come importante già da David Hilbert, che lo ha incluso in uno dei suoi famosi "23 problemi per il secolo futuro" presentati al Congresso Internazionale di Matematica del 1900. Pochi anni dopo la richiesta di Hilbert, è stato dimostrato che, in ogni dimensione, esiste soltanto un numero finito di gruppi di simmetria, senza tuttavia essere in grado di dire "quanti" sono. Il problema è combinatorialmente complicato: a metà degli anni '70 solo l'uso di un calcolatore ha permesso di stabilire che, nello spazio euclideo a 4 dimensioni, esistono 4783 gruppi discreti di simmetria. Per quanto ne so, non è stato ancora determinato il numero dei gruppi cristallografici per ogni dimensione superiore a 4 – ma molte ricerche sono in corso e ci sono alcuni, notevoli, risultati parziali.
Per quanto riguarda l'estensione dei concetti ad altri ambiti geometrici poi, perché limitarsi alle figure del piano o dello spazio euclidei? Molti mosaici del piano non euclideo iperbolico si possono apprezzare nelle splendide rappresentazioni del grafico C. Escher (si veda il sito http://www.mcescher.com/), a testimonianza ulteriore della connessione fra ricerca sistematica e intuito artistico che si trovano profondamente intrecciati nel tema della simmetria geometrica.
Bibliografia
 | Simmetria:una scoperta matematica
a cura di R. Betti, E. Marchetti, Luisa Rossi Costa
Polipress 2007 Politecnico di Milano, Milano pag.83 |
[1] Armstrong M.A., Groups and Symmetry, Springer, 1988
[2] Caglioti G., Simmetrie infrante, nella scienza e nell'arte, Clup, Milano 1983
[3] Dedò M., Forme. Simmetria e topologia, Zanichelli, Bologna 1999
[4] Jablan S.V, Teory of Symmetry and Ornaments, Beograd Mat. Institut n. 17, 1995 (reperibile in http://www-sbras.nsc. ru/EMIS/monographs/jablan/ )
[5] Lockwood E.H., Macmillan, R.H., Geometric Symmetry, Cambridge University Press, 1978
[6] Martin G.E., Transformation Geometry. An Introduction to Symmetry, Springer, 1982
[7] Weyl H., La simmetria, Feltrinelli, 1962
[8] www.ics.uci.edu/-eppstein/junkyard/sym.html