Sviluppi dell'Analisi funzionale nel Novecento
L’invito dell’Istituto Italiano per gli Studi Filosofici a parlare dell’opera di Renato Caccioppoli da un lato mi ha lusingato, dall’altro mi ha un po’ preoccupato, in quanto ritengo impresa non facile descrivere l’opera di un matematico dinanzi ad un pubblico costituito anche da filosofi e letterati.
D’altra parte, mi è sembrato opportuno cogliere questa rara occasione per tentare di far conoscere, almeno in piccola parte, il pensiero matematico ed alcune delle tematiche coltivate da Caccioppoli ad un pubblico non costituito da soli matematici.
Una prima parte dell’esposizione avrebbe descritto il contesto culturale e scientifico nel quale s’inserisce l’opera di Caccioppoli e cioè l’Analisi funzionale, così come sì è evoluta nel corso di questo secolo ad opera dello stesso Caccioppoli e d’altri grandi matematici come Hilbert, Banach, Leray, ecc.
La seconda parte avrebbe descritto in che modo l’opera di Caccioppoli si sia inserita in tale contesto scientifico e culturale.
Per questa seconda parte ho consultato Carlo Sbordone, che ha accettato volentieri di offrire la sua collaborazione.
Passiamo ora a tentare di descrivere ad un pubblico di varia cultura che cos’è l’Analisi funzionale. Riconosco di non essere la persona più adatta a poter svolgere questo compito, in quanto mi mancano alcuni tipi di conoscenze che forse sarebbero necessarie. Infatti, io non sono né uno storico della scienza, capace di illustrare lo sviluppo storico, né un filosofo della scienza, capace di illustrare il senso filosofico di tali concetti. Sono semplicemente un matematico, che lavora, di fatto, con gli oggetti dell’Analisi funzionale e che cerca di dare al pubblico esterno un’idea di quello che sa.
Mi scuso, perciò, se la mia esposizione sarà notevolmente ridotta rispetto a quanto promesso dal titolo e mi auguro che essa non risulti del tutto incomprensibile per i non matematici. Allo scopo di evitare, però, che la volontà d’essere comprensibili porti all’imprecisione, vorrei fare una breve premessa.
Gli “enti matematici” possono essere considerati da tre punti di vista. Un primo punto di vista è quello secondo il quale gli enti matematici esistono in sé; cioè, ad esempio, esistono effettivamente l’insieme di tutti i numeri interi, l’insieme di tutte le rette, dei cerchi, dei quadrati.
Un secondo punto di vista concerne gli oggetti fisici che rappresentano gli enti matematici.
Un terzo punto di vista riguarda poi il mondo delle formule, degli assiomi, del linguaggio tecnico mediante il quale questi enti vengono descritti.
Questi tre mondi sono strettamente collegati fra di loro ma non sono la stessa cosa.
Fatta questa premessa, a mio avviso, le varie semplificazioni didattiche che si possono fare non contrastano più con quell’onestà intellettuale che induce a non nascondere al pubblico, per amore di chiarezza o semplicità, quelle che sono le diversità.
Volendo accennare alla diversità che sussiste tra il mondo degli enti matematici e quello delle sue rappresentazioni fisiche, possiamo riflettere su di un esempio classico, già noto nell’antichità, che è quello della diagonale di un quadrato.
Tutti sanno che cos’è il quadrato e che cos’è la sua diagonale. Tuttavia, proprio in questo “tutti sanno c’è il punto delicato in cui compare la differenza tra rappresentazione fisica e quadrato ideale, che è l’oggetto proprio dello studio matematico.
Infatti, se disegno un quadrato, ognuno si accorge che esso è un’immagine approssimativa del quadrato ideale della Matematica; ma anche se fossi un ottimo disegnatore ed avessi squadre, compassi ed una carta perfetta, certamente eseguirei immagini più precise, ma non disegnerei mai il vero quadrato della Matematica.
Vi sono alcune differenze essenziali tra i quadrati disegnati ed il vero quadrato: basta riflettere su quello che è stato uno dei teoremi che a suo tempo destò maggiore scalpore nella Matematica antica. Cioè il teorema che afferma che “la lunghezza della diagonale non è commensurabile con la lunghezza di un lato, nel senso che non possiamo mai trovare due numeri interi tali che il rapporto tra la lunghezza di un lato e quella di una diagonale sia uguale al rapporto di questi due numeri interi”. Questo è stato uno dei teoremi fondamentali da cui è nata la teoria dei numeri irrazionali.
Per quanto possa essere raffinata la nostra capacità di disegno e di misura, non sarà mai tanto raffinata da poter distinguere un numero razionale da un numero irrazionale. Quindi, questo è un esempio di una proprietà centrale del concetto matematico di quadrato che non ha nessun riscontro in quelle che sono, invece, le proprietà visibili dei quadrati disegnati. Perciò, quando si parla d’enti matematici, occorre ricordare la differenza fra l’ente matematico in sé e le sue rappresentazioni fisiche. Ignorare questa differenza significa anche non capire perché, ad esempio, ai matematici piacciono tanto certi teoremi di “esistenza” di soluzioni di cui l’”utente” pratico della Matematica non sa in genere cosa fare e che magari ritiene inutili.
Tuttavia questi teoremi ci dicono che, nel mondo ideale degli enti matematici, certi enti hanno proprietà importanti anche se poco o per nulla visualizzabili, come per nulla è visualizzabile l’irrazionalità del rapporto tra lato e diagonale.
Ciò premesso, possiamo tentare di dare una qualche idea di che cos’è l’Analisi funzionale.
Cimmino ha parlato dell’importanza delle ricerche di Caccioppoli su “gli spazi ad infinite dimensioni”, “gli spazi dell’Analisi funzionale”, “i funzionali lineari” e così via. Vogliamo tentare di discutere un po’ sulla natura di questi spazi funzionali, cominciando col descrivere il concetto di “funzione”.
L’idea di funzione intuitivamente è abbastanza semplice: si dice che una certa grandezza è funzione di un’altra grandezza, se i valori della prima sono univocamente determinati dai valori dell’altra. Facciamo un esempio. Se noi pensiamo alla temperatura massima e minima registrata a Pisa in un certo giorno, vediamo che l’una e l’altra sono “funzioni” del giorno considerato. Questo collegamento funzionale viene correttamente rappresentato e visualizzato attraverso i grafici. Anche chi non è matematico avrà visto certamente che, quando si vuole indicare l’andamento di un fenomeno, si traccia una retta sulla quale sono riportati, in una certa scala, i valori della variabile indipendente (asse delle x, o primo asse cartesiano), poi una seconda retta, perpendicolare alla prima, su cui vengono riportati i valori della variabile dipendente (asse delle y o secondo asse cartesiano), infine si disegna il grafico che è caratterizzato dalle seguenti proprietà: il grafico è una curva tale che, se si prende un punto P sul grafico, si abbassa da P la perpendicolare sul primo asse e se ne indica il piede con x (ascissa di P), si abbassa poi da P la perpendicolare al secondo asse e s’indica con y (ordinata di P), y rappresenta il valore preso dalla variabile dipendente quando la variabile indipendente prende il valore x.
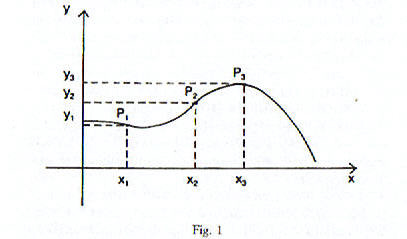
Tale curva rappresenta una funzione che dà un’idea di come siano cresciuti o diminuiti i profitti (o le perdite) della società.
Lo stesso si può dire, per esempio, per la temperatura corporea di un ammalato, (credo che chiunque abbia visitato un amico in ospedale avrà visto, in certe tabelle, una curva che poteva rappresentare l’andamento della temperatura corporea, un’altra che rappresentava l’andamento della pressione, ecc.).
Questo tipo di rappresentazione grafica delle funzioni fa ormai parte della cultura comune e quindi non richiede ulteriori illustrazioni. In quale rapporto stanno queste figure che noi troviamo su tutti i giornali, su tutte le tabelle, con l’idea matematica di funzione? Direi che più o meno stanno negli stessi rapporti in cui le figure che rappresentato un quadrato stanno con l’idea matematica di quadrato.
Quindi l’Analisi Funzionale tratta delle funzioni, un concetto matematico di cui le più semplici rappresentazioni sono questi grafici che abbiamo visto.
Vediamo ora come l’Analisi funzionale tratta queste funzioni. In generale, l’Analisi funzionale non si limita a trattare una funzione per volta, o un numero finito di funzioni per volta.
Questo è un lavoro che fu già sviluppato, nel calcolo infinitesimale classico, da Newton, Leibniz, ecc. Nell’Analisi funzionale del XX secolo, c’è, di nuovo, l’interesse a considerare una famiglia infinita di funzioni e ad organizzare in qualche modo, in maniera da poter studiare le proprietà di questa famiglia organizzata, che prende il nome di “spazio funzionale”.
Lo studio degli spazi funzionali può essere condotto a vari livelli. Il livello più semplice è quello in cui la famiglia molto ampia di funzioni viene considerata come spazio metrico. Vediamo subito cosa intendiamo per “spazio metrico di funzioni”. Vuol dire che elementi di questo spazio saranno infinite funzioni. Per esempio tutte le funzioni che possono essere rappresentate (più o meno bene!) dai grafici di cui abbiamo parlato, sono funzioni reali di variabile reale.
In questa famiglia infinita di funzioni si tratta di inserire una qualche nozione di “distanza” cioè un qualche numero che dica “quanto” una funzione differisce da un’altra.
Ci sono diversi modi in cui su uno stesso insieme d’oggetti si possono determinare le distanze, e questo non contrasta col buon senso comune. Ad esempio, per misurare la distanza tra due città, possiamo dire quanto distano in linea d’aria, oppure quanto distano seguendo la strada asfaltata più breve possibile, oppure quanto costa il biglietto ferroviario per andare da una all’altra in treno, ecc. Ciascuna di queste quantità, ognuna diversa dall’altra, fornisce un ragionevole tipo di distanza tra due città.
Quindi, uno dei primi fenomeni che il buon senso suggerisce e la teoria Matematica degli spazi metrici considera, è che possono esserci degli spazi formati dagli stessi elementi, in cui sono definiti diversi tipi di distanze. Vediamo quali sono le più semplici distanze che possono stabilirsi tra due funzioni.
Volendo visualizzare la definizione, conviene considerare allo stesso tempo due grafici. Una definizione di distanza che appare ragionevole consiste nel prendere il massimo scarto tra le due funzioni. In altre parole, si considerano tutte le differenze tra i valori dell’una ed i valori dell’altra e si vede qual è il punto in cui la distanza è massima.
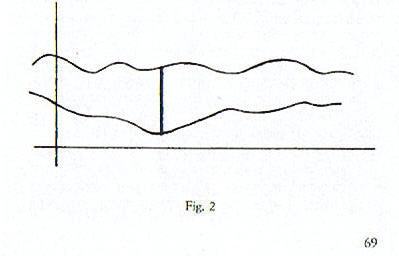
Ad esempio, se queste fossero due temperature, massima e minima, o due temperature rilevate in due città diverse, ci si potrebbe chiedere quale sia stato il giorno in cui la temperatura di una città era più lontana dalla temperatura dell’altra o la temperatura massima più lontana dalla minima. Ed allora avremmo una prima possibile distanza, che graficamente sarebbe rappresentata dal segmento che ho tratteggiato in fig. 2. Accanto a questo tipo di distanza, si può pensare ad una distanza media, la temperatura di una città è poco o molto diversa dalla temperatura dell’altra. Ed allora, invece di misurare la lunghezza di quel segmento, converrebbe misurare l’area racchiusa tra i due grafici (fig.3), ottenendo così un altro tipo di distanza.
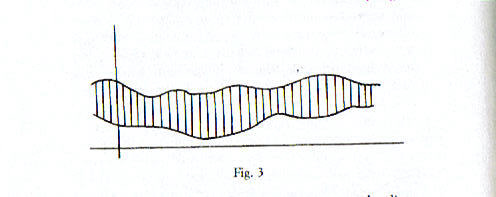
Accanto a queste, poi, si possono pensare molte distanze intermedie, quale il cosiddetto “scarto quadratico medio” che si trova, per così dire, a metà strada fra la distanza calcolata come massima differenza fra due funzioni e la distanza calcolata come differenza tra due funzioni.
Comunque, già le prime due sono distanze abbastanza significative ed importanti nello studio degli spazi funzionali e, nello stesso tempo, abbastanza ben visualizzabili.
Dunque, gli spazi funzionali sono insiemi di funzioni organizzate mediante la definizione di una distanza; in modo più raffinato, si potrebbe parlare di “topologia”, però già gli spazi muniti di distanza rappresentano una classe importante, molto ampia, con molte applicazioni in Matematica pura ed applicata.
Qual è l’interesse di tali spazi?
Evidentemente, se di tali spazi avessimo solo la definizione, avremmo un modo per rappresentare bene certi fatti intuitivi, ma non avremmo ancora una teoria matematica elaborata.
La grande opera dei matematici del XX secolo è stata precisamente quella di studiare la struttura geometrica di tali spazi, di vedere che in questi spazi i cui elementi sono funzioni, si possono trasferire molti concetti, come quello di “geodetica” o quello di “linea di livello”, propri della geometria elementare.
Ciò ha creato, da un lato, un certo bagaglio di teorie, dall’altro, una specie d’intuizione spaziale generale, per cui il matematico di talento, ad un certo punto, vede questi spazi ad infinite dimensioni con la stessa naturalezza ed in modo abbastanza simile a quello con cui il matematico classico vedeva le figure del piano e dello spazio ordinario. Poi, naturalmente, accanto a questa visone più intuitiva, c’è la formalizzazione della teoria degli spazi metrici, che avviene attraverso una serie d’assiomi abbastanza naturali ed anche attraverso un formalismo più o meno complicato, a seconda del livello di raffinatezza che si vuole raggiungere nella teoria.
Anche di questi assiomi vi sono alcuni che sono riservati agli specialisti, ma vi sono altri che, invece, possono essere perfettamente descritti dinanzi ad un qualsiasi pubblico. Ad esempio, i tre assiomi fondamentali dello spazio metrico sono assiomi perfettamente naturali, collegabili a qualsiasi idea di distanza o di differenza. Il primo assioma è la cosiddetta “proprietà triangolare” cioè la proprietà che afferma che: “dati tre elementi a, b, c, la distanza di a da c è minore o uguale alla somma delle distanze di a da b e di b da c”. Questo è un assioma coerente con ogni ragionevole idea di distanza. L’altro assioma è quello che afferma che: “un elemento ha distanza nulla da se stesso” ed è anche questo appare ragionevole. Il terzo assioma è quello più difficile da accettare ed, infatti, in alcune teorie viene omesso; esso afferma che: “la distanza di a da b è uguale alla distanza di b da a”. Questo assioma è naturale se si pensa ad una geometria di strade piane; ma potrebbe essere di meno se si pensasse ad un sistema di strade in salita e in discesa e si assumesse come “distanza” il tempo che occorre per andare dal punto a al punto b.
Si possono sviluppare teorie matematiche ragionevoli, sia sulle “distanze simmetriche” che sono quelle più utilizzate, sia sulle “distanze asimmetriche” anche se queste sono meno utilizzate.
Le cose diventano un po’ più complicate allorché si comincia a vedere qual è la “dimensione” di questi spazi funzionali.
Diamo, adesso, un’idea intuitiva del concetto di “dimensione”. Se consideriamo una curva, essa è una figura unidimensionale. Il concetto di “unidimensionale” può essere reso in questo modo: se si prende una curva, ad esempio, lunga un metro e si vuol dividerla in parti di curva lunghe un cm, allora basta dividerla in cento parti. Se invece si prende una superficie di un metro quadrato e la si vuol decomporre in parti di un centimetro quadrato, si è costretti a decomporla in diecimila parti. Se si prende un cubo di un metro cubo e lo si vuol dividere in parti di un centimetro cubo, si è costretti a dividerlo in un milione di parti.
Questo fatto viene formalizzato dicendo che “la dimensione della curva è uno, la dimensione della superficie è due, la dimensione del cubo è tre”.
Lo stesso discorso potrebbe essere ripetuto a proposito degli spazi funzionali e si dimostra facilmente che questo tipo di dimensione, detta “dimensione di Hausdorff”, per gli spazi funzionali più interessanti è infinita.
La considerazione di spazi di dimensione infinita comporta una serie di problemi, per cui, da certi punti di vista, essi sono molto simili agli spazi di dimensione finita; sotto altri aspetti, presentano invece caratteristiche paradossali, che richiedono un’analisi un po’ più accurata di quella data dalla pura e semplice trasposizione dal finito all’infinito. Si entra così nel mondo dei paradossi dell’infinito e quindi in un campo in cui l’intuizione matematica, nata dall’osservazione fisica, deve essere controllata e guidata da accortezze di tipo logico, per evitare di pervenire ad affermazioni contraddittorie.
L’arte di persone come Caccioppoli è in fondo la capacità, eccezionale in lui, di muoversi in questi spazi di dimensione infinita con estrema sicurezza intuitiva, comprendendo a prima vista dove l’analogia col finito funziona e dove l’analogia con gli spazi di dimensione finita cessa di funzionare.
Ricordo qualche conversazione che ho avuto con Caccioppoli, che purtroppo ho conosciuto solo per un numero esiguo, anche se decisivo, di anni della mia formazione e ricordo, appunto, che rarissime volte, per discutere di Matematica, egli chiedeva una lavagna. In genere si trovava in un caffè, in un bar, in una trattoria ed egli prendeva un foglio di carta, dicendo: “le cose vanno così…”, tracciava due o tre segni abbastanza sommari, univa a questi segni un discorso sintetico, ma estremamente profondo e dava, in tempi brevi, l’idea come in realtà stavano le cose a proposito di un certo problema.
Ho esposto, così, uno dei motivi che hanno, negli ultimi tempi, reso difficile la piena comprensione dell’opera di Caccioppoli in campo internazionale. Il carattere estremamente sintetico del suo pensiero, che contrastava con le abitudini molto più analitiche, molto più sistematiche che sono andate, in parte per buone ragioni, in parte per nostra sfortuna, prevalendo nell’analisi contemporanea.
Oltre ai problemi relativi allo studio degli spazi funzionali, vorrei ricordare uno dei problemi in cui è stata fondamentale l’opera di Caccioppoli, precisamente quella che viene oggi chiamata “teoria geometrica della misura”, anche perché è stato il campo in cui ho avuto con lui intensa collaborazione scientifica.
Come nascono i problemi dell’Analisi funzionale relativi alla teoria geometrica della misura?
I problemi dell’Analisi funzionale nascono in questo modo. Se disegniamo una figura piana come quella in fig. 4, è abbastanza naturale dire qual è il suo perimetro.
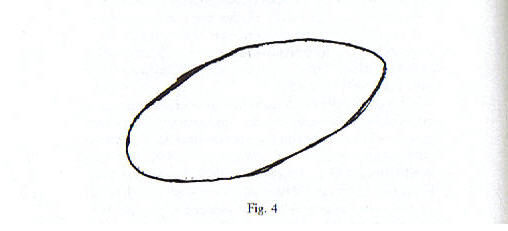
Gli spazi funzionali più interessanti in Matematica hanno il difetto che, dentro lo spazio, occorre porre anche figure e curve che non siano continue e che siano tracciate abbastanza male. Ad esempio, accanto a quelle curve continue che ho disegnato, per avere uno spazio funzionale “completo”, di agevole maneggio, si devono mettere anche molte curve discontinue, anche se poco disegnabili. Si dovrebbero, così, mettere curve del tipo disegnato in fig.4 e si dovrebbero mettere anche curve continue a tratti; poi, non contenti delle curve continue a tratti con un numero finito di salti, si dovrebbero anche mettere curve continue a tratti con un numero infinito di salti, sparsi nei modi più strani, fino a che la curva diventi non più disegnabile, salvo che non si voglia fare un disegno assolutamente incomprensibile (fig. 5).

Uno dei prezzi da pagare, per fare dell’Analisi funzionale efficiente, con bei teoremi, è la completezza degli spazi, che debbono contenere, accanto alle funzioni, curve e figure pochissimo regolari.
Una volta inserite funzioni, curve e figure pochissimo regolari, quali ad esempio le “funzioni misurabili” secondo Lebesgue, dette così dal nome del matematico H. Lebesgue che è stato uno dei grandi pionieri nello studio di queste funzioni con scarsissima regolarità (prima di lui c’erano stati gli studi di Dirichlet, Cantor, ecc.) è stato possibile dare una ragionevole definizione della quadratura delle superfici.
Anche in questo caso, una certa idea credo possa essere data anche al non matematico, in un modo molto semplice.
Se desidero misurare il perimetro della curva in figura 4 e dispongo soltanto di una riga numerata, ma non di un filo con cui seguirne il contorno, che cosa farò per valutare quel perimetro?
Cercherò di trovare dei poligoni i cui lati sono misurabili con la mia riga numerata ed approssimerò quella figura mediante poligoni e mi chiederò, poi, quanto quel poligono sia vicino alla figura di cui devo valutare il perimetro.
Qui l’idea semplicissima, però estremamente feconda, di Caccioppoli è stata quella di misurare la distanza tra il poligono e la figura con l’area dell’insieme differenza, quindi la distanza tra il poligono e la figura sarà l’area tratteggiata in figura 6.
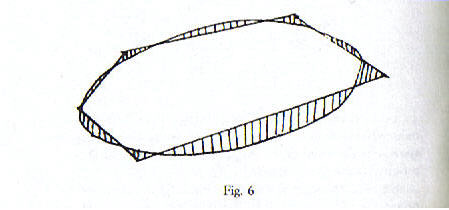
Quindi, per avere un’idea del perimetro, bisognerà prendere una successione di poligoni, tale che quell’area diventi sempre più piccola e questi daranno una serie di valori approssimati del perimetro.
Qual è il punto più delicato? Il punto più delicato è che io posso approssimare “in area” quella figura in modi diversi, anche con poligoni che, in realtà, hanno un perimetro ingiustamente grande, ed io posso sempre divertirmi, per esempio, a prendere, accanto a poligoni che seguono abbastanza bene l’andamento della figura, anche altri poligoni vicinissimi in area ma con perimetro molto più grande. A tale scopo, infatti, basta “arricciare” un poligono – purtroppo la sequenza dei disegni non si presta ad una rappresentazione statica con una figura data – e fargli avere dei perimetri giganteschi (fig.7).
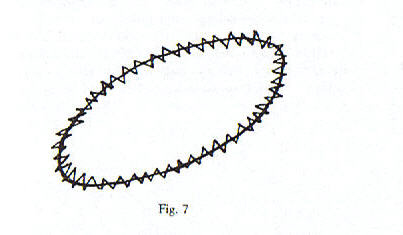
Il problema, allora, non è semplicemente quello di prendere una successione di poligoni che approssimi una certa figura, ma di considerare tutte le successioni di poligoni che approssimano quella figura e di prendere, tra i limiti dei perimetri, il più piccolo valore, quello, appunto, che si suole chiamare “il minimo limite dei perimetri dei poligoni approssimati”.
Questa è un’idea abbastanza semplice, che però rappresenta un notevole passo in avanti, un notevole punto di chiarificazione nello studio della nozione di perimetro e quindi nell’elaborazione della teoria geometrica della misura.
Per vedere qual era la differenza tra questa idea di Caccioppoli e le idee, pure estremamente valide, di una persona come Lebesgue, nel misurare l’area, basta osservare che, mentre Lebesgue, Peano ed altri matematici, tutti di primissima grandezza, si sono soprattutto preoccupati del fatto che il poligono approssimasse puntualmente la figura, invece Caccioppoli vide che la teoria risultava molto più maneggevole ed elegante se ci si accontentava soltanto dell’approssimazione in area, che non escludeva nemmeno poligoni molto lontani, nel senso della massima distanza, dalla figura considerata. Ad esempio, la teoria di Caccioppoli non impediva di aggiungere a questi poligoni dei quadratini molto lontani dalla figura (fig. 8).
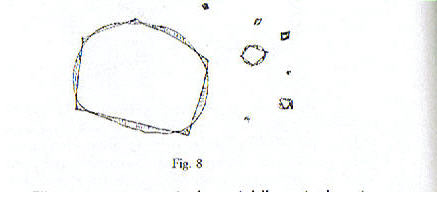
Ciò comportava una serie di elementi della teoria che poi sono stati tra le idee ispiratrici di quella che è la moderna teoria geometrica della misura, il moderno studio dei problemi isoperimetrici, delle superfici di area minima, ecc. Questa è stata, non dico la più grande idea di Caccioppoli, ma comunque quella sulla quale personalmente ho avuto più occasioni di riflettere.
Fra l’altro, questa teoria geometrica inquadra altrettanto bene superfici “indisegnabili” e superfici di area minima che hanno modelli fisici molto semplici. Per esempio le bolle di sapone si dispongono secondo superfici minimali. Le bolle di sapone costituiscono solo un “gioco da ragazzi”; tuttavia lo stesso tipo di equazione che regola le bolle di sapone, regola molte strutture sottili, quali ad esempio l’involucro di un aerostato, un tendone di circo, le volte di cemento di spessore molto sottile e così via.
Con questo ho cercato di dare un’idea intuitiva del tipo di questioni su cui si è cimentato, con grande successo, Renato Caccioppoli, nel corso della sua attività scientifica, del suo pensiero, aperto alle suggestioni che provengono dalle scienze sperimentali e dalla tecnica, ed insieme capace della più audace astrazione matematica.
