Un approccio statistico alla congettura di Goldbach
Prima di parlare della congettura, è necessario ricordare cosa sono i numeri primi. Stando alla definizione elementare di numero primo, esso è un numero divisibile soltanto per se stesso e per 1. In base a tale definizione, anche 1 sarebbe un numero primo ma, per questioni di ordine pratico (che qui non approfondiremo) si tende a escludere 1 dalla lista dei numeri primi.
La definizione normalmente accettata di numero primo è, pertanto, la seguente:
È numero primo un qualsiasi numero naturale maggiore di 1 divisibile soltanto per se stesso e per 1.
Come vedremo più avanti, il fatto di includere o meno tra i numeri primi il numero 1, non cambia la sostanza dei risultati della nostra indagine sulla congettura di Goldbach.
La congettura, così come la conosciamo oggi, afferma:
Ogni numero pari maggiore di 2 può essere espresso come somma di due numeri primi (anche uguali).
Ma come nasce tale affermazione? Christian Godbach (1690-1764), matematico tedesco e professore all'Accademia delle Scienze di San Pietroburgo, nel 1742 propose all'eminente matematico Eulero (1707-1783) la seguente congettura:
Ogni numero maggiore di 5 può essere espresso come somma di tre numeri primi.
Che poi Eulero riformulò nella seguente versione equivalente:
Ogni numero pari maggiore di 2 può essere espresso come somma di due numeri primi.
Oggi distinguiamo le due formulazioni, quella di Eulero è detta congettura forte di Goldbach mentre quella originale è chiamata congettura debole di Goldbach.
In particolare, l'aggettivo forte deriva dal fatto che, se vera, anche l'altra lo sarebbe di conseguenza, infatti è sufficiente aggiungere il numero primo 3 ad ogni numero pari a partire dal 4. Inoltre possiamo anche sottolineare che la congettura proposta inizialmente da Goldbach è equivalente alla versione forte poiché, banalmente, se per i numeri dispari è sufficiente aggiungere 3, per quelli pari è sufficiente aggiungere 2 (sempre per numero pari maggiore o uguale a 4).
Ma veniamo alla nostra indagine statistica. Come ogni congettura, si tratta di una supposizione fondata su indizi e apparenze probabili; si differenzia pertanto da un teorema in quanto non è dimostrabile (almeno finora) in modo inconfutabile. Molti matematici ritengono che questa congettura sia vera basandosi su considerazioni di tipo statistico, cosa che anche noi faremo qui di seguito. La differenza rispetto a quanto già fatto da altri è che lo faremo in modo talmente semplice, da essere compreso anche da chi ha poca dimestichezza con il linguaggio matematico.
Iniziamo con l'affrontare il problema "in negativo", ovvero verifichiamo quali sono le ipotesi per le quali sarebbe sicuramente "non vera" la congettura:
1a ipotesi: sarebbe sicuramente "non vera" se i numeri primi fossero "finiti", ma è stato dimostrato che essi sono infiniti [1].
2a ipotesi: sarebbe sicuramente "non vera" se, chiamando P1 un qualsiasi numero primo e P2 il numero primo immediatamente successivo, si verificasse almeno in un caso per cui: (P2–P1)/P1>1 (perché in questo caso il numero pari (P2+1) non verificherebbe l'assunto). Detto in altri termini: se, considerato un qualsiasi numero primo, quello immediatamente successivo vale più del doppio, il numero pari immediatamente successivo al numero primo più grande non potrebbe essere scritto come somma dei due numeri primi [2].
Fermo restando che, pur se si riuscisse a dimostrare l'inesistenza della 2a ipotesi, ciò non dimostrerebbe quanto formulato dalla congettura, pur tuttavia: minore è la probabilità che la 2a ipotesi sia vera, più è alta la probabilità che lo sia la congettura.
Qui di seguito, quindi, andremo ad indagare se, all'aumentare del valore dei numeri, la 2a ipotesi abbia meno probabilità di verificarsi. Espresso in termini matematici verificheremo se all'aumentare del valore di P1, il rapporto (P2–P1)/P1 diminuisce. Se ciò si verificasse, allora all'aumentare del valore dei numeri, aumenta la densità di presenza dei numeri primi rapportata al maggior valore dei numeri considerati.
Prendiamo in considerazione l'intervallo dei numeri primi da 2 a 10.243 e costruiamo la seguente tabella (la tabella completa è riportata nel foglio di calcolo Excel allegato):
| N. prog. | N. primi | Differenza tra N. primi | Rapporto | Media dei rapporti |
| A | B | C | C/B | |
| 1 | 2 | |||
| 2 | 3 | 1 | 0,5 | |
| 3 | 5 | 2 | 0,6667 | |
| 4 | 7 | 4 | 0,4 | |
| 5 | 11 | 2 | 0,5714 | 0,5345 |
| 6 | 13 | 4 | 0,1818 | |
| 7 | 17 | 4 | 0,3077 | |
| 8 | 19 | 2 | 0,1176 | |
| 9 | 23 | 4 | 0,2105 | 0,2044 |
| ... | ... | ... | ... | ... |
| 1.251 | 10.24 | 20 | 0,002 | 0,0012 |
Come si può verificare (in maniera puntuale nel foglio di calcolo Excel allegato) le medie indicate nell'ultima colonna hanno, all'aumentare del valore dei numeri, il seguente andamento:
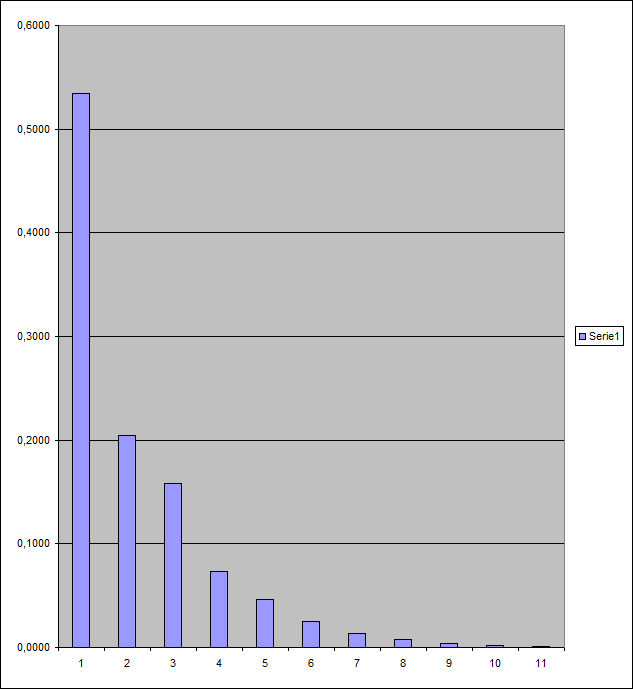
| 0,5345 | 0,2044 | 0,1579 | 0,0736 | 0,0464 | 0,0248 | 0,0136 |
| 0,0076 | 0,0042 | 0,0022 | 0,0012 |
Questi valori danno luogo al seguente grafico:
La tabella ed il grafico sopra riportati fanno verificare empiricamente che, all'aumentare del valore di P1, diminuisce tendenzialmente il valore del rapporto (P2–P1)/P1, quindi ci si allontana sempre di più dalla possibilità del verificarsi della 2a ipotesi.
Come si evince dalla tabella e, ancor meglio, dal foglio di lavoro Excel allegato, il rapporto (P2-P1)/P1 non è strettamente decrescente: a volte diminuisce, poi aumenta, poi diminuisce di nuovo; ma quello a cui siamo interessati è l'andamento tendenziale, quindi abbiamo proceduto, nel determinare gli intervalli su cui calcolare la media, con una scala che raddoppia ad ogni intervallo.
Dunque da questa nostra piccola indagine statistica si conclude che, all'aumentare del valore dei numeri presi in considerazione, la differenza tra un qualsiasi numero primo e quello immediatamente successivo, non varia significativamente, quindi la densità di presenza di numeri primi, se rapportata al valore sempre maggiore dei numeri presi in considerazione, tende ad aumentare. L'aumento di tale densità, fa sì che il valore del rapporto indicato nella seconda ipotesi diminuisca tendenzialmente all'aumentare del valore di P1. E tutto ciò rende sempre più probabile il verificarsi della congettura per valori sempre più alti dei numeri presi in considerazione [3].
Note
[1] Vedere la dimostrazione di Euclide risalente a più di 2000 anni fa.
[2] Ciò è vero, ovviamente, se non consideriamo il numero 1 nell'elenco dei numeri primi, se invece lo volessimo includere in tale elenco, la formula indicata sopra dovrebbe diventare la seguente. (P2–(P1+1))/P1>1 (in questo caso, il numero pari (P2–1) non verificherebbe l'assunto).
[3] Chi volesse provare a fare la stessa indagine includendo tra i numeri primi anche il numero 1 (modificando i termini del rapporto come indicato alla nota precedente) noterà che perverrà alle stesse conclusioni qui esposte.