Sistemi dinamici e caos deterministico
|
Negli ultimi venti anni, si è parlato molto dei metodi e dei risultati matematici che hanno portato alla definizione di caos deterministico. Questi risultati sono stati ottenuti nell'ambito di quel settore della Matematica noto come Teoria qualitativa dei sistemi dinamici e sono stati stimolati dall'esigenza di rappresentare, mediante modelli matematici, i sistemi reali che evolvono nel tempo come il moto dei pianeti, le oscillazioni di un pendolo, il flusso delle correnti atmosferiche, lo scorrere più o meno regolare dell'acqua in un fiume, il numero di insetti che anno dopo anno popolano una certa regione, l'andamento giornaliero dei prezzi delle azioni nei mercati finanziari e così via.
L'apparente contraddizione (o paradosso) contenuto nel termine caos deterministico, ha molto incuriosito anche il pubblico dei non specialisti. I modelli matematici di tipo deterministico vengono in genere associati all'idea di fenomeni regolari, prevedibili, che si ripetono nel tempo, mentre il termine caotico viene riferito a situazioni caratterizzate da assenza di regole e da imprevedibilità. La scoperta del caos deterministico spezza questa dicotomia, in quanto mostra come modelli matematici deterministici (cioè privi di ogni elemento aleatorio nelle equazioni che li definiscono) sono in grado di generare andamenti estremamente complessi, sotto molti aspetti imprevedibili, tanto da risultare quasi indistinguibili da sequenze di eventi generati attraverso processi aleatori.
Scopo di questo articolo è di descrivere a grandi linee lo sviluppo storico e introdurre un minimo di terminologia della teoria dei sistemi dinamici, facendo in particolare riferimento alla sua trattazione più moderna, nota come qualitativa (o topologica).
La teoria dei sistemi dinamici è stata anche chiamata la Matematica del tempo. In effetti, anche nel linguaggio comune, il termine dinamico si riferisce a processi che producono cambiamenti, ossia evolvono nel corso del tempo. Cerchiamo quindi di capire come si può simulare, matematicamente, l'evoluzione temporale di un sistema reale.
Innanzi tutto, occorre individuare un certo numero di grandezze misurabili, cioè espresse mediante numeri reali x1, x2, ..., xn, che permettano di identificare lo stato ossia la configurazione ad un certo istante t, del sistema che si vuol esaminare. Tali grandezze sono dette variabili di stato. L'insieme dei loro valori definisce univocamente lo stato del sistema ad un dato istante t, espresso dal vettore a n componenti:
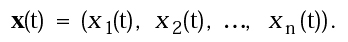
In molti problemi di Meccanica, lo "stato del sistema" in un dato istante è determinato dall'insieme delle posizioni e delle velocità dei corpi che lo costituiscono. Ad esempio, per un pendolo che oscilla, lo stato ad un certo istante è dato dall'angolo della cordicella rispetto alla verticale e dalla velocità della pallina ad essa appesa. In un ecosistema, lo stato può essere caratterizzato assegnando il numero di individui per ciascuna specie animale che ne fa parte; in un mercato finanziario, i prezzi delle azioni.
Pertanto, a prescindere dalla natura del sistema considerato, il suo stato ad un certo istante viene rappresentato da un vettore x appartenente ad Rn che, com'è noto, può essere pensato come un punto geometrico riferito agli assi di un riferimento cartesiano, in cui le coordinate corrispondono ai valori delle variabili di stato. Così, lo stato di una popolazione di insetti può essere rappresentato in uno spazio unidimensionale (una semiretta, dato che la numerosità della popolazione può assumere solo valori non negativi). Lo stato di un pendolo semplice è rappresentato da un punto in uno spazio bidimensionale (un piano cartesiano) riportando sugli assi il valore dello spostamento angolare rispetto alla verticale e il valore della velocità angolare. Lo stato di un sistema ecologico, in cui sono presenti 4 specie, è rappresentato da un punto in uno spazio a 4 dimensioni. Lo stato di un mercato finanziario è un punto, in uno spazio le cui dimensioni sono tante quanti i titoli trattati. L'insieme di tutti i possibili vettori di stato è detto spazio delle fasi del sistema dinamico.
La variabile t, utilizzata per misurare il tempo che scorre, può essere pensata come un numero reale e allora diremo che il tempo varia in modo continuo, cioè senza salti (come se fosse misurato con un orologio analogico) oppure come un numero naturale, cioè t = 0, 1, 2, ... e diremo allora che il tempo varia in modo discreto, assumendo valori multipli di una data unità di misura, che potrebbe essere un'ora, un giorno o un anno, a seconda del sistema che si sta descrivendo. Nel primo caso si parla di sistemi dinamici a tempo continuo; nel secondo, a tempo discreto.
Quale delle due rappresentazioni sia più adatta a descrivere un sistema reale, dipende dalla situazione che si sta analizzando. Ad esempio, nella descrizione del moto di un pendolo o dello scorrere dei fluidi, si usano sistemi a tempo continuo mentre, nella descrizione dell'andamento temporale di una popolazione di insetti, caratterizzati da stagioni riproduttive, si usano sistemi a tempo discreto con unità di tempo pari all'intervallo che intercorre fra due generazioni successive.
Da un punto di vista formale, conoscere un sistema dinamico significa conoscere una funzione che (una volta assegnato il vettore di stato x0, ad un dato istante iniziale t0) permetta di determinare univocamente lo stato del sistema ad ogni istante di tempo successivo:
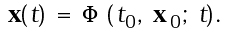
Data una condizione iniziale x0(t0), l'insieme di tutti i valori x(t), ottenuti mediante l'applicazione della funzione F, costituisce la traiettoria del sistema dinamico passante per la condizione iniziale assegnata. In pratica, conoscere le traiettorie significa poter calcolare lo stato del sistema ad un qualunque istante futuro, sulla base della conoscenza dello stato ad un certo istante. In un sistema dinamico a tempo continuo, una traiettoria può essere pensata come una curva nello spazio n-dimensionale delle fasi mentre, in un sistema dinamico a tempo discreto, una traiettoria è costituita da una successione di punti.
In realtà, non è affatto facile conoscere l'operatore F, ma si cerca di risalire ad esso attraverso la formulazione di leggi di evoluzioni locale o equazioni del moto. Nel caso di modelli a tempo continuo, le leggi del moto sono espresse mediante equazioni differenziali, che descrivono come la rapidità di variazione di ciascuna variabile di stato (espressa dalla derivata prima rispetto al tempo) dipenda da se stessa e dalle altre variabili:
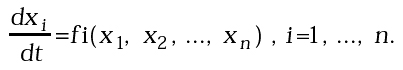
Solo nei casi più semplici si può arrivare ad ottenere la soluzione generale del problema che verifica le condizioni iniziali assegnate, ovvero la funzione F. Ad esempio, consideriamo l'equazione differenziale lineare:
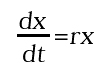
con condizione iniziale x(t0) = x0. La soluzione è:
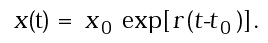
In altre parole, partendo da una legge locale, in base alla quale il tasso di variazione di una variabile è proporzionale al valore della variabile stessa, come accade ad esempio nei modelli di crescita di una popolazione (con r > 0) o di decadimento radioattivo (con r < 0), si ottiene in forma esplicita l'operatore di evoluzione temporale che prevede, rispettivamente, una crescita o un decadimento esponenziale.
Un altro esempio famoso è quello di un oscillatore armonico (ad esempio, un corpo appeso a una molla) la cui equazione del moto è espressa dalla seconda legge della dinamica, massa per accelerazione = forza, che diventa un'equazione differenziale del secondo ordine:
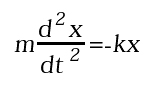
dove la variabile x rappresenta lo spostamento rispetto alla posizione di equilibrio della molla e -kx è la forza elastica di richiamo. Questo modello si presenta in una forma diversa poiché contiene la derivata seconda, ma può essere trasformato introducendo, come seconda variabile di stato, la velocità istantanea
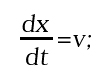
e ottenendo così un sistema di due equazioni differenziali del primo ordine:
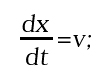
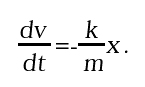
Anche in questo caso è possibile risalire all'espressione analitica della traiettoria: se assumiamo che il corpo parta da fermo, con uno spostamento iniziale x0 rispetto alla posizione di equilibrio, cioè prendiamo come condizione iniziale (x(0), v(0)) = (x0, 0), allora la soluzione è:
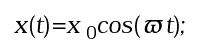
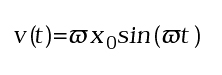
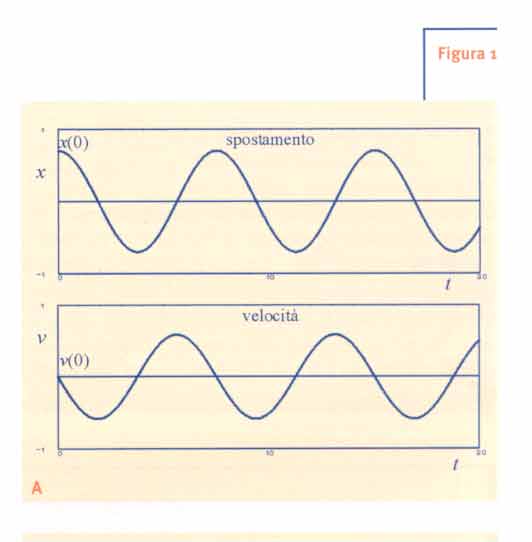
con omega-segnato che è la radice quadrata del rapporto tra k e m. Questa soluzione può essere rappresentata graficamente riportando l'andamento di ciascuna delle due variabili x(t) e v(t) in funzione del tempo (come in Fig.1A) oppure riportando, per ogni t, ivalori di x(t) e v(t) sul piano cartesiano (x,v), come in Fig.1B.
 |
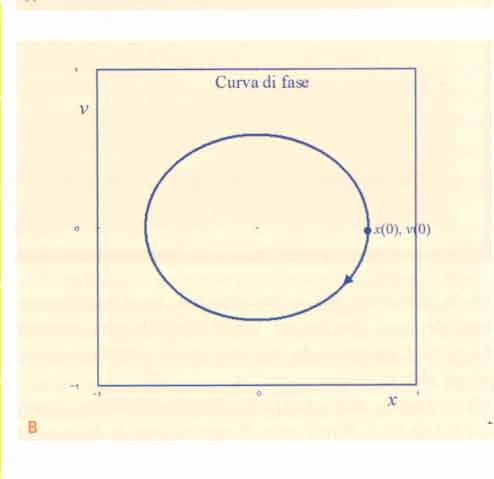 |
Quest'ultima rappresentazione è detta curva di fase o orbita.
In questi esempi, la facilità ad ottenere le soluzioni in forma analitica è legata al fatto che abbiamo ottenuto equazioni differenziali lineari, in cui cioè i secondi membri erano polinomi di primo grado nelle variabili di stato. Se si considerano modelli non lineari, come spesso accade nella descrizione dei sistemi reali, trovare una soluzione in forma analitica è in genere un'impresa difficile, spesso impossibile.
Analoghe considerazioni valgono anche per modelli dinamici a tempo discreto. In questo caso, preso come unità di misura l'intervallo temporale scelto per scandire il tempo, la legge del moto viene rappresentata sotto forma di equazioni alle differenze:
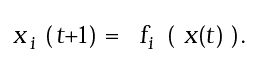
Partendo dalla condizione iniziale, l'intera traiettoria si può ottenere induttivamente: da x(0) si ottiene x(1), il quale può essere preso come nuovo argomento delle funzioni fi per ottenere x(2) e così via, come visualizzato in Fig.2.

Ovviamente, questo procedimento iterativo si basa sull'ipotesi che ciascuna funzione fi abbia come dominio l'insieme M degli stati possibili e che anche i codomini delle fi non escano dallo spazio degli stati, in modo che sia possibile applicare di nuovo le funzioni fi alle variabili di stato. L'esempio più semplice è l'iterazione di una funzione (o mappa) lineare:
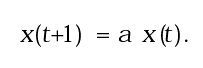
Partendo dalla condizione iniziale x(0), si ottiene:
x(1) = a x(0) ; x(2) = a x(1) = a2 x(0); ...
x(t) = a x(t-1) = a ( a t-1 ) x(0)= a t x(0).
Dalla conoscenza esplicita della successione x(t)= a t x(0), detta progressione geometrica di ragione a, è possibile il calcolo diretto dello stato dopo n intervalli temporali in base alla conoscenza dello stato iniziale. Inoltre, si deduce in modo immediato il comportamento asintotico, per t che tende ad infinito, della traiettoria: per |a|<1, x(t) converge a 0; per |a|>1, x(t) diverge. Inoltre, se è a < 0, l'andamento è di tipo oscillatorio; mentre se a > 0, si ha una successione monotòna.
Ma la situazione non è così semplice, se si considerano leggi del moto non lineari. Infatti, iterando una generica funzione f partendo da una condizione iniziale (o punto seme) x(0), si ottiene:
x(1) = f (x(0)); x(2) = f (x(1)) = f(f(x(0))) = f2 (x(0)); ... ,
x(t) = f (f (x(t-1)) = ft(x(t)) dove ft rappresenta la funzione f composta con se stessa t volte, espressione che in generale sarà estremamente ingombrante e in pratica impossibile da scrivere. Non è facile, quindi, capire il comportamento asintotico delle traiettorie, cioè quale sarà il loro destino al crescere di t.
Con queste premesse formali, siamo ora in grado di dare la seguente definizione: la teoria dei sistemi dinamici è l'insieme dei metodi matematici attraverso i quali si cerca di ottenere, in maniera più o meno esplicita, informazioni sull'operatore di evoluzione temporale F partendo da una sua rappresentazione locale (o legge del moto) assegnata in forma di equazioni differenziali o alle differenze.
Non si tratta di un settore della Matematica particolarmente recente. La sua nascita può essere fatta risalire a Newton, il quale (in una lettera inviata a Leibnitz nel 1677) scrisse che aveva trovato un metodo di lavoro importante, che non poteva rivelare in modo palese. Infatti, lo fece proponendogli un anagramma, in una forma quasi impossibile da decifrare. La frase decodificata, diventata famosa con il nome di anagramma fondamentale del Calcolo, è la seguente:"Data aequatione quotcunque fluentes quantitae involvente fluxiones invenire et vice versa", che significa: "Data un'equazione che contiene un numero qualunque di quantità fluenti [oggi, diremmo derivate] trovare le flussioni [oggi, diremmo le primitive] e viceversa".
Ovviamente, il metodo divenne poi patrimonio comune e strumento privilegiato per lo studio dei sistemi naturali che evolvono nel tempo, tanto che Pierre Simon de Laplace, nel 1776, ipotizzava l'esistenza di un sistema dinamico in grado di regolare, in modo rigidamente deterministico e prevedibile, l'intero Universo: "lo stato attuale del sistema della natura consegue evidentemente da quello che era all'istante precedente e se noi immaginassimo un'intelligenza che a un istante dato comprendesse tutte le relazioni fra le entità di questo universo, essa potrebbe conoscere le rispettive posizioni, i moti e le disposizioni generali di tutte quelle entità in qualunque istante del futuro".
Laplace sapeva bene che la conoscenza delle diverse entità (quelle che ora chiamiamo variabili di stato) ad un certo istante non può essere ottenuta con infinita precisione, essendo il frutto di processi di misura. Ma, come spesso si assume in base a regole di buon senso, considerava ovvio il fatto che una piccola incertezza nei valori delle condizioni iniziali avesse conseguenze altrettanto piccole sull'intera traiettoria e che quindi il calcolo dello stato futuro risultasse di poco alterato. In altre parole, il fatto di poter rappresentare l'evoluzione di un sistema reale mediante un sistema dinamico, sia pur attraverso una sua rappresentazione locale, era considerato equivalente a dire che la sua evoluzione fosse necessariamente regolare, prevedibile, priva di ogni incertezza.
Eppure, qualche piccolo indizio che le cose non stessero proprio così era già presente in quei settori in cui le equazioni del moto erano non lineari. Ad esempio, nella dinamica dei fluidi, si potevano osservare sia andamenti regolari che complessi. Il fumo di una sigaretta, o il flusso dell'acqua nell'alveo di un fiume, possono talvolta evolvere in modo semplice (il cosiddetto moto laminare) e altre volte in modo vorticoso e disordinato (il cosiddetto moto turbolento) pur essendo governati dalle stesse equazioni del moto. Il passaggio alla turbolenza, che si osserva talvolta in modo improvviso durante il moto di liquidi o gas, è stato uno dei problemi che maggiormente hanno stimolato gli studi sui sistemi dinamici non lineari. Si racconta che Heisenberg, uno dei padri della Fisica quantistica e premio Nobel per la Fisica nel 1932, pochi minuti prima di morire abbia detto: "quando nell'aldilà avrò l'opportunità di interrogare il Creatore, gli voglio chiedere due cose: perché la relatività e perché la turbolenza. Almeno sulla prima spero di ottenere una risposta".
In effetti, agli inizi del XX secolo l'interesse per questo settore sembrava destinato a ridursi, per mancanza di argomenti nuovi da proporre. C'erano problemi non risolti, come la turbolenza dei fluidi, ma la loro soluzione appariva così difficile elontana che sembrava non valesse la pena dedicarvi ulteriori sforzi.
I motivi per il risveglio di interesse vennero dagli studi del matematico, fisico e filosofo francese Henri Poincaré (1854-1912) che può essere considerato il fondatore della teoria qualitativa (o topologica) dei sistemi dinamici ovvero di un modo di studiare le leggi del moto che rinuncia a ogni pretesa di conoscenza analitica o numerica delle soluzioni e si basa su metodi di tipo geometrico-visivo. Partendo da un problema apparentemente semplice, il moto di tre corpi che interagiscono tra loro attraverso la forza di gravità, Poincaré arrivò a descrivere in modo chiaro il fenomeno del caos deterministico, scrivendo nel 1903: "una causa piccolissima che sfugga alla nostra attenzione determina un effetto considerevole che non possiamo mancare di vedere, e allora diciamo che l'effetto è dovuto al caso. Se conoscessimo esattamente le leggi della natura e la situazione dell'universo all'istante iniziale, potremmo prevedere esattamente la situazione dello stesso universo in un istante successivo. Ma se pure accadesse che le leggi naturali non avessero più alcun segreto per noi, anche in tal caso potremmo conoscere la situazione iniziale solo approssimativamente. Se questo ci permettesse di prevedere la situazione successiva con la stessa approssimazione, non ci occorrerebbe di più e dovremmo dire che il fenomeno è stato previsto. Ma non è sempre così; può accadere chepiccole differenze nelle condizioni iniziali ne producano di grandissime nei fenomeni finali. Un piccolo errore nelle prime produce un errore enorme nei secondi. La previsione diviene impossibile".
In effetti, la visione di Laplace (oltre che nei sistemi lineari) è corretta anche nei sistemi non lineari, purché lontani dai regimi di comportamento caotico. Ma in modelli non lineari, anche semplici, le traiettorie possono risultare molto simili a successioni di stati aleatori, cioè ottenuti con l'intervento di elementi casuali (come le uscite nel lancio di un dado).
I risultati ottenuti da Poincaré erano probabilmente troppo avanzati rispetto ai suoi tempi e non suscitarono subito l'interesse che meritavano. Ma la rivoluzione scientifica provocata dalla scoperta del caos deterministico era solo ritardata. Dopo ulteriori importanti contributi alla teoria qualitativa dei sistemi dinamici, forniti dalla grande scuola russa dagli anni '30, con Lyapunov, Kolmogorov, Andronov, Pontrjaguine e dagli studi di Birkhoff negli Stati Uniti, due articoli diedero un decisivo contributo alla diffusione e alla crescente popolarità di questo settore della Matematica: quello del 1963 del meteorologo americano Edward Lorenz e quello del 1976, dal titolo Semplici modelli matematici con dinamiche molto complicate, in cui Robert May - un fisico inglese che studia modelli per l'Ecologia - illustrò con un linguaggio accessibile anche a non specialisti l'insorgere di dinamiche caotiche attraverso lo studio di un sistema dinamico a tempo discreto, ottenuto iterando un polinomio di secondo grado (una "banale" parabola).
Seguiamo anche noi la strada indicata da May, analizzando il seguente modello dinamico a tempo discreto:
x (t+1) = f (x(t))= (1 - r - sx(t)) x(t) - h.
Questa equazione alle differenze ci permette di introdurre alcuni importanti concetti che caratterizzano anche i sistemi dinamici non lineari a tempo continuo. Essa costituisce anche un modello per descrivere l'andamento temporale di una popolazione di densità x dove il parametro r rappresenta il tasso di crescita nell'unità di tempo, il termine -sx rappresenta un termine di mortalità dovuta a sovraffollamento (competizione per il cibo o per lo spazio vitale) e -h il tasso di prelievo (ad esempio, se parliamo di popolazioni ittiche, un'attività di pesca a quote fisse).
Il primo passo per affrontare lo studio qualitativo di un sistema dinamico consiste nell'identificarne i punti di equilibrio (o stati stazionari) definiti come quei valori della variabile di stato che rimangono costanti sotto l'azione della legge del moto: x(t+1) = x(t). Si tratta quindi dei punti fissi della funzione f, soluzioni dell'equazione f(x)=x, rappresentati graficamente dalle intersezioni del grafico della funzione y = f(x) con la retta bisettrice di equazione y = x. Nel caso del nostro modello, è f (x) = -sx2 + (1-r) x -h e quindi l'equazione f(x) =x dà sx2 + rx + h = O. Per h < r2/(4s) si ottengono allora due punti fissi:
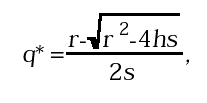
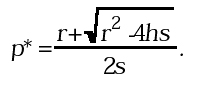
Se la condizione iniziale viene presa in corrispondenza di un punto fisso x*, la traiettoria che si ottiene è stazionaria, cioè x(t) = x* per ogni t.
È allora naturale chiedersi cosa succede se, anziché partire esattamente da x*, si parte da una condizione iniziale x(0) vicina a x*. Per analizzare questo problema, ricorriamo a una comoda costruzione grafica per studiare le traiettorie ottenute dall'iterazione di una funzione di una sola variabile.
Consideriamo il grafico della funzione y = f (x), che nel nostro esempio è una parabola concava, e sovrapponiamo ad esso il grafico della bisettrice y = x. Partendo dalla condizione iniziale x(0), presa sull'asse delle ascisse, tracciamo un segmento verticale fino a incontrare il grafico della funzione e poi procediamo in orizzontale fino all'asse y per ottenere x (1) = f (x(0)). Per procedere nell'iterazione, occorre ora riportare x(1) sull'asse delle ascisse, in quanto dovrà diventare il nuovo argomento su cui applicare la funzione per ottenere x(2). Questo può essere ottenuto sfruttando la presenza della bisettrice che, essendo il luogo di equazione y = x, permette di riportare x(1) sull'asse orizzontale mediante uno spostamento orizzontale verso destra e uno verticale verso il basso, usando la bisettrice come punto di svolta. Ora siamo pronti a ripetere lo stesso procedimento per ottenere x(2) = f (x(1)) e così via. Si può notare l'inutilità del segmento che congiunge il grafico della funzione con l'asse delle y (che viene subito ripercorso all'indietro verso la bisettrice) e lo stesso ragionamento si puòapplicare al segmento verticale: per non percorrerlo due volte, prima in discesa e poi in salita, è conveniente fermarsi sulla bisettrice e da qui subito dirigersi verso il grafico per determinare l'iterato successivo. In tal modo, la sequenza di passi da un iterato al successivo diventa: x(t) (sulla bisettrice) -> tratto verticale ->grafico della funzione -> tratto orizzontale -> x(t+1) (sulla bisettrice) come visualizzato in Fig. 3. Si viene così a sostituire l'asse x con la bisettrice ed è su essa che si rappresenta la sequenza {x(0),
x(1), ..., x(t), ...}.
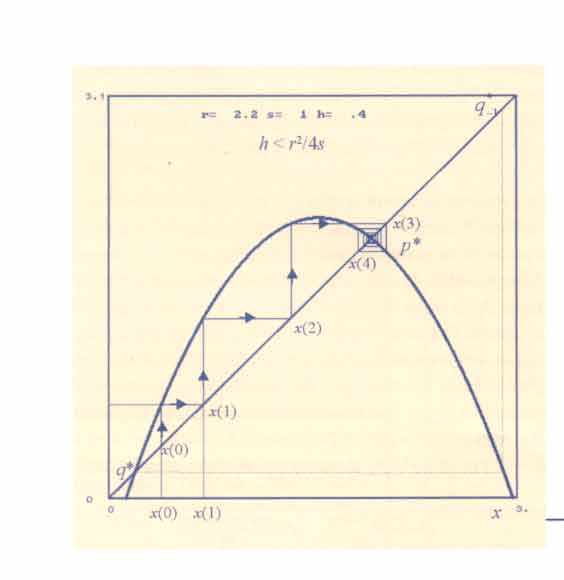
Figura 3
Dalla Fig. 3 (ottenuta con parametri r = 1.5, s = 1, h = 0.2) ci rendiamo conto che i due equilibri si comportano diversamente. Partendo da una condizione iniziale in un intorno di q*, la traiettoria si allontana da esso (e non vi ritorna più); partendo da una condizione iniziale vicina a p*, la traiettoria generata si avvicina invece asintoticamente ad esso cioè converge a p*. Si dice allora che q* è un equilibrio instabile (o repulsivo) mentre p* è asintoticamente stabile (o attrattivo).
La differenza fra i due equilibri si può giustificare osservando la pendenza con cui il grafico della funzione attraversa la bisettrice in corrispondenza dei punti fissi: in q* la pendenza è superiore a quella della bisettrice, cioè il coefficiente angolare f ´(q*) della retta tangente al grafico, x(t+1) = q*+ f ´(q*) (x(t)-q*), è maggiore di 1. Quindi la funzione iterata si comporta, in un intorno del punto fisso, come una mappa lineare di ragione maggiore di 1 (una progressione geometrica espansiva). Applicando lo stesso ragionamento all'equilibrio p*, possiamo invece dire che l'approssimazione lineare della funzione in un suo intorno si comporta come una progressione geometrica contrattiva, essendo il coefficiente angolare della tangente minore di 1 in valore assoluto. Inoltre, la convergenza è di tipo oscillatorio (con oscillazioni smorzate) in quanto il coefficiente angolare in p* è negativo.
La stabilità è un concetto locale, poiché viene definita in base al comportamento delle traiettorie che partono da condizioni iniziali prese vicino all'equilibrio. La domanda che sorge spontanea - quanto vicine? - porta al concetto di bacino di attrazione, definito come l'insieme dei punti che generano traiettorie convergenti a un dato attrattore. Nel nostro caso, il bacino è delimitato dal punto fisso instabile e dalla sua pre-immagine, indicata con q*-1 in Fig. 3 (pre-immagine di q* significa che f (q*-1) = q*). Nella situazione di Fig. 3, si hanno quindi due tipi di dinamiche asintotiche: se x(0)‘ (q*,q*-1), allora la traiettoria che parte da x(0) converge all'equilibrio p*; per x(0) < q* oppure x(0) > q*-1, la traiettoria diverge invece a -infinito (per l'applicazione considerata, questo equivale all'estinzione della popolazione).
Entrambi i valori di equilibrio dipendono dal parametro h e al crescere di h si avvicinano tra loro: p* diminuisce e q* aumenta (aumentando la quota prelevata nell'unità di tempo, il valore di equilibrio stabile diminuisce e il valore di soglia, sotto il quale la specie andrà all'estinzione, aumenta ovvero il sistema diventa più vulnerabile).
Quando il parametro h raggiunge il valore h = r2/4s, i due punti di equilibrio si sovrappongono e la parabola diventa in tali punti tangente alla bisettrice (Fig. 4A). Un ulteriore aumento di h provoca la scomparsa dei due equilibri, dopodiché l'unica evoluzione possibile è quella che conduce all'estinzione (Fig. 4B).
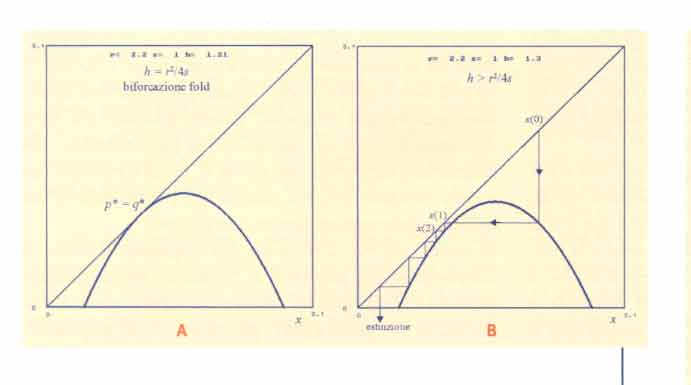
Figura 4
Il valore h = r2/4s è un valore di biforcazione, che prende il nome di biforcazione tangente (o biforcazione fold). In generale, si dice che un parametro attraversa un valore di biforcazione quando determina il passaggio fra due situazioni dinamiche qualitativamente diverse, dovuto ad esempio alla creazione o scomparsa di punti fissi o altri tipi di attrattori, oppure cambiamenti di stabilità.
Nell'esempio proposto, le biforcazioni che portano al caos si verificano agendo sui parametri in modo da rendere più acuminata la parabola. Per mostrare ciò, fissiamo h = 0 (popolazione non sfruttata) e facciamo aumentare il parametro r, usandolo come una "manopola" per innalzare il vertice. Per h=0, i punti fissi diventano q*=0 e p*= r/s (valore di equilibrio della popolazione non sfruttata). Al crescere di r, il grafico della funzione in corrispondenza del punto fisso p* diventa via via più ripido, fino a che la pendenza raggiunge il valore -1, cioè la tangente diventa perpendicolare alla bisettrice. Questo accade per r = 2, poiché il coefficiente della retta tangente al grafico in p* è f ´(p*) = 1+r - 2sp*= 1-r. Un aumento ulteriore di r provoca quindi una perdita di stabilità dell'equilibrio positivo; r = 2 costituisce pertanto un valore di biforcazione. Per cercare di capire il tipo di biforcazione, esaminiamo il comportamento dinamico delle traiettorie per valori di r poco maggiori di 2 e con condizione iniziale prossima a p*. Quello che si può vedere è che la traiettoria si allontana da p*, oscillando, e tende a un'oscillazione periodica fra due punti (indicati con alfa e beta in Fig. 5A).
 | Partendo da uno di questi due punti, si ottiene una traiettoria che saltella tra alfa e beta, essendo f(alfa) = beta e f(beta) = alfa. Inoltre, allo stesso ciclo-2 tende ogni traiettoria che parte da una condizione iniziale x(0)‘ (q*,q*-1) = (0, (1+r)/s), esclusa x(0) = p* naturalmente. Questo tipo di biforcazione si chiama biforcazione con raddoppio del periodo o, più brevemente, biforcazione flip. Per capire meglio quello che accade, consideriamo la funzione composta F(x) = f (f (x))= f 2(x), il cui grafico è mostrato in Fig. 5B. Poiché F(x) è un polinomio di quarto grado, può avere fino a 4 intersezioni con la bisettrice, ossia quattro punti fissi. Due sono necessariamente gli stessi di f, ossia q* e p*, mentre eventuali altri corrispondono ai punti periodici (di periodo 2) di f essendo F(alfa) = f (f (alfa)) = f(beta) =alfa e, analogamente, F(beta)=beta. In effetti, iterare la mappa F significa generare gli stati del sistema a salti di 2. Figura 5 |
La biforcazione che avviene nella mappa f per r=2 corrisponde a ua perdita di stabilità di p* anche per l'iterata: è F ´(p*)=[f ´(p*)]2 e quindi abbiamo F ´(p*) „ 1 per r „ 2. Aumentando ulteriormente il parametro r, anche la pendenza di F nei suoi punti fissi alfa e beta raggiunge il valore -1 e quindi avviene una biforcazione flip che fa diventare alfa e beta instabili per F, mentre attorno a ciascuno di loro si crea un ciclo di F di periodo 2. Tali cicli-2 stabili rappresentano un ciclo-4 stabile per f, che diventa l'attrattore "di turno" del sistema dinamico, e contemporaneamente costituiscono 4 punti fissi stabili per f4. Aumentando ancora r, tale ciclo-4 diventerà instabile lasciando il posto a un ciclo-8 così via. È naturale chiedersi cosa avverrà nel seguito: si raggiungerà un ciclo di periodo massimo (dopo il quale, le biforcazioni con raddoppio del periodo finiranno) o i raddoppi continueranno all'infinito?
Per analizzare ciò, si ricorre alla costruzione di un diagramma di biforcazione. Si considera un piano cartesiano in cui si riportano sull'asse orizzontale i valori del parametro r preso in un certo intervallo, ad esempio r appartente all'intervallo [1,3] e per ogni valore del parametro si calcolano i primi N punti della traiettoria, dove N è un numero sufficientemente grande (ad esempio N = 500). Sulla verticale passante per il valore di r utilizzato, si riportano i valori "asintotici" della x, cioè i valori più avanzati fra quelli calcolati, ad esempio i valori
{x201, ...,x500}. Infatti, una volta eliminato il transitorio {x0, ...,x200}, i valori rappresentati si troveranno sull'attrattore "di turno" e quindi la loro posizione può essere considerata come una rappresentazione dell'attrattore per il valore del parametro considerato.
In Fig. 6 (seguendo il diagramma di biforcazione) possiamo osservare che, al crescere di r, si hanno successivi raddoppi di periodo: da 4 a 8, poi a 16, 32, ... e tutta la successione delle potenze di 2.
Inoltre è importante osservare che i valori di r, per i quali avvengono le biforcazioni di raddoppio del periodo, da 2k a 2k+1, sono sempre più vicini fra loro al crescere di k. Infatti, la variazione di r necessaria per passare dalla creazione del ciclo-2 (che avviene per r = r1= 2) alla creazione del ciclo-4, che avviene per r = r2= EF6, è di (Delta(r))1=
(r2- r1) (circa) = 0.449 , mentre la variazione di r che intercorre fra la creazione del ciclo-4 e del ciclo-8 è (Delta(r))2=(r3 - r2) (circa) =
(3.544-3.449) = 0.095. I raddoppi di periodo diventano sempre più frequenti, ovvero gli intervalli (Delta(r))k diventano sempre più piccoli. Ciò si può osservare nel diagramma di biforcazione di Fig. 6, in cui è evidente che il ciclo attrattivo di turno rimane tale per un intervallino dell'asse delle ascisse sempre più piccolo.
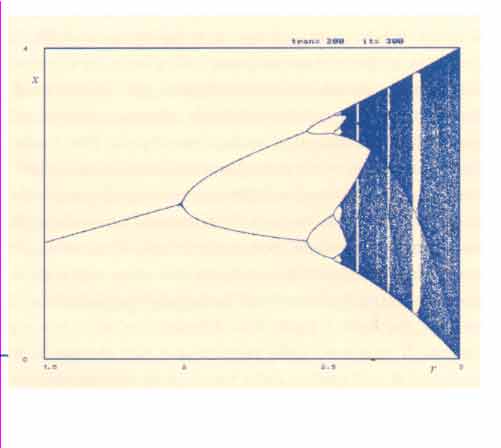
Figura 6
In realtà, per r > 2.56 si ha una sequenza di valori di biforcazione così numerosi e ravvicinati da far pensare appunto ad una cascata. La cosa più sorprendente è che, per valori di r vicini a 2.57, gli infiniti cicli di periodo 2k, k appartenente ad N, sono stati tutti creati. In altre parole, la sequenza di valori di biforcazione {r1, r2, ..., rn, ...} ha un punto di accumulazione, noto come numero di Feigenbaum, e dato da rinfinito=2.56994...
Dopo questo valore di r compaiono delle traiettorie che non sono periodiche. Sono cioè costituite da valori che non coincidono mai con un valore già ottenuto, caratterizzate dal fatto che i punti riempiono densamente uno o più intervalli. Infatti, nel diagramma di biforcazione cominciano a comparire, lungo la verticale, delle zone nere (densamente riempite di punti). Se prendiamo una di tali traiettorie e la rappresentiamo lungo l'asse dei tempi, otteniamo sequenze di punti come quelle mostrate in Fig. 7A, ottenuta per r = 2.678. Da questi andamenti, si intuisce l'origine del termine caos deterministico: sebbene i valori delle x(t) siano ottenuti attraverso l'applicazione ripetuta della funzione f - un meccanismo puramente deterministico - questi sembrano susseguirsi in modo apparentemente casuale, senza alcuna regolarità o ricorrenza.
Una delle cause di un comportamento così disordinato è da ricercarsi nel fatto che, intrappolati all'interno dell'intervallo in cui si muovono le traiettorie caotiche, ci sono infiniti punti periodici repulsivi. Essendo le traiettorie limitate, poiché i valori ottenuti iterando la mappa non possono uscire dall'intervallo I = (0, r/4), e non convergendo ad alcun ciclo attrattivo, esse "rimbalzano" continuamente, respinte dai punti periodici repulsivi che sono sparsi (e densi) all'interno dell'intervallo I.
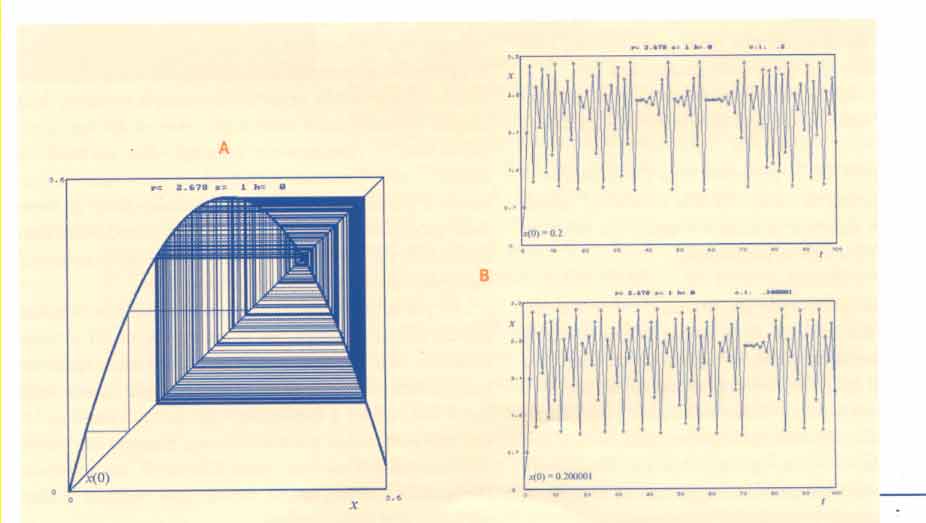
Figura 7
Un altro fatto importante, e per molti aspetti stupefacente, caratterizza le traiettorie caotiche: la difficoltà di ottenerne due identiche. In linea di principio, data la stessa mappa e data la stessa condizione iniziale, le traiettorie dovrebbero essere identiche. Ma quando le traiettorie sono caotiche, basta una minima differenza fra due condizioni iniziali per ottenere traiettorie completamente diverse. E minime differenze possono anche essere introdotte a causa della precisione limitata con cui vengono rappresentati i numeri ovvero dal numero delle cifre usate per fare i calcoli.
Questo fatto è illustrato in Fig. 7B, dove la prima traiettoria è stata ottenuta partendo da una certa condizione iniziale mentre la seconda è stata ottenuta con una condizione iniziale, che differisce di pochissimo, solo un milionesimo ovvero 10-6 = 0.000001. Ebbene, dopo alcune iterazioni in cui si ottengono valori simili, le due traiettorie cominciano a differenziarsi sempre di più, fino a diventare completamente diverse. Il fatto che una piccola variazione nelle condizioni iniziali (anche quasi impercettibile o difficilmente misurabile) abbia conseguenze così notevoli nell'evoluzione di un sistema dinamico caotico è stato chiamato sensitività rispetto alle condizioni iniziali o anche effetto farfalla.
Cos'è quindi il caos deterministico? In realtà, una sua definizione generale, applicabile a tutti i casi in cui tale fenomeno si manifesta, non esiste ancora. Si riconosce la presenza del caos in tutti i casi in cui si ottengono traiettorie limitate che soddisfano le seguenti tre condizioni:
(1) Sensitività rispetto alle condizioni iniziali: partendo da due diverse condizioni iniziali, arbitrariamente vicine fra loro, la distanza fra le rispettive traiettorie cresce esponenzialmente e, dopo un numero finito di iterazioni, diventa dello stesso ordine di grandezza della variabile di stato.
(2) Transitività (o mixing): i punti della traiettoria generata, partendo da una generica condizione iniziale, ricoprono densamente una zona dello spazio delle fasi.
(3) Esistenza di infiniti cicli repulsivi, con i punti periodici densi nella regione ricoperta dalle traiettorie caotiche.
Si può dimostrare che le proprietà (2) e (3) implicano la (1), ma la proprietà di sensitività alle condizioni iniziali viene in genere riportata in quanto è quella più semplice ed evidente (ed è anche la più famosa).
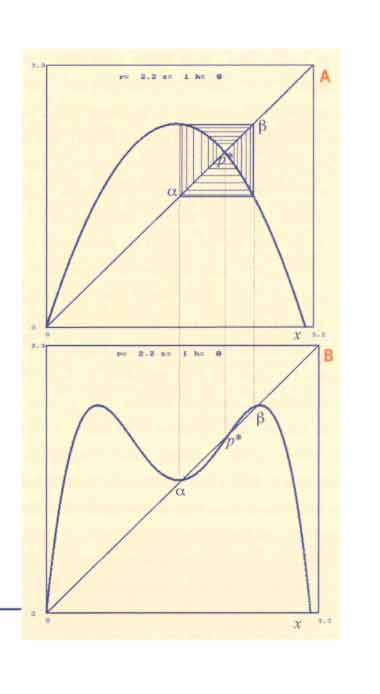
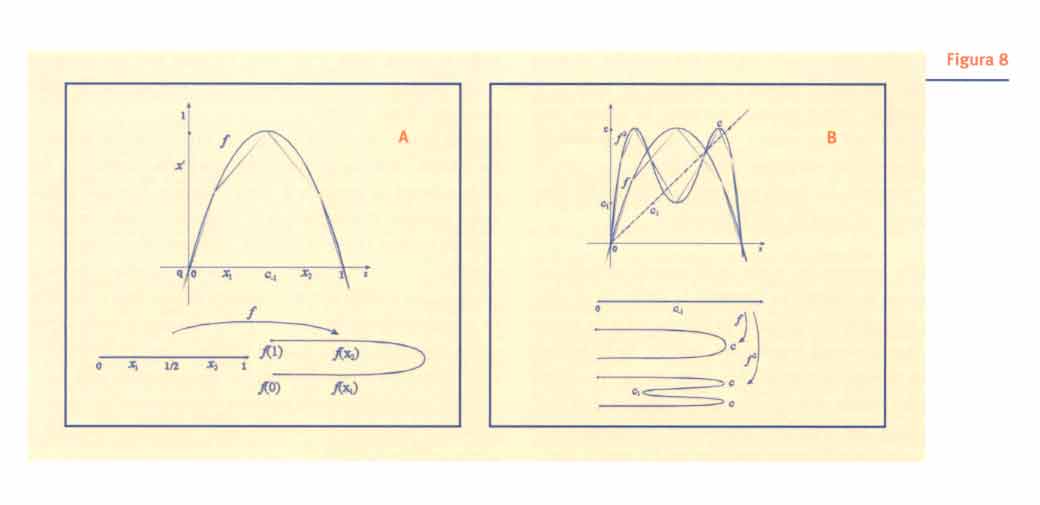
Per capire le caratteristiche geometriche, o topologiche, del caos deterministico, si deve tenere presente che la mappa considerata (la parabola) agisce su un segmento allungandolo in certe zone e comprimendolo in altre. Se il segmento include il punto critico x=1/2, lo ripiega anche (si veda Fig. 8A). Alla seconda applicazione della f, tali azioni si ripetono (si veda Fig. 8B) e così via. L'iterazione della funzione equivale quindi all'applicazione di ripetute azioni di stiramento, piegamento, compressione.
L'azione combinata di queste azioni è possibile solo con mappe non lineari, in quanto una mappa lineare o dilata o contrae (ma non entrambe le cose contemporaneamente) e non può certo causare piegamenti.
L'insorgere del caos deterministico è invece legato alle trasformazioni che provocano stiramenti e ripiegamenti. Spesso viene usata la metafora dell'azione geometrica che si esercita sull'impasto di farina e acqua quando, con il noto procedimento casalingo, si prepara la sfoglia. La principale caratteristica geometrica delle trasformazioni che generano successioni caotiche consiste in azioni combinate (e ripetute durante l'iterazione) di stiramento e ripiegamento (stretching & folding).
Il significato geometrico delle proprietà (1) e (2) risulta meglio comprensibile proprio attraverso la metafora della sfoglia. Iterando tante volte il processo di allungamento (stretching) e ripiegamento (folding), due particelle di impasto, che si trovano vicine ad un certo istante, verranno a trovarsi lontane dopo un numero finito di iterazioni (proprietà 1); un pizzico di farina inizialmente concentrato in un punto finirà con il trovarsi uniformemente distribuito su tutto l'impasto (proprietà 2).
Anche per la proprietà (3) possiamo fornire una semplice giustificazione intuitiva. Se le traiettorie di un sistema dinamico sono limitate, ovvero sono costrette a rimanere intrappolate in una regione compatta dello spazio delle fasi e tale regione è densamente ricoperta di punti periodici repulsivi, allora le traiettorie non possono che essere estremamente irregolari, come il moto di una particella che si muove in uno spazio densamente riempito di altre particelle che la respingono.


