Introduzione alle reti neurali

Introduzione

Da sempre la natura, nelle sue varie espressioni, è stata motivo di ispirazione per la Matematica offrendo forme da rappresentare, fenomeni da modellizzare e metodi da imitare. Spesso, tuttavia, la complessità o la numerosità degli elementi in gioco ha costretto i matematici a considerare ipotesi semplificative che talvolta hanno fortemente condizionato l'applicabilità dei risultati: basta pensare alla difficoltà di descrivere, mediante forme geometriche classiche, piante o fiocchi di neve o profili di montagne o nuvole.

Nel recente passato, anche sulla scia di sempre più ampie possibilità computazionali, sono state introdotte nuove idee che si fondano sullo studio di strutture la cui complessità è data dalla interazione di grandi numeri di processi ciascuno dei quali elementare.

La semplicità di fondo che sembra essere trasversale a questi diversi (e apparentemente molto lontani) ambiti trova esempi nella teoria geometrica dei frattali, negli algoritmi genetici e nelle reti neurali artificiali. Questi argomenti, nonostante siano stati introdotti recentemente, sono abbastanza noti anche ai non addetti ai lavori soprattutto per l'apparente mancanza di prerequisiti necessari a descrivere i risultati di cui trattano. A tal proposito, è interessante leggere l'articolo che Steven Krantz scrisse nel 1989 [Kra89], in cui l'autore cita i frattali come raro esempio di argomento che un matematico può proporre per illustrare la materia di cui si occupa, con qualche speranza di essere ascoltato anche dai non esperti. In realtà, la Matematica sottesa è tutt'altro che banale e risulta di grande interesse. È anche suscettibile di numerose applicazioni e la letteratura recente si arricchisce sempre più di problemi trattati con tecniche ad essa riconducibili.

L'avvio degli studi sulle reti neurali viene fatto usualmente risalire all'articolo di McCulloch e Pitts [MP43] del 1943. Seguirono, tra il 1949 ed il 1969, contributi usciti con una certa regolarità nel tempo e dovuti a Hebb [Heb49], Rosenblatt [Ros58], Widrow e Hoff [WH60] e Minsky [Min61]. Dal 1969 al 1982, si registrò una certa assenza di risultati rilevanti mentre, dal 1982 in poi, assistiamo ad un risveglio dell'interesse per l'argomento che ha condotto ad importanti contributi: Hopfield [Hop82], Minsky e Papert [MP88, Min91], Chua e Yang [YC91], Kohonen [Koh95], Rumelhart e Widrow [RWL94]. Attualmente, l'interesse per le reti neurali è molto alto e testimoniato dalle numerose pubblicazioni ad esse dedicate. Il funzionamento delle reti neurali artificiali mira a riprodurre quello delle reti neurali biologiche, costituite da un grande numero di neuroni collegati tra loro secondo varie architetture che ne determinano la funzionalità. Per comprenderne i meccanismi è allora utile considerare in maniera sommaria la struttura di un neurone biologico.

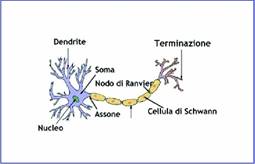
Figura 1: La struttura di un neurone

La figura 1, tratta da [Wik06b], rappresenta schematicamente un neurone; la parte centrale del neurone (dove è collocato il nucleo) si dice soma ed ha dimensioni che variano da 5µm a più di 1mm. Acquisisce informazioni dall'esterno, mediante i dendriti, ed emette un segnale che viene veicolato attraverso l'assone, un'estensione che può raggiungere una lunghezza pari a decine, centinaia o anche migliaia di volte le dimensioni del neurone (l'assone più lungo presente nel corpo umano è il nervo sciatico che parte dalla base della colonna vertebrale e termina all'alluce di ciascun piede [Wik06a]).

L'assone è rivestito di mielina che, per i neuroni periferici, è fornita dalle cellule di Schwann mentre, per i neuroni del sistema centrale, viene prodotta dagli oligodendrociti. È interrotto, a intervalli regolari, dai nodi di Ranvier che hanno importanti funzioni nella trasmissione degli impulsi e termina con una struttura che, mediante il rilascio di neuro-trasmettitori, comunica con gli altri neuroni. In funzione delle sollecitazioni cui è sottoposto, il neurone emette un segnale – si dice solitamente che si attiva – a seconda che l'input ricevuto superi o non superi un valore che si chiama soglia di attivazione. I neuroni sono interconnessi mediante collegamenti che modulano la rilevanza dei segnali trasportati. Al neurone, quindi, arriva un impulso pesato e le reti neurali sono caratterizzate, oltre che dai parametri che individuano la soglia di attivazione, anche dai pesi attribuiti ai collegamenti che li congiungono.

Le reti neurali feedforward

L'architettura delle reti neurali artificiali può essere molto varia. Spesso si trovano configurazioni organizzate su di versi strati, il primo dei quali riceve i segnali in ingresso e l'ultimo restituisce i segnali in uscita. Sono reti usualmente identificate come feedforward neural networks. Tuttavia, sono comuni anche strutture neurali in cui i segnali si propagano anche all'indietro, generando così una sorta di feedback nella rete.
A ciascuna architettura, corrisponde un diverso utilizzo. Le reti neurali feedforward (che intendiamo brevemente illustrare) ben si prestano ad essere impiegate per l'approssimazione di funzioni e per l'interpolazione.
L'estrema semplicità di un neurone artificiale rende, per certi versi, stupefacente il fatto che una rete neurale possa ben rappresentare situazioni molto complesse. Tuttavia, se contiamo il numero di variabili che entrano in gioco, anche per reti neurali costituite da un limitato numero di neuroni disposti su pochi (uno o due) strati, ci accorgiamo che si tratta di una struttura estremamente flessibile e forse pesantemente ridondante.

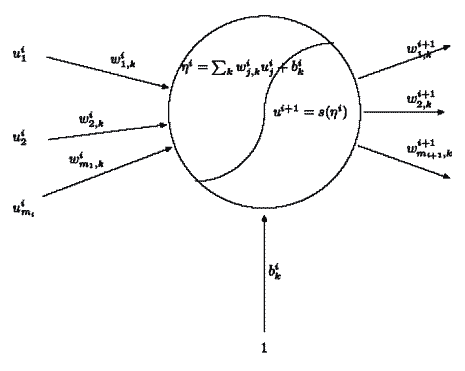
Figura 2: Il neurone artificiale

Il neurone artificiale (Figura 2) è costituito da un'unità che riceve in ingresso un valore numerico, somma pesata di diversi segnali, e lo elabora attivandosi oppure rimanendo inattivo a seconda che venga superata (o meno) la soglia di attivazione. Più specificatamente, il neurone artificiale usa il dato in ingresso come argomento per una funzione, detta appunto di attivazione, che indicheremo con la lettera s e che restituisce in uscita i valori 0, 1 – più spesso, un valore compreso in [0, 1] – e, per i neuroni dell'ultimo strato, un qualunque numero reale. Pertanto, il neurone sarà caratterizzato dalla funzione e dalla soglia di attivazione. Quest'ultima viene solitamente introdotta mediante un ingresso costante, uguale ad 1, opportunamente modulato da un coefficiente che si indica con il nome di bias, il cui effetto è quello di controllare la traslazione della soglia di attivazione rispetto all'origine dei segnali. Formalmente, il bias ha un ruolo non diverso da quello dei pesi che funzionano da regolatori dell'intensità del segnale emesso (o ricevuto).

È d'uso adottare diverse funzioni di attivazione, a seconda del ruolo che il neurone e la rete neurale sono destinati a svolgere. Sono esempi di funzioni di attivazione, frequentemente usate:

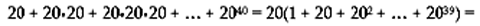
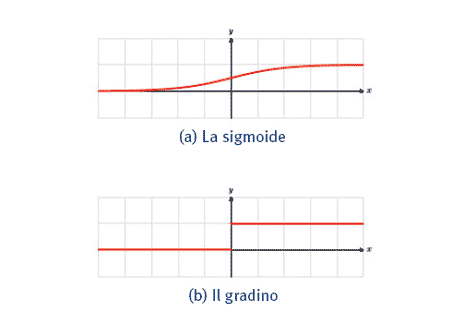
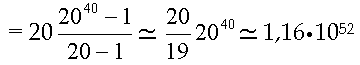
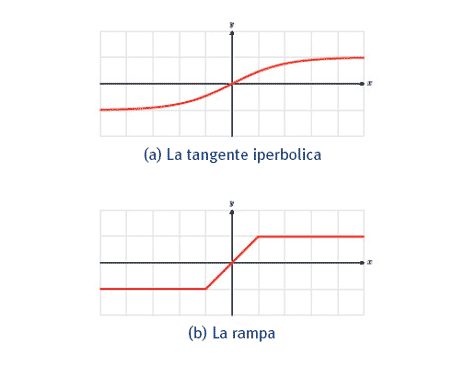
Solitamente è vantaggioso considerare, come funzione di attivazione, la sigmoide σ(x)=1/(1+e^-x) oppure la tangente iperbolica τ(x)=tanh(x), in quanto si verifica che:

σ'=σ(1-σ),
τ'(x)=1-τ²(x)=(1-τ(x))(1+τ(x))

e questo – come vedremo – semplifica in maniera significativa l'algoritmo di backpropagation mediante il quale la rete apprende dall'insieme di dati, il training set, che le vengono forniti.

Come abbiamo già detto, una rete neurale feedforward è costituita da un certo numero di strati, ciascuno formato da un certo numero di neuroni. Ogni strato riceve segnali da quello precedente, li elabora e passa il risultato allo strato successivo.
Gli strati intermedi hanno tutti le stesse caratteristiche strutturali, mentre il primo e l'ultimo sono particolari. Il primo (Figura 5) riceve segnali dall'esterno e li passa semplicemente allo strato successivo e quindi alla rete; l'ultimo (Figura 6).

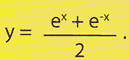
Figura 5: Un neurone del primo strato

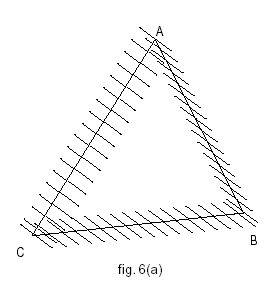
Figura 6: Un neurone dell'ultimo strato

riceve i segnali, pesati secondo i valori delle connessioni, dallo strato precedente, li somma e passa all'esterno il risultato. In altre parole, la funzione di attivazione dell'ultimo strato è semplicemente l'identità.

Ciò consente di avere in uscita un qualunque numero reale (e non soltanto un valore compreso in [0,1]) come è naturale che sia se si intende usare la rete per approssimare funzioni a valori reali.

In sostanza, un neurone che si trova nello strato i-esimo riceverà ingressi che possiamo indicare con:

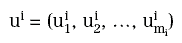
dal precedente (i – 1)-esimo strato e produrrà in uscita un segnale:

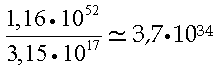
ottenuto mediante la:

dove Wⁱ= ( wⁱj,k) è la matrice dei pesi sulle connessioni e bⁱ = (bⁱk) è il vettore dei coefficienti da assegnare all'ingresso costante, uguale ad 1 (bias).

Il contributo del bias, può essere assimilato a quello degli altri ingressi. Si può tener conto del vettore di coefficienti, semplicemente aggiungendo una riga alla matrice Wⁱ:

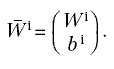
Per coerenza di notazioni, anche il vettore che definisce il comportamento della rete nei diversi strati deve essere esteso in modo da comprendere pure il contributo del bias:

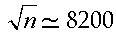
Riassumendo: una rete neurale, costituita da n strati, ciascuno dei quali composto da mi neuroni, sarà caratterizzata da n-1 matrici 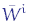  di dimensione mi-1×mi (per i=1, …, n) e da n-1 vettori riga bⁱ di dimensione mi. Possiamo allora costruire le (mi-1+1×mi)-matrici Wⁱ ed i vettori mi+1 dimensionali 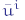prima citati in modo che, dato un segnale di ingresso:

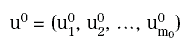
si può calcolare:

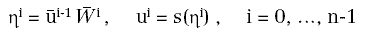
e:

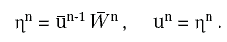
È evidente che si è così definita una funzione di tante variabili reali quanti sono i neuroni dello strato di input, a valori in uno spazio euclideo di dimensione uguale al numero di neuroni presenti nello strato di output. Come già osservato, tale funzione dipende da un gran numero di parametri e ciò la rende estremamente versatile nel modellizzare i più vari comportamenti. Potremmo dire che risulta anche troppo versatile, in quanto si possono trovare molte scelte diverse di parametri che danno lo stesso risultato.

Approssimazione di funzioni continue

Una rete neurale feedforward è in grado di approssimare ogni funzione continua. Questo teorema fu dimostrato nel 1988 da G. Cybenko [Cyb88], [Cyb89] in un ambito molto generale, ma se ne può dare anche una dimostrazione semplice e abbastanza intuitiva.

Consideriamo infatti una funzione continua f; usando il teorema di Heine-Cantor, possiamo facilmente costruire

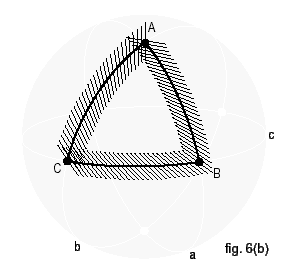
Figura 7: Approssimazione di una funzione continua mediante una funzione a scalini

una funzione a scalini che approssimi f (come mostrato in Figura 7): che può essere ottenuta come somma pesata di funzioni costanti a tratti, della forma:

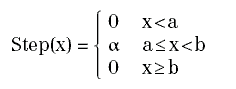
il cui grafico è del tipo rappresentato in Figura 8.

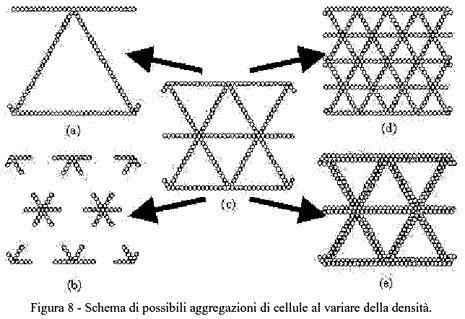
Figura 8

Le funzioni del tipo Step(·) si possono, d'altro canto, ottenere (Figura 9) come somma di due gradini:

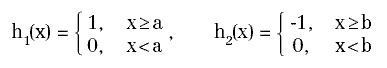
Figura 9

ciascuna delle quali rappresenta l'uscita di un singolo neurone (Figura 10).

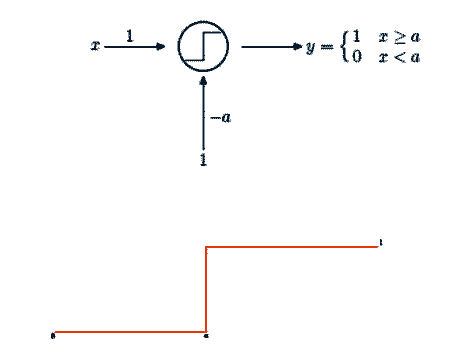
Figura 10: Il gradino come uscita del singolo neurone

Una funzione del tipo Step(·) si può quindi ottenere come output della rete neurale mostrata in Figura 11:

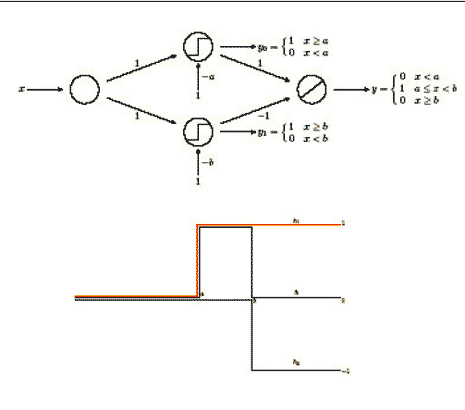
Figura 11

La rete neurale descritta nella Figura 12 definisce la funzione a scalini (il cui grafico è riportato in Figura 13) che è ottenuta come somma delle funzioni a gradino rappresentate nella Figura 14.

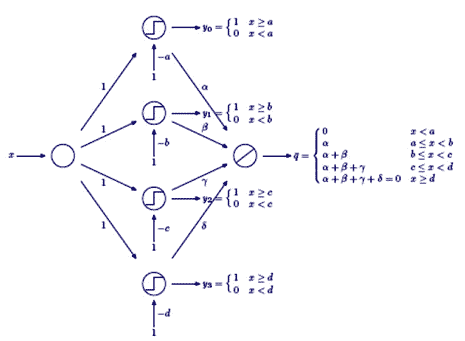
Figura 12

Figura 13

Figura 14

È quindi evidente come una rete neurale (con uno strato di input, uno di output ed un solo strato nascosto) sia sufficiente ad approssimare con qualsivoglia precisione una funzione continua, facendo uso di un numero sufficientemente grande di neuroni.

L'algoritmo di backpropagation

L'estrema flessibilità delle reti neurali le rende particolarmente adatte a svolgere compiti di approssimazione o di interpolazione. Vediamo ora come questa predisposizione possa essere utilizzata.

Siano assegnati dei dati (xj, tj)∈R^n+m (j=1,…, N) e si desideri determinare una dipendenza tra gli ingressi xj e le uscite tj. A tal fine, è ragionevole utilizzare una rete neurale. Infatti, oltre all'estrema semplicità dei componenti elementari e al gran numero di parametri disponibili, una rete neurale non richiede una scelta preventiva del tipo di funzioni da usare per la regressione.
Diventa quindi centrale il problema di determinare i coefficienti Wⁱ e bⁱ in modo che, detti oj i risultati in uscita dalla rete che corrispondono agli ingressi xj, sia minimo lo scarto quadratico tra oj e tj:

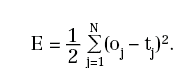
Evidentemente, E è funzione dei coefficienti della rete. Per gli scopi enunciati, occorre trovarne il minimo. Ciò può essere fatto mediante il metodo del gradiente e, nonostante l'apparente complessità dei calcoli necessari per ottenere le derivate della funzione E rispetto ad ognuno dei parametri da cui dipende, si verifica che esistono semplici formule localizzate per descriverle.

L'algoritmo, mediante il quale si aggiornano i coefficienti della rete, si definisce backpropagation in virtù del fatto che lo scarto registrato in corrispondenza di un certo dato viene fatto propagare all'indietro nella rete per ottenere le formule di aggiornamento dei coefficienti.

Per illustrare l'algoritmo di backpropagation, consideriamo il caso di una rete con uno strato di input, costituito da due neuroni, due strati nascosti (di 4 e 3 neuroni, rispettivamente) ed uno strato di output, costituito da un solo neurone. Una rete così configurata è adatta a rappresentare una funzione a valori reali (l' output dell'ultimo strato) di due varabili reali (l'input del primo strato).
La rete (rappresentata in Figura 1 5), oltre che dalla sua geometria, è identificata dalle matrici:

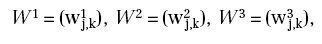
le cui dimensioni sono, rispettivamente, 2 x 4 , 4 x 3 , 3 x 1 , e dai vettori (bias):

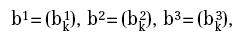
che hanno, rispettivamente, 4, 3 e 1 componenti. È inoltre utile chiamare u⁰, u¹, u², u³ i vettori che descrivono le uscite di ciascuno strato e che sono (a loro volta) di 2, 4, 3 e 1 componenti. Il vettore u⁰ avrà due componenti, che possiamo indicare con (x1, x2), per cui, se poniamo y=u³, risulterà definita una funzione reale di due variabili reali y=F(x1, x2).

I segnali in ingresso si propagano nella rete e generano un'uscita mediante le seguenti procedure:

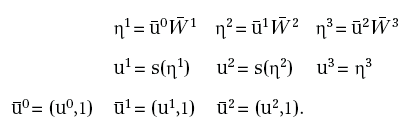
In corrispondenza di ciascun (xj, tj), per j=1, …, N, possiamo quindi porre u⁰=xj, calcolare la corrispondente uscita η³=oj e stimare l'errore:

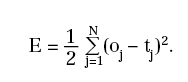
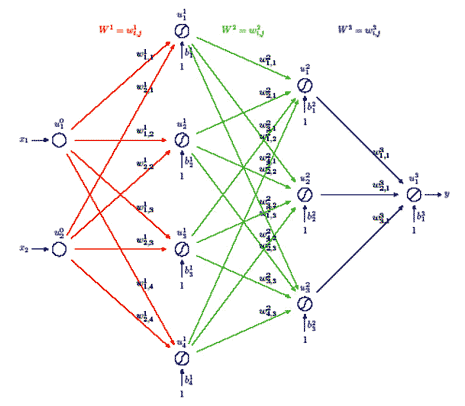
Figura 15

Se indichiamo con ζ=(W¹, W², W³), avremo E=E(ζ). Per ricavare le regole di aggiornamento della successione minimizzante, occorre calcolare:

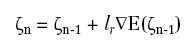
e quindi il gradiente di E. Questa operazione prende il nome di addestramento della rete neurale.

Qualora il numero N degli elementi del training set sia molto grande, pur senza maggiori complicazioni concettuali, si riscontra un appesantimento dei calcoli necessari per determinare il gradiente di E per cui, spesso, si provvede ad aggiornare le variabili considerando lo scarto quadratico calcolato su un singolo punto di riferimento (x j, tj) scelto casualmente. Minimizzare l'errore globale ottenuto sommando gli scarti quadratici su ogni punto del training set si identifica dicendo che si procede ad un aggiornamento off-line dei coefficienti; quando, invece, si considera ripetutamente l'errore ottenuto da un solo scarto quadratico, si dice che l'aggiornamento viene fatto on-line. In questo caso, spesso preferito nelle applicazioni, i punti del training set vengono proposti più volte alla rete neurale nel corso del suo apprendimento.

Risulta quindi necessario calcolare:

Usando la regola di derivazione delle funzioni composte, otteniamo:

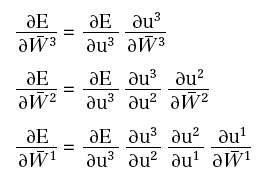
ed è facile vedere che:

e che:

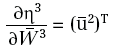
in quanto: η³=u²W³ è funzione lineare di W³. Per calcolare le altre derivate, posto:

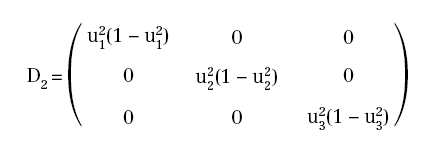
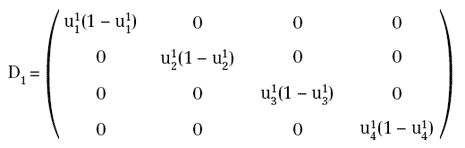
si ha:

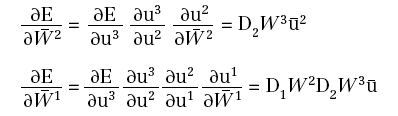
Infine, ([Roj96]), se:

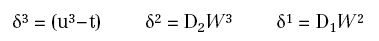
possiamo scrivere gli aggiornamenti dettati dal metodo del gradiente nella seguente maniera:

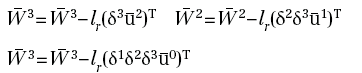
dove lr è il passo con cui il metodo del gradiente avanza ed è, in questo ambito, chiamato coefficiente di apprendimento: learning rate.

Definita la funzione errore E e calcolate le sue derivate parziali, non resta che applicare la formula di aggiornamento dei coefficienti. Ciò si presta ad essere facilmente implementato mediante un linguaggio in grado di gestire con agilità le notazioni matriciali, come Matlab. Le figure 16 e 17 sono un esempio di quanto si può ottenere.

Figura 16: Approssimazione di un piano mediante rete neurale

In Figura 16, in particolare, sono rappresentate le approssimazioni di un piano mediante una rete neurale con due strati nascosti di tre neuroni ciascuno; le prime tre immagini mostrano le approssimazioni ottenute dopo 100, 10000 e 40000 cicli di apprendimento, mentre l'ultimo grafico rappresenta l'andamento dell'errore in funzione dei cicli di apprendimento.

Figura 17:Approssimazione di una sella mediante rete neurale

La Figura 17, invece, si riferisce ad una sella ed in questo caso i primi tre grafici mostrano il risultato dell'approssimazione dopo 100, 500000 e 1000000 di cicli di apprendimento. In entrambi i casi, l'errore di approssimazione decresce solo dopo un gran numero di iterazioni e, ad un certo punto, si verifica una sua brusca diminuzione. Ciò ricorda, per certi versi, il comportamento dell'apprendimento umano.

Bibliografia

[Bis96] Cristopher M. Bishop. Neural Networks for Pattern Recognition. Clarendon Press, Oxford, 1996.

[CB90] Maureen Caudill and Charles Butler. Naturally intelligent systems. MIT Press, Cambridge, MA, USA, 1990.

[Cyb88] George Cybenko. Approximation by superpositions of a sigmoidal function. Technical report, Department of computer Science, Tufts University, Medford, MA, October 1988.

[Cyb89] G. Cybenko. Approximation by superpositions of a sigmoidal function. J-math-ctrl-sig-sys (2: 303–314, 1989).

[FS92] James A. Freeman and David M. Skapura. Neural Networks Algorithms, Applications, and Programming Techniques. Addison-Wesley, Massachusetts , 1992.

[Gur06] Kevin Gurney. Computers and symbols versus Nets and Neurons. An Introduction to Neural Networks. UCL Press, London, 2006.

[Heb49] Donald O. Hebb. The Organization of Behavior. Wiley, New York, USA, 1949.

[Hop82] John J. Hopfield. Neural networks and physical systems with emergent collective computational abilities. Proceedings of the National Academy of Sciences, 79(8): 2554–2558, April 1982.

[Kha90] Tarun Khanna. Foundations of neural networks. Addison-Wesley Longman Publishing Co., Inc., Boston, MA, USA, 1990.

[Koh95] Teuvo Kohonen. Self organizing maps. Springer, 2 edition, 1995.

[Kra89] Steven G. Krantz. Fractal geometry. Mathematical Intelligencer, 11:12–16, 1989.

[Min61] Marvin Minsky. A selective descriptor-indexed bibliography to the literature on artificial intelligence. IRE Transactions on Human Factors in Electronics, 2:39–55, 1961. Reprint: Feigenbaum & Feldman, Computers and Thought, 1963.

[Min91] Marvin Minsky. Logical versus analogical or symbolic versus connectionist or neat versus scruffy. AI Magazine, 12(2):52–69, 1991. Reprint: Luger, Computation and Intelligence, 1995.

[MP43] Warren S. McCulloch and Walter Pitts. A logical calculus of the ideas immanent in nervous activity. Bulletin of Mathematical Biophysics, 5:115–133, 1943.

[MP88] Marvin Minsky and Seymour Papert. Perceptrons. MIT Press, 2 edition, 1988.

[Roj96] Raul Rojas. Neural Networks - A Systematic Introduction. Springer-Verlag , Berlin , New-York, 1996.

[Ros58] Frank Rosenblatt. Fractal geometry. The Perceptron: A Probabilistic Model for Information Storage and Organization in the Brain, 65:386–408, 1958.

[RWL94] D.E. Rumelhart, Bernard Widrow, and M.A. Lehr. The basic ideas in neural networks. Commun. ACM, 1989). 37(3):87–92, 1994.

[Sie99] Hava T. Siegelman. Neural Networks and Analog Computation (Progress in Theoretical Computer Science). Birkhauser, Boston , Mass., 1999.

[SVM97] Johan A. K. Suykens, Joos P. L. Vandewalle, and Bart L. R. De Moor. Artificial Neural Networks for Modelling and control Systems. Kluwer Academic Publishers, Dordrecht The Nederlands, 1997.

[WH60] Bernard Widrow and Marcian E. Hoff . Adaptive switching circuits. pages 96–104. IRE, IRE WESCON Convention Record, New York, 1960.

[Wik06a] Wikipedia. Axon — wikipedia, the free encyclopedia, 2006. [Online; accessed 2-November-2006].

[Wik06b] Wikipedia. Neural network — wikipedia, the free encyclopedia.
http://en.wikipedia.org/w/index.php?title=
Neural_network&oldid=83364796, 2006. [Online; accessed 24-October-2006].

[Wik06c] Wikipedia. Neuron — wikipedia, the free encyclopedia. http://en.wikipedia.org/w/index.php?title=Neuron&oldid= 83070568, 2006. [Online; accessed 24-October-2006].

[YC91] L. Yang and Leon O. Chua. Cellular neural network a/d conversion. Technical Report UCB/ERL M91 /20, EECS Depa rt ment, Universi ty of California, Berkeley, 1991.

[ZDL90] Steven F. Zornetzer, Joel L. Davis, and Clifford Lau, editors. An introduction to neural and electronic networks. Academic Press Professional, Inc., San Diego, CA, USA, 1990.