Da teorema-esempio-controesempio ad una matematica della sperimentazione
Relazione tenuta dal Prof. Fausto Saleri nel 2001 al convegno del Pristem "Le direzioni del cambiamento. L'insegnamento della Matematica dopo le riforme".
In questa relazione vorrei presentare, attraverso l'esperienza dei corsi di Analisi Numerica tenuti presso il Politecnico di Milano e l'Università degli Studi di Milano, il tentativo di adeguare l'insegnamento della Matematica, ed in particolare della Matematica Applicata, alle nuove esigenze richieste dalle lauree triennali (specialmente per i corsi di Laurea in Ingegneria ed in Matematica).
La riforma universitaria ha comportato un considerevole cambiamento nell'insegnamento della Matematica del biennio, non solo in termini quantitativi (una riduzione rilevante dei programmi), ma, soprattutto, in termini qualitativi (un modo diverso di proporre la materia che, secondo il punto di vista qui esposto, dovrebbe partire dalle sue numerose applicazioni). In questa nota voglio illustrare brevemente l'esperienza maturata nei corsi di Analisi Numerica offerti dal gruppo nel quale lavoro. Sono riflessioni maturate negli ultimi cinque anni tenendo corsi sia presso l'Università degli Studi di Milano, Facoltà di Scienze Matematiche Fisiche e Naturali (corso di laurea in Matematica), sia presso il Politecnico di Milano, Facoltà di Ingegneria (corsi di laurea in Ingegneria Meccanica ed Aerospaziale e corsi di diploma). Vorrei sottolineare che, pur essendo l'Analisi Numerica spontaneamente orientata verso gli aspetti applicativi della Matematica, ciò non toglie che gli spunti che seguono possano essere opportunamente estesi ad altri settori della Matematica, da sempre ritenuti di carattere più teorico.
Due sono i fattori dei quali dovremmo tener conto per impostare una didattica nuova della Matematica: il nuovo sistema universitario ed il notevole sviluppo del software di calcolo simbolico, congiuntamente alla sempre crescente diffusione della Matematica Computazionale.
Nel nuovo sistema universitario, organizzato in due cicli consecutivi, il punto più critico è certamente dato dalla laurea triennale e dagli obiettivi che essa si prefigge. In effetti, per quanto riguarda ad esempio la laurea in Matematica o quella in Ingegneria Matematica, il nuovo laureato dovrebbe essere un tecnico di alto profilo richiesto da industrie, da centri di elaborazione dei dati, dalle banche, dalle società assicurative, informatiche o telematiche, dalle strutture scolastiche. Da un'indagine ISTAT effettuata nel 1998 sui laureati del 1995 risulta che più del 60% dei laureati in Matematica trovi lavoro come lavoratore in proprio, tecnico di alta/media qualificazione, impiegato esecutivo (il 36% come insegnanti, il 5% come dirigenti e quadri). Di conseguenza, la figura professionale che emerge richiede una visione interdisciplinare della materia (dalla quale devono emergere i modelli, deterministici, aleatori e computazionali), accompagnata da solide basi matematiche (per impiegare e sviluppare i modelli). Solo in questo modo si potrà raggiungere l'obiettivo ultimo che consiste nel rapido inserimento nel mondo del lavoro (a 22 anni) del laureato. Il problema principale che si riscontra è costituito dal poco tempo a disposizione dello studente per gli approfondimenti e la riflessione personale. La visione costruttiva dei metodi matematici ed il maggior coordinamento fra i docenti può ovviare però significativamente a questa difficoltà, dando un quadro d'insieme unitario. Vorrei a questo proposito riportare l'esperienza (si veda la Figura 1 ) di coordinamento maturata al Politecnico di Milano fra i corsi di Analisi A (I semestre, I anno), Analisi B e Calcolo Numerico (II semestre, I anno). Gli allievi ingegneri ritrovano lo stesso argomento prima in Analisi e successivamente in Calcolo Numerico in modo da aver più tempo per consolidare la loro conoscenza di un argomento ed evitando ripetizioni. È importante notare come tutti e tre i corsi si siano orientati verso l'uso di un unico prodotto software, Matlab nel nostro caso, nel quale far esercitare gli strumenti al calcolatore.
Il cenno fatto al programma Matlab ci conduce verso il secondo aspetto che ha cambiato recentemente la didattica della Matematica: il software di calcolo simbolico e, più in generale, il software matematico oggi a disposizione. In effetti, a partire dal 1988 quando apparvero Maple 4.2 per workstation e mainframe e Mathematica 1.0, la quantità e la qualità del software matematico è enormente aumentata (si veda, ad esempio, il sito sal.KachinaTech.com). Questa esplosione è certamente dovuta da un lato all'enorme aumento della potenza di calcolo dei microprocessori (si veda la Figura 2 ), dall'altro all'affinarsi delle tecniche di
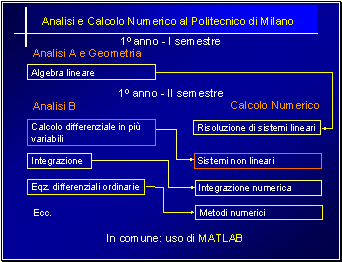
Figura 1 . Un esempio di programmi coordinati al prim'anno
programmazione e di analisi di questo tipo di prodotti. Il nuovo software matematico si contrappone alle librerie di software tradizionali, caratterizzate da una forte specializzazione, e si propone come un ambiente di sviluppo ed esecuzione fortemente integrato (calcolo scientifico, calcolo simbolico, visualizzazione). Esso pone il docente di fronte ad alcune preoccupanti domande su quanto sia ancora essenziale insegnare determinate tecniche di calcolo.
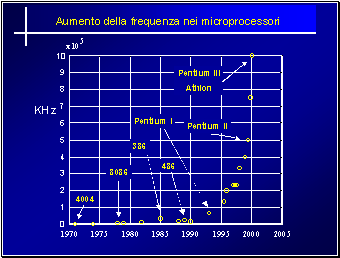
Figura 2 . Aumento della frequenza nei microprocessori
Vediamo un esempio: il toolbox (cioè un insieme di programmi destinati alla risoluzione di uno specifico problema) funtool di Matlab. Già semplicemente invocandone l'help lo studente si trova di fronte a questo accattivante messaggio:
>> help funtool
FUNTOOL A function calculator.
FUNTOOL is an interactive graphing calculator that manipulates
functions of a single variable. At any time, there are two
functions displayed, f(x) and g(x). The result of most
operations replaces f(x).
In effetti, una volta eseguito il commando, il programma propone l'interfaccia grafica di Figura 3 , attraverso la quale lo studente può introdurre la funzione da studiare, integrare, derivare o combinare variamente con altre funzioni. Con uno strumento di questo genere, un corso del biennio di introduzione all'Analisi potrà valorizzare maggiormente gli aspetti concettuali (la continuità, la derivabilità, le regole elementari di calcolo, ecc.), delegando gli aspetti più tecnici (calcolo delle radici di una funzione, di integrali complicati e via dicendo) al software.
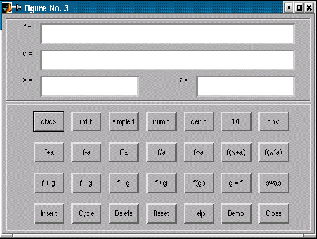
Figura 3 . L'interfaccia grafica del comando Matlab funtool
Questo fatto non snatura l'operato del docente, anzi consente di evidenziare i limiti del software utilizzato e, di conseguenza, l'importanza della teoria retrostante. Non si possono perciò ignorare strumenti di questo genere da un lato perché la loro diffusione è destinata a crescere rapidamente (alcuni di essi, come Cinderella per la Geometria, sono già a disposizione sui PocketPC), dall'altro perché la loro penetrazione nel mondo del lavoro è in costante aumento. È quindi importante preparare laureati capaci di usare in modo critico questi applicativi in modo da trarne il massimo profitto. Un'esperienza interessante a questo proposito è il corso di Laboratorio di Matematica Computazionale da me tenuto nell'A.A. 2000/01 per il corso di laurea in Matematica dell'Università degli Studi. Il corso, obbligatorio per gli studenti del primo anno e collocato nel II semestre, era privo di esame e si caratterizzava per la sua trasversalità rispetto alle altre materie del prim'anno. Lo studente ad ogni lezione veniva messo di fronte ad un problema concreto (tipicamente una versione semplificata di un problema reale come la compressione delle immagini, problemi di crittografia, ecc.), agli strumenti matematici che si potevano usare per la sua risoluzione e ad un suggerimento. L'allievo era poi lasciato libero di trovare una soluzione al problema proposto, generalmente da implementare poi al calcolatore con l'ausilio di Matlab. Nella prima parte della lezione seguente si discuteva la soluzione proposta dal docente e la si confrontava con quelle proposte dagli studenti. Il lavoro in gruppo (due o, al più, tre studenti) non solo non era proibito, ma invogliato. Uno degli obiettivi raggiunti è stato quello di motivare maggiormente gli studenti ad approfondire la Matematica nel sui insieme e a cogliere le correlazioni tra le sue componenti grazie al fatto che gli allievi stessi si sento responsabilizzati a risolvere un problema reale mettendo a frutto quello che hanno appreso nei vari corsi seguiti. Inoltre, l'implementazione al calcolatore li spinge ad approfondire liberamente gli aspetti della programmazione che spesso nei corsi tradizionali appaiono come una forzatura imposta dal docente. Naturalmente lezioni di questo tipo sono pesanti da sostenere e possono essere realizzate con classi di dimensioni contenute (nel caso in questione si trattava di una quarantina di allievi).
A partire dalle riflessioni dettate da questa esperienza emerge naturale un modo di far lezione che superi lo schema classico teorema-esempio-controesempio. Il punto di partenza è un problema realistico che si presti ad introdurre l'argomento della lezione. Segue quindi un tentativo di soluzione che può essere condotto sia con tecniche analitiche, sia avvalendosi di software opportuno. In questa fase vengono evidenziate le difficoltà intrinseche al problema in esame. L'astrazione e la f ormalizzazione del modello matematico retrostante viene a questo punto naturale, così come naturale avviene l'introduzione delle proprietà principali, esemplificate da esempi essenziali. La lezione si conclude con una rivisitazione del problema di partenza alla luce delle riflessioni effettuate. Vorrei fornire un'esemplificazione di questo modo di procedere su un argomento specifico della materia che insegno, l'Analisi Numerica: la risoluzione di equazioni non lineari con metodi iterativi proposta a studenti di Matematica o di Ingegneria, con riferimento ai cambiamenti apportati nel gruppo di docenti nel quale lavoro sul modo di proporre l'argomento.
Nella struttura universitaria tradizionale l'Analisi Numerica si situava tra il terzo ed il quart'anno del corso di studi (al Politecnico di Milano per molti corsi di laurea era situata proprio al terz'anno) e si rivolgeva conseguentemente a studenti già formati dal punto di vista delle conoscenze di base della Matematica. Nella lezione si partiva motivando brevemente l'argomento, spesso in termini puramente matematici (come ad esempio, "Ora ci occupiamo ora della determinazione delle intersezioni del grafico di una funzione con l'asse delle ascisse"). A questo punto si formalizzava il problema, data
trovare a e tale che ,
e si richiamavano i principali risultati dell'Analisi Matematica. L'introduzione dei metodi numerici, che rappresentano in questo caso l'obiettivo della lezione, avveniva generalmente per gradi, dai più semplici ai più complessi, riportandone (e talvolta dimostrando) le principali proprietà teoriche. Raramente si riuscivano ad affrontare problemi realmente interessanti (come la risoluzione di sistemi lineari con tecniche moderne effettivamente usate). Ciò nonostante la lezione raggiungeva il suo scopo perché lo studente, specialmente in ambito matematico, avrebbe poi avuto la possibilità di accedere a corsi più avanzati e specifici nei quali approfondire alcune tematiche, qui solo accennate. Accanto alla lezione si sviluppava l'esercitazione, generalmente al calcolatore e spesso di tipo frontale: essa aveva come scopo l'insegnamento di un linguaggio di programmazione (nel nostro caso Matlab) e la verifica al calcolatore delle proprietà incontrate durante le lezioni. L'esame si configurava generalmente in una prova scritta ed in una orale, precedute da due prove in itinere.
Vediamo ora come abbiamo mutato questo modo di procedere nelle nuove lauree triennali. L'esperienza che riportiamo si riferisce agli A.A. 2000/01 e 2001/02 per corsi con 3 ore settimanali di lezione e 3 ore di laboratorio (non di esercitazioni), tenuti sia all'Università degli Studi (con classi da 40-50 studenti), sia al Politecnico di Milano (con classi da 130-170 studenti). Il primo punto della lezione è dato dalle motivazioni introdotte partendo dall'analisi di un problema reale, opportunamente semplificato. Ad esempio, si considera il problema di individuare in una sezione di una strada illuminata da due lampioni, il punto di minima illuminazione (si veda la Figura 4 ). Sulla base di semplici considerazioni fisiche si ricava il modello matematico della forma Le conoscenze di base dell'Analisi Matematica consentono di concludere che la risoluzione del problema richiede la determinazione delle radici della derivata prima di F, derivata che può essere calcolata anche avvalendosi del toolbox di calcolo simbolico presente in Matlab o in Maple. È istruttivo provare a far risolvere simbolicamente l'equazione non lineare con uno di questi pacchetti: il sistema non fornisce alcuna risposta rivelando gli inevitabili limiti e, di conseguenza, la necessità di introdurre altre metodologie, di questo tipo di software. A questo punto la lezione può incanalarsi nuovamente nella lezione tradizionale, fornendo le principali proprietà teoriche del modello matematico: la differenza rispetto a prima sta nelle motivazioni. Un analogo discorso vale per la parte propriamente numerica.
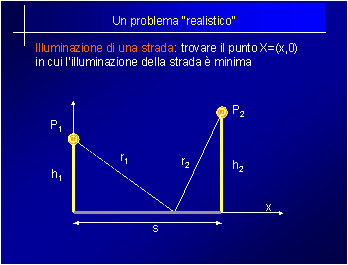
Figura 4 . Il problema di partenza
Solo pochi metodi, effettivamente utilizzati, vengono presentati agli allievi. L'attenzione si sposta dalle proprietà teoriche (comunque presenti, ma evitando le dimostrazioni fini a se stesse) agli aspetti computazionali, mostrando durante la lezione con l'ausilio di un portatile i metodi presenti in azione sul problema reale di partenza. In quest'ottica le esercitazioni in Laboratorio informatico appaiono come la naturale continuazione della lezione. Si tratta di laboratori, non di esercitazioni frontali, nei quali lo studente è invitato a lavorare in maniera individuale affrontando e risolvendo autonomamente i problemi che gli vengono proposti. Gli esercitatori si limitano ad esporre il problema e a dare qualche suggerimento all'inizio dell'esercitazione, nonché ovviamente a rispondere a domande o richieste di chiarimento. L'esercitazione stessa è disponibile via web (si veda il sito www1.mate.polimi.it/CN) fin dall'inizio dell'anno in modo che lo studente possa avere un quadro d'insieme; dalla esercitazione successiva, viene corredata della soluzione in modo che gli allievi possano verificare direttamente la qualità del lavoro che hanno svolto. In queste esercitazioni non si cerca necessariamente la verifica delle proprietà teoriche viste a lezione (a meno che nonm venga naturale), né si usano i soli algoritmi introdotti dal docente del corso. Si cerca di familiarizzare lo studente anche con algoritmi presenti in Matlab, ma troppo complicati da illustrare in corsi così compressi. Questo per condurre lo studente all'utilizzo consapevole di programmi di tipo black-box che, facilmente, si troverà ad utilizzare in ambito lavorativo. La valutazione finale avviene attraverso due prove in itinere, condotte in aule informatizzate, e costituite da un esercizio, simile a quelli proposti durante il corso, e da alcune domande di teoria. A guardare le valutazioni della didattica ricevute in questi ultimi due anni sembra che questo modo di insegnare incontri il gradimento degli studenti: non solo non abbiamo avuto un calo considerevole della frequenza (specialmente alle esercitazioni), ma i risultati ottenuti (più del 50% degli allievi promossi senza ricorrere ai recuperi) sono incoraggianti.
Per concludere, il superamento del paradigma tradizionale teorema-esempio-controesempio sembra ormai inesorabile e la sua sostituzione con un paradigma allargato (problema-modello-teorema-esempio-verifica) sembra invogliare maggiormente lo studente a studiare e ad approfondire i concetti di base della Matematica e a pensare in termini di modelli matematici da analizzare e risolvere. L'uso congiunto di opportuno software matematico getta inoltre le basi di una conoscenza critica di questo genere di strumenti che, a mio parere, diverranno sempre più importanti nei settori di sbocco delle lauree in Matematica ed Ingegneria.
