Intervista a Martin Gardner il "giocoliere della matematica"
Martin Gardner, il più autorevole e prolifico scrittore di matematica ricreativa di ogni epoca e paese, è nato il 21 ottobre 1914 a Tulsa in Oklahoma (entro il 2004, quindi, arriverà a compiere la ragguardevole età di 90 anni). Dal 1956 al 1981, ha curato, per il mensile Scientific American, una rubrica di enigmi e giochi matematici, divenuta popolare in tutto il mondo (in Italia, è stata riproposta da Le Scienze). Ha pubblicato, inoltre, centinaia di articoli su varie riviste e ha scritto più di settanta libri, di argomenti che spaziano dalla scienza alla filosofia, dalla matematica alla letteratura.
Una delle sue principali caratteristiche consiste nel riuscire a visitare, con la leggiadria di un giocoliere, anche le più complesse branche della Matematica, trovando sempre degli spunti curiosi e coinvolgenti. Contrariamente a quanto si potrebbe credere, però, Martin Gardner non ha compiuto studi scientifici; l'unico titolo scolastico che possiede è un diploma di Filosofia, conseguito presso l'Università di Chicago nel 1936. La sua cultura matematica è completamente autodidatta e trae origine dalla passione per i giochi di prestigio, che coltiva fin da bambino, e da un'innata curiosità nei confronti delle tematiche trascendenti. Il suo primo libro, Fads and Fallacies in the Name of Science, pubblicato nel 1952 (tradotto in italiano, nel 1998, con il titolo di Nel Nome della Scienza: uno studio sulla credulità umana, dalle Edizioni Transeuropa di Ancona), analizza e smantella più di cinquanta generi di credenze pseudoscientifiche nel campo del paranormale.
Sempre nel 1952, Martin Gardner iniziò a collaborare con l'Humpty Dumpty's Magazines, un giornale per bambini, per il quale, oltre a scrivere racconti fantasiosi, disegnava degli originali giochi di carta, come quello riportato qui di seguito.
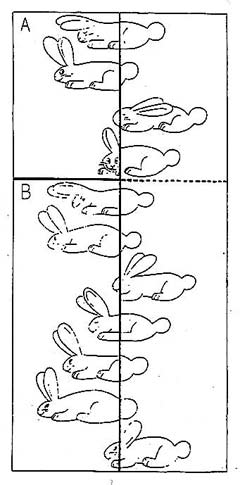 Figura 1 |
|
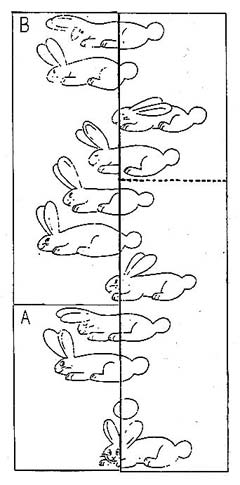
Nella figura 1 sono raffigurati 11 coniglietti. Se, però, si ritagliano i due rettangoli contrassegnati con le lettere A e B e si scambiano di posto, misteriosamente un coniglio scompare e si trasforma in un ovetto, come indicato in figura 2.
Questa particolare esperienza (durata otto anni) contribuì ad affinare le sue doti di narratore fantasioso, ma soprattutto lo abituò a scrivere in modo chiaro, semplice e diretto.
Qualche anno dopo, nel 1956, prima di iniziare la sua collaborazione con Scientific American, Gardner pubblicò Mathematics, Magic and Mistery (tradotto in italiano con il titolo di I misteri della magia matematica, nel 1985 dalla Sansoni di Firenze), un'originale opera che raccoglie e classifica i più interessanti giochi di prestigio, basati su un ragionamento matematico, e che costituisce una sorta di manifesto della Matemagica (termine coniato, nel 1951, dal mago Royal V. Heat).
Uno dei più affascinanti problemi divulgati da Martin Gardner, nel corso della sua lunga carriera, può considerarsi il seguente, proposto nella versione tratta da un suo articolo rievocativo, pubblicato in italiano, nel numero 362, ottobre 1998, de Le Scienze.
|
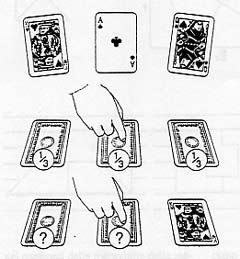
| Jones, un giocatore d'azzardo, mette tre carte coperte sul tavolo. Una delle carte è un asso; le altre sono due figure. Voi appoggiate il dito su una delle carte, scommettendo che sia l'asso. Ovviamente, la probabilità che lo sia realmente è pari a 1/3. Ora Jones dà una sbirciatina di nascosto alle tre carte. Dato che l'asso è uno solo, almeno una delle carte che non avete scelto deve essere una figura. Jones la volta e ve la fa vedere. A questo punto, qual è la probabilità che ora il vostro dito sia sull'asso? |
Soluzione
Molti pensano che la probabilità sia salita da 1/3 a 1/2. Dopo tutto, ci sono solo due carte coperte, e una deve essere l'asso. In realtà la probabilità rimane 1/3. La probabilità che non abbiate scelto l'asso rimane 2/3, anche se Jones sembra aver eliminato parzialmente l'incertezza mostrando che una delle due carte non prescelte non è l'asso. La probabilità che l'altra delle due carte non prescelte sia l'asso, tuttavia, resta uguale a 2/3, perché la scelta era avvenuta prima. Se Jones vi desse l'opportunità di spostare la vostra scommessa su quella carta, dovreste accettare (sempre che non abbia qualche carta nella manica, naturalmente).
Martin Gardner presentò per la prima volta questo problema, nell'ottobre 1959, in una formulazione diversa (al posto delle tre carte, c'erano tre prigionieri, uno dei quali era stato graziato dal governatore locale). Nel 1990 Marilyn vos Savant, autrice di una popolare rubrica sulla rivista Parade, ne propose un'ulteriore versione (che contemplava tre porte, dietro le quali si celavano un'automobile e due capre). La vos Savant fornì la risposta corretta, ma ricevette migliaia di lettere infuriate (molte delle quali, inviate da docenti di matematica…) che l'accusavano di ignorare la teoria delle probabilità. Il caso finì in prima pagina sul New York Times e il problema acquistò in breve tempo una popolarità planetaria, arrivando a essere valutato come il più bel paradosso probabilistico del secondo millennio.
Nota - L'elenco completo delle edizioni italiane delle opere di Martin Gardner è riportato nel volumetto: Lo specchio di Martin - Guida a "Enigmi e giochi matematici" e dintorni, a cura di Consolato Pellegrino, Pitagora Editrice, Bologna, 2003, pp. 40, 3,50.