Mandelbrot e la geometria frattale
"Vanno vengono, ogni tanto si fermano e quando si fermano sono nere come il corvo sembra che ti guardano con malocchio. Certe volte sono bianche e corrono e prendono la forma dell'airone o della pecora o di qualche altra bestia ma questo lo vedono meglio i bambini che giocano a corrergli dietro per tanti metri."
Fabrizio De André, "Le nuvole"
Come i bambini nella canzone di De André, Benoît B. Mandelbrot, nella sua vita di matematico fuori dagli schemi, ha cercato di cogliere il segreto delle loro forme e c'è riuscito.
Nato in Polonia nel 1924 da una famiglia ebrea borghese di origine lituana con il culto del successo individuale, a causa degli avvenimenti storici che prima coinvolsero la Polonia e la sua famiglia, poi il mondo intero con la seconda guerra mondiale, dovette conoscere più volte l'amara esperienza di essere uno straniero dapprima in Francia e poi in America, esperienza che nella sua formazione si estese dalle nazioni all’ambito scientifico essendo stato per lungo tempo un nomade delle istituzioni accademiche. Una traiettoria di vita non lineare, con una successione di eventi – per alcuni versi tempestosi seguiti da altrettanti momenti fortunati – che hanno costituito un segno del destino, quello di convergere le sue ricerche inizialmente slegate e frammentate verso la … rugosità.
Alla fine della seconda guerra mondiale, il giovane e promettente Mandelbrot apprende dallo zio Szolem Mandelbrojt (1899-1983), affermato matematico al Collège de France e purista della scienza, della graduale decadenza della geometria (da lui tanto amata) in favore di una sempre più spinta tendenza all'astrazione algebrica. Se voleva quindi dare qualche contributo originale alla ricerca matematica doveva abbandonare il suo entusiasmo giovanile per la geometria e seguire, all'École Normale Supérieure, le tracce del gruppo sempre più influente costituito attorno al brillante matematico André Weil (1906-1998), capo carismatico del gruppo di matematici intitolato a Bourbaki. Per tutta risposta, superati brillantemente gli esami sia all'École Normale che all'École Polytechnique, Mandelbrot resiste solo un giorno alla Normale e decide di iscriversi all'École Polytechnique, scuola di altissimo livello di stampo militare. Qualche anno dopo e a seguito di una seconda "lavata di capo" da parte dello zio Szolem, Mandelbrot avvia la sua tesi di dottorato e riscopre le opere di Gaston Julia (1893-1978) e Pierre Fatou (1878-1929), matematici che avevano formulato negli anni '10 del Novecento la teoria iterativa della dinamica non lineare. È in questo frangente che inizia la trentennale riflessione su tale teoria e che lo porterà a scoprire la sua immagine più rappresentativa: l'insieme di Mandelbrot.
Dopo alcune esperienze e vagabondaggi in varie università americane, Mandelbrot lascia il percorso accademico e viene assunto alla IBM. In azienda, come spesso dichiarerà, si trova a suo agio e riesce a mantenere e coltivare quella sensibilità geometrica e visiva che lo ha caratterizzato fin da giovane. Qui accumula una notevole quantità di materiali, inizialmente eterogenei, che trovano nella sua pubblicazione più famosa "The Fractal Geometry of Nature" uno sbocco unitario.
Funzioni quali la curva di Giuseppe Peano (1858-1932) che ricopre interamente un quadrato o quella di Karl Weierstrass (1815-1897) priva di derivata in tutti i suoi punti, accantonate da accademici ancora legati alle classiche ipotesi di regolarità e da questi dichiarate come patologiche e controintuitive, furono da Mandelbrot reinterpretate e, con la sua intuizione geometrica, affiancata successivamente dalla grafica al computer, divennero gli strumenti di base di una nuova scienza, quella della rugosità.
La curva di Peano che, al limite, ricopre un quadrato
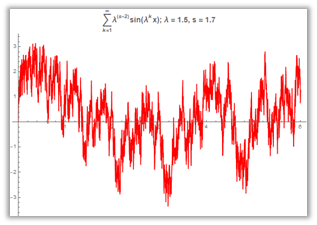
La curva di Weierstrass, ovunque continua ma mai derivabile
Fenomeni quindi apparentemente impossibili da ricondurre a uno schema matematico, quali i profili di una montagna o le linee costiere, la forma delle nuvole o le ramificazioni di una pianta, trovano nella geometria frattale di Mandelbrot una adeguata descrizione e un modello matematico di riferimento. La caratteristica più notevole di questa geometria è che permette di imitare la natura: se l'ordine rarefatto della geometria di Euclide, fatta di poligoni e cerchi, appare da un lato lontano dal caos delle forme naturali per cui, come scrive Mandelbrot è ovvio che "le nuvole non sono sfere, le montagne non sono coni, le linee di costa non sono dei cerchi e la corteccia non è liscia, né la luce viaggia in linea retta", il nuovo paradigma permette invece di ristabilire una relazione tra gli oggetti reali e le loro formalizzazioni matematiche cioè le figure. La nuova "lingua", la geometria frattale, è quindi lo strumento appropriato per descrivere la rugosità del mondo reale e la complessità delle sue forme e configurazioni. Così, se grazie a Cartesio (1596-1650) le forme euclidee sono comunemente descritte da una semplice formula algebrica qual è quella della circonferenza x2+y2=1, gli oggetti frattali sono generalmente il risultato di una procedura o un algoritmo ricorsivo che richiama ripetutamente sé stesso.
È così che si comprende come la natura costruisce, per esempio, la foglia di felce: se si compongono ripetutamente quattro semplici trasformazioni affini, ciascuna descritta da sei numeri, la forma che emerge al procedere del calcolo eseguito da un computer (tecnicamente detta attrattore), è appunto la ben nota foglia con le sue ramificazioni. Ma se osserviamo con attenzione la sua struttura cogliamo pure una fondamentale caratteristica dei frattali e quindi anche delle forme naturali: essa appare autosimile, ossia una sua parte riproduce in scala minore l'intera struttura della foglia.

La foglia di felce e un suo particolare ingrandito
Una forma è quindi autosimile se è composta di copie di sé stessa in scala ridotta. Comprendiamo ora l'origine del termine frattale, neologismo coniato dallo stesso Mandelbrot rifacendosi alle sue conoscenze giovanili di latino: fractus ossia rotto, spezzato, di forma irregolare e frammentata. Un oggetto frattale può quindi essere scomposto in parti sempre più minute, ma la sua rugosità rimane sostanzialmente inalterata.
Questa caratteristica lo distingue perciò in modo sostanziale dalle classiche funzioni che si studiano negli ultimi anni di scuola superiore: qualsiasi sia il loro andamento, anche molto complesso, se osservate a ingrandimenti sempre più spinti, si riducono a semplici tratti rettilinei e perdono quindi la loro iniziale complessità. Sebbene matematici come Gaston Julia, Pierre Fatou, Felix Hausdorff (1868-1942) abbiano fornito contributi importanti allo studio di insiemi parzialmente ordinati, è merito di Mandelbrot l'aver introdotto una teoria matematica in grado di ricomporre un ordine dove prima c'erano solo complessità e caos.
I frattali mostrano forme complesse, ma la loro comprensione si ottiene a partire da regole semplici adeguatamente ripetute: come la foglia di felce, un fiocco di neve appare in una infinità di forme ed è un oggetto reale, ma la matematica frattale permette di astrarre le sue caratteristiche e di scoprire la semplicità che sta alla base delle leggi che lo formano.
In questo senso l'idealizzazione permette di cogliere proprietà importanti della realtà pur essendo questa sempre approssimata. Il grado di irregolarità o di frammentazione di un frattale, in ultima analisi la sua rugosità, viene letteralmente misurato da un parametro che costituisce la dimensione frattale dell'oggetto. Diversamente dalle nozioni di geometria elementare, dove la dimensione di un oggetto non può che essere un numero intero cioè 1 per una linea, 2 per un quadrato (ma pure 2 per la curva di Peano conforme al fatto di ricoprire a sua volta un quadrato), 3 per un cubo, la dimensione frattale assume, in questa teoria, valori di norma frazionari: 1,262 è la dimensione frattale del fiocco di neve o curva di Helge von Koch (1870-1924), che prima di Mandelbrot era classificata tra le curve patologiche perché priva di tangente in ogni suo punto e di lunghezza infinita.

La curva di von Koch o fiocco di neve
La dimostrazione che da ipotesi semplici, seguite da procedimenti numerici altrettanto semplici, possano scaturire forme di sbalorditiva complessità e ricchezza di particolari, si ottiene considerando l'insieme che proprio da Mandelbrot prende il nome e che lo ha reso universalmente noto.

L'insieme di Mandelbrot nella sua interezza
Questo oggetto matematico è visualizzabile a partire da un punto z sul piano complesso e quindi con una semplice regola del tipo f(z)=z2+c con c costante, si ottiene la posizione del punto successivo iterando il procedimento. Colorando opportunamente i diversi stadi di tale calcolo, si giunge a un oggetto frattale incredibilmente complicato. Se si ingrandisce una porzione del suo bordo, anziché trovarlo rettilineo, emergono immagini sempre più barocche e ricche di particolari e di riconosciuta bellezza estetica.
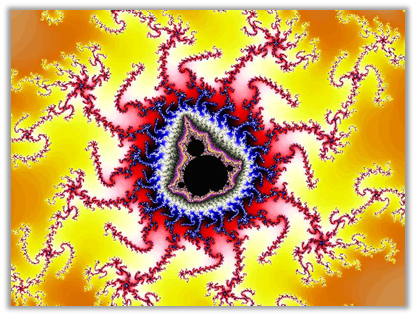
Particolare dell'insieme di Mandelbrot ingrandito 300 mila volte

Particolare dell'insieme di Mandelbrot
A qualsiasi scala vi si scoprono continuamente copie microscopiche dell'intero insieme in un intrico infinito di configurazioni, filamenti e strutture. Nell'insieme di Mandelbrot la componente caotica delle sue raffinate strutture non prevale sulle ampie regioni, dove invece regna la regolarità. Caos e ordine mostrano un armonico equilibrio che, nel loro mescolarsi e fondersi, affascina e coinvolge. Un tale oggetto ha dato origine a numerose congetture matematiche sulle sue proprietà e a sfide intellettuali che spaziano nei campi, non solo della matematica e della fisica, ma pure della biologia, della teoria dell'informazione e, non ultima, dell'arte.
Nelle forme naturali, siano esse un susseguirsi di montagne, un rincorrersi di nuvole, l'alternanza di boschi e radure, o cristalli di neve, il nostro senso estetico riconosce una combinazione armoniosa di ordine e disordine. Forse, il merito di Mandelbrot consiste nell'averci liberato da una descrizione della realtà circoscritta a sistemi artificiali scelti per la loro regolarità, fornendoci invece gli strumenti per collegare la comprensione scientifica con l'esperienza estetica che discende dall'irregolarità e dall'imprevedibilità insite nella natura. Affiancando dunque queste forme di conoscenza, possiamo apprezzare ancora, e meglio, i versi di De André: "Vanno, vengono, per una vera mille sono finte e si mettono lì tra noi e il cielo per lasciarci soltanto una voglia di pioggia".
Riferimenti bibliografici
[1] Mandelbrot B. B., La formula della bellezza, Rizzoli, 2014.
[2] Mandelbrot, B. B., The Fractal Geometry of Nature, W. H. Freeman & Co., 1983.
[3] Falconer K., Fractal Geometry: Mathematical Foundations and Applications, Wiley, 2nd ed., 2003.
