TASSELLI REGOLARI ED IRREGOLARI
Dal microscopico al macroscopico, la natura applica i principi d’economia ed ottimizzazione.
Nella filosofia d’Aristotele, la forma (morphé) era definita la ragion d’essere delle cose, ciò che fa sì che le cose siano ciò che sono: era considerata causa capace di fare uscire l’essere dall’indeterminazione conferita dalla materia. Apprezzata come un’essenza intrinseca, era la sostanza fondamentale delle cose sensibili, il principio organizzatore della materia, ciò che spiega come la materia giunga a comporsi. Kant definì la forma come il determinante e la materia come il determinabile: la forma è ciò che permette di ordinare i dati sensoriali. Dal secolo XVIII, il concetto di forma fu considerato in estetica per indicare l’elemento distintivo dell’opera d’arte. La forma artistica va ad aggiungersi ad un contenuto materiale o concettuale, mentre la forma naturale è un mero aspetto contingente delle cose.
Lo studio dell’aspetto esteriore di un oggetto, sia foggiato dalla natura sia dall’uomo, può essere espresso in modo descrittivo oppure simboleggiato attraverso il metodo analitico, utilizzando il linguaggio matematico. L’applicazione di concetti astratti ad oggetti reali può rendere concrete proprietà e relazioni di tangibilità del mondo esterno, mediante i postulati geometrici (un sistema di proprietà primitive e d’operazioni possibili), con le misteriose congruenze ed interrelazioni del pensiero logico. Le definizioni e i postulati, le operazioni astratte della Geometria traducono i procedimenti empirici in oggetti naturali e in figure concrete. Nell’antichità, la Geometria ebbe inizio per esigenze pratiche di misura di terreni e divenne solo in seguito il modello della scienza organizzata deduttivamente, collocandosi a fondamento dell’indagine della natura e della conoscenza. Il ragionamento geometrico può essere, dunque, considerato il primo pensiero scientifico.
Le prime forme regolari che si mostrarono all'uomo furono la retta e il cerchio: con loro nacque la Geometria. Le testimonianze degli storici indicano i suoi albori in Egitto. I primi geometri dell'antichità furono, infatti, gli agrimensori: tirando le funi, i geometri egizi potevano tracciare sul terreno rette e cerchi, un'operazione di cui resta una traccia in molte lingue moderne, nell'espressione tirare una retta.
Il primo vero e proprio testo di Geometria, che pervenne nella sua completezza, furono gli Elementi d’Euclide (IV sec. a.C.), dove le proprietà geometriche delle figure vennero dimostrate partendo da proposizioni primitive: assiomi e postulati. Euclide costruisce una Geometria rigorosa fondandola su pochi enti astratti (punto, retta, piano), elencando verità che non devono essere dimostrate e derivando da loro tutte le proprietà geometriche.
Gli Elementi sono un'opera organizzata secondo il procedere assiomatico-deduttivo proprio del pensiero greco (e, di lì poi, di tutta la matematica occidentale) attraverso principi, definizioni e postulati. Il testo greco rappresenta una proposizione primitiva di una teoria, assunta senza dimostrazione, che notoriamente ha la funzione di tradurre in simboli e forme geometriche gli oggetti e i procedimenti del mondo reale.
I primi tre postulati riproducono esattamente le operazioni dell'agrimensore egiziano:
- condurre una linea retta da un qualsiasi punto ad un altro punto (tirare una linea retta da un qualsiasi segno ad un qualsiasi altro segno);
- prolungare una retta continuamente (produrre subito dopo per diritto una linea retta finita);
- descrivere un cerchio con qualsiasi centro (con qualsiasi centro e intervallo descrivere un cerchio).
Il quarto afferma che: - tutti gli angoli retti sono uguali tra loro.
Il quinto è il famoso postulato delle parallele: - Se una retta, cadendo sopra altre due rette, forma angoli interni dalla stessa parte minori di due retti, quelle due rette, prolungate, s’incontreranno dalla parte in cui sono gli angoli minori di due retti.
La Geometria euclidea mantenne una posizione dominante fino al secolo XVII, quando Cartesio riuscì a tradurre le figure geometriche in equazioni algebriche, innalzando l’Algebra al vertice della Matematica: nacque la Geometria analitica che, mediante l’impiego di sistemi di coordinate, studia proprietà intrinseche di concetti che si agganciano al significato aristotelico di forma.
All’inizio del XX secolo il biologo scozzese D’Arcy Thompson lanciò l’ipotesi della dinamica dei campi morfogenetici, che si riferisce ai processi di creazione di forme con metodi analitici, e mette in luce il fondamentale ruolo della Matematica intesa come studio di modelli e di regolarità.Nel suo libro Crescita e forma, pubblicato nel 1917, descrisse con parole e disegni il legame che esiste tra le cellule e le foglie, le conchiglie e i fiori, le ossa e gli alberi, mediante la decifrazione visiva delle forze che rappresentano il mondo e che agiscono su tutti i sistemi viventi e non viventi. In uno dei passi, spiega addirittura le configurazioni degli organismi biologici partendo dalle bolle di sapone: le cellule in analogia sono modellate dalla tensione superficiale e assumono la forma che utilizza il minimo d’energia.
L’opera di Thompson rappresentò un input per utilizzare la Matematica anche per l’esame di forme naturali, come procedimento per la descrizione morfologica, come ipotesi di spiegazione d’eventi d’autorganizzazione di crescita, d’ordine e di complessità. In questo periodo, si è propensi ad affermare (secondo . Brian Goodwin) che anche l’evoluzione della vita sia “una danza attraverso il morfospazio, cioè lo spazio delle forme degli organismi”, una danza che segue le leggi della morfologia razionale che generano le forme stabili. Nei suoi scritti, lo studioso canadese propone una nuova concezione, in parte opposta alla concezione dell'uomo di Darwin, che considera l'essere umano interconnesso con l'ambiente in cui è inserito e non una semplice appendice.
Nella vita quotidiana tutto è riconducibile a forme geometriche regolari ed irregolari, semplici o complesse, simmetriche o asimmetriche. Ad esempio, tutto ciò che si muove è simmetrico: uomini, animali, uccelli, aeroplani. La simmetria è sinonimo di stabilità, d’ordine. Anche nelle arti figurative, una struttura simmetrica, intesa come rappresentazione armoniosa di componenti, è sinonimo d’equilibrio. Nell'arte ornamentale, la ripetizione ritmica e continua di un motivo è la più semplice forma che si possa individuare.
Una figura costituita da poligoni che ricoprono l’intero piano, senza sovrapporsi, come in un puzzle, che riproduce ad esempio la piastrellatura di un pavimento, è chiamata dai matematici tassellazione ed è definita come copertura del piano con elementi qualsiasi senza intersezioni e vuoti.
 |
|
Per realizzare una tassellatura regolare del piano, gli elementi essenziali sono i poligoni regolari. La scelta del poligono è ristretta solo al caso di triangoli equilateri, quadrati ed esagoni, con dimensioni scelte a piacere, perché sono gli unici a permettere una tassellatura regolare. Infatti, una figura geometrica regolare può ricoprire il piano solo se l'angolo interno è un divisore di 360°. A questo punto, poiché bisogna replicare la stessa figura in diverse posizioni dello spazio e far aderire le copie tra loro, senza sovrapporle e senza lasciare vuoti, è necessario scegliere l'appropriato movimento rigido: traslazione e rotazione. Riconducibili a traslazioni, rotazioni, ribaltamenti sono le isometrie, trasformazioni in cui si applica uno spostamento nella stessa direzione, nello stesso verso e per tratti nella stessa lunghezza. Una trasformazione è un’isometria quando due figure del piano, che si corrispondono secondo quella trasformazione, sono uguali. Gli schemi bidimensionali, come quelli che si vedono comunemente raffigurati nella carta da parati, nelle piastrelle e nei fregi (soprattutto egizi e moreschi) sono composti applicando ad un unico motivo fondamentale trasformazioni isometriche. Una tassellazione è isometrica se tutti i tasselli hanno la stessa relazione con il resto della tassellazione: dati due tasselli qualunque, esiste un’isometria che sposta localmente uno dei due tasselli nell’altro, ma lascia globalmente invariata la tassellatura.
La tassellatura del piano, mediante riproduzione di un unico motivo fondamentale per trasformazioni isometriche, fu studiato con particolare cura dal grafico olandese M.C.Escher (1898-1972). Il suo interesse a proposito di tale argomento iniziò proprio dall’esame degli elementi compositivi delle decorazioni moresche dell’Alhambra (Granada). In un piano "infinito", anche se delimitato da una circonferenza, Escher operò delle coperture mediante un unico modello ornamentale, ruotando, traslando, e via via rimpicciolendo la figura, secondo un ben preciso processo di riduzione, man mano questa si allontana dal centro verso i margini del "piano".

Quali tassellature regolari si possono riscontrare in natura?
Un esempio di tassellatura regolare è la superficie alare degli insetti: ricoperte da minuscole scaglie disposte in file, che si sovrappongono come le tegole dei tetti. La struttura e la disposizione delle scaglie e il modo in cui riflettono e diffondono la luce danno colorazioni come il bianco, il blu, i riflessi metallici o iridescenti. Il nero, il marrone, il giallo, l'arancione e il rosso, invece, hanno origine chimica e sono dovute a pigmenti. Le ali hanno molteplici funzioni: le facce superiore e inferiore sono strutture che permettono di riscaldarsi al sole, come celle dei pannelli solari. Esistono, poi, scaglie specializzate, che emanano sostanze odorose (i fermomoni), importantissime durante il corteggiamento.
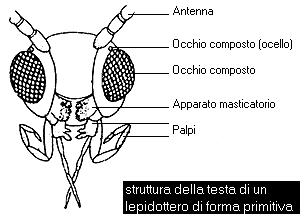
Anche l’occhio composto degli insetti mostra una regolarità geometrica eccellente: è formato da centinaia o migliaia di piccole lenti - gli ommatidi - che forniscono una visione simile a quella di un caleidoscopio, ciascun recante cornea, cono cristallino e pigmenti fotosensibili. Esso permette una visione perfetta in ogni direzione.
Altri esempi sono insiti nel mondo vegetale: il tessuto monocellulare di una cipolla, ad esempio, che al microscopio appare come un pavimento di piastrelle a forma poligonale.
Una mirabile opera di Geometria è il favo delle api, composto di celle a sezione esagonale secondo le leggi di una severa architettura, eseguita con una certa precognizione geometrica. Per costruire le celle, le api percepiscono il campo gravitazionale e il campo magnetico terrestre attraverso sensilli filiformi. Esse costruiscono i favi con cera secreta da otto piccole ghiandole situate sotto l'addome in forma di fluido che solidifica rapidamente. Le scaglie sono raccolte, poi, dalle api operaie con le spazzole del terzo paio di zampe, afferrate dal primo paio e in seguito inumidite con la saliva e lavorate. La composizione chimica della cera è una miscela di oltre trecento sostanze, dove gli idrocarburi, gli esteri e gli acidi sono prevalenti. Per produrre la cera, l'ape consuma enormi quantità di zuccheri, fruttosio, glucosio e saccarosio.

Darwin parla a proposito delle api “del più splendido degli istinti conosciuti”, poiché “il favo delle api è assolutamente perfetto nei riguardi dell’economia di lavoro e di cera”.
La cella, infatti, è un esagono regolare in cui tutti i lati hanno la stessa lunghezza e gli angoli la stessa ampiezza di 120°, in modo che ogni parete serva ogni volta per dividere due celle. Perché, dunque, scegliere la configurazione esagonale?
Le possibilità per costruire le celle sono rappresentate dalle figure geometriche triangolare e quadrata, ma tra queste tre possibilità (triangoli, quadrati, esagoni) si riscontra con semplici calcoli che il perimetro più corto è quello esagonale. Dunque, si consuma meno cera costruendo le celle a sezione esagonale. L’economia in Matematica si traduce nel definire un problema di minimo: la quantità di cera occorrente è minima quando il perimetro di un poligono, di superficie assegnata, è il più piccolo possibile. Le api conoscono, dunque, la soluzione del problema?
Si ha l’impressione, a questo punto, che i principi geometrici riuniscano il mondo naturale in una serie d’uniche morfologie, differenziatesi per parametri e fattori limitanti, motivate da aspetti biologici, chimico-fisici e d’interazione con l'ambiente esterno. In alcuni casi, sembra predominante l’esigenza geometrica di riempimento di tutta la superficie con aree minimali attraverso la tassellatura regolare.
La tassellatura presenta soltanto caratteristiche di regolaritàoppure può essere del tutto priva di proporzione? Per ottenere una risposta, occorre rivolgere attenzione ad una particolare evoluzione di un sistema random, nel quale ogni trasformazione corrisponde ad una variazione del tutto casuale, aleatoria. In sostanza, una deformazione di figure preesistenti, realizzabile con il metodo delle coordinate su cui si basa la “teoria delle trasformazioni”, può condurre ad una tassellatura di tipo irregolare: sottoponendo la figura primaria ad una deformazione si ottiene una nuova figura. Utilizzando il metodo delle coordinate cartesiane, grazie al quale è possibile rappresentare un modello algebrico del piano geometrico e delle relazioni tra i suoi punti e convertire una forma geometrica in numeri e lettere, si può deformare la figura inscritta inizialmente variando le coordinate dei punti del piano.
Per esemplificare in modo assai semplice, si consideri un cerchio inscritto in un reticolo di coordinate equidistanti (secondo l’asse x e y). Se si alterano le dimensioni del sistema allungandolo secondo la direzione di un asse,trasformando così ogni quadrato in un rettangolo, il cerchio sarà deformato in proporzione con la deformazione del sistema. Si ottiene quindi un’ellisse.
In linguaggio matematico elementare: se si sostituiscono gli originari x e y con x1 e cy1, l’equazione originale del cerchio x2 + y2= a2 diverrà x21 + c2y21 = a2che è l’equazione di un’ellisse.
Analoghe deformazioni sul piano cartesiano si possono avere per i poligoni regolari e per i poligoni irregolari, fino a giungere ad unire un numero n di poligoni irregolari secondo una sequenza random, come mostra la seguente costruzione sul piano cartesiano.
La tassellatura irregolare si riscontra frequentemente in morfologie naturali, quali ad esempio, in un terreno argilloso secco, in alcune strutture cellulari animali e vegetali.

Per citare un esempio nel mondo delle piante, i licheni crostosi tendono a ricoprire secondo una tassellatura irregolare aperiodica e a tratti discontinua l’intera superficie del substrato litico o legnoso su cui vive. Se ingrandito in modo opportuno, il lichene crostoso Rhizocarpon geographicum s.l. riporta, anche a diversi livelli d’ingrandimento, una tassellatura tipo random. Infatti, i tasselli esaminati al microscopio presentano essi stessi forma di poligono irregolare con frontiera approssimativamente costruita da una linea spezzata chiusa.
Caratteristiche tassellature irregolari sono disegnate anche dal terreno argilloso secco. L’argilla è una roccia sedimentaria clastica, costituita principalmente da minute particelle colloidali di silicati, associate a detriti finissimi sabbiosi. Il silicio ha la capacità di formare delle strutture atomiche abbastanza simili al carbonio, dove i legami tra gli atomi di carbonio di uno stesso strato sono complanari e diretti a 120°.
Secondo le teorie più accreditate, sembra che le argille non abbiano rivestito un ruolo importante riguardo all’origine della vita sulla Terra, perché costituite da catene di silicio e non da catene di carbonio che formano le molecole organiche degli organismi viventi terrestri. Esse potrebbero in ogni modo essere preponderanti in un’eventuale forma di vita extraterrestre, impostata sul silicio, anziché sul carbonio.
Su una superficie solida rocciosa extraterrestre, si potrà imbattersi nell’analoga morfologia di un terreno desertificato terrestre?
Inoltre, ammettendo che su una superficie solida extraterrestre si dovesse scoprire una tassellatura simile ai terreni argillosi terrestri, riproducendo i parametri di desertificazione ed ottenendo quindi una tassellatura irregolare, potrebbe esistere anche una microscopica superficie tassellata di Rhizocarpon geographicum, organismo lichenico assai resistente alle condizioni estreme?
O ancora: potrebbe essere possibile rilevare la presenza di licheni endolitici, specie che vivono all'interno del substrato e che crescono nello spessore delle rocce?
Alcune risposte saranno confermate nel 2011 dai risultati della missione Rosetta, che incontrerà nel 2011 la cometa 46 P/Wirtanen facendo atterrare, circa un anno dopo, un modulo sulla superficie cometaria. Dotata di ben 21 strumenti scientifici, suddivisi tra l'orbiter (il satellite che orbiterà intorno al nucleo della cometa) e il lander (il modulo che si poserà sul suolo della cometa), Rosetta potrebbe fornire la risposta a vari quesiti.
Se la tassellatura si riscontra dal microscopico al macroscopico, forse anche l’Universo potrebbe essere un insieme di tasselli irregolari o regolari sul piano cartesiano cosmico? Per esempio, si considerino i tasselli di un puzzle (l’Universo) in una scatola. C'è una sola disposizione nella quale i tasselli ricostruiscono l'immagine completa, ma invece c’è un grandissimo numero di disposizioni disordinate. Inizialmente i tasselli del puzzle si trovano nella forma ordinata e disegnano un'immagine perfetta. Se si scuote la scatola, la disposizione si troverà in disordine, ma più si scuote la scatola tanto maggiore è la probabilità che anche questi gruppi si rompano ed è sempre più difficile indovinare la natura dell'immagine che i tasselli dovrebbero riprodurre. Il disordine dei tasselli aumenterà probabilmente nel tempo qualora si parta da una condizione iniziale altamente ordinata.
Si supponga che anche l’Universo parta da uno stato ordinato. Al passare del tempo, il sistema evolverà rispettando le leggi fisiche e il suo stato si modificherà: la probabilità che si trovi ora in uno stato di maggior disordine è elevata e gli stati disordinati sono assai più numerosi. E così il disordine tende ad aumentare nel tempo.
Quindi, anche l’Universo è forse una gigantesca tassellatura irregolare? E forse anche l’Universo è un gigantesco tassello di un’enorme struttura geometrica?
