Un ritratto di Alan Turing

INTRODUZIONE

Alan Mathison Turing nacque a Londra il 23 giugno 1912; nel 1931 fu accettato al King’s College di Cambridge; nel 1937 pubblicò il suo primo articolo scientifico su un problema di Logica matematica: “On computable numbers, with an application to the Entscheidungsproblem” (“Sui numeri calcolabili meccanicamente con un’applicazione al problema della decisione”) nei Proceedings of the London Mathematical Society. La soluzione che propose lo avrebbe reso famoso nel campo della Matematica e dell’Informatica. Durante la seconda guerra mondiale aiutò il suo Paese e gli eserciti alleati producendo un metodo per decifrare i messaggi in codice degli avversari. Il 29 marzo 1951 fu eletto membro della Royal Society, il massimo riconoscimento per uno scienziato nel Regno Unito.

Turing era omosessuale e, in Inghilterra, l’omosessualità era considerata una malattia mentale. Fu processato per questo nel 1952, riconosciuto colpevole e costretto a iniezioni di estrogeni per un anno. L’8 giugno 1954 fu trovato morto nel suo letto dalla domestica: si era avvelenato mangiando una mela intrisa di cianuro di potassio.

Alan Turing alla fermata dell'autobus con altri membri del Walton Athletic Club

L’IDEA DEL CALCOLO MECCANICO

L’articolo del 1937 “Sui numeri calcolabili meccanicamente con un’applicazione al problema della decisione” si sarebbe dimostrato di importanza fondamentale per gli sviluppi del calcolo meccanico e, in seguito, dell’Informatica (Basti pensare che l’equivalente del premio Nobel per l’informatica, si chiama “Premio Turing”. Quando Alfred Nobel istituì il Premio che porta il suo nome nel 1895, i calcolatori non esistevano, né esisteva l’Informatica.). In questo lavoro Turing affronta un problema proposto dal grande matematico David Hilbert nel 1928, l’Entscheidungsproblem, il “problema della decisione”: determinare, se esiste, un metodo meccanico che permetta di stabilire per ogni possibile affermazione matematica se questa è vera oppure no, appunto deciderne la verità. Grazie ai risultati ottenuti da Kurt Gödel nel 1931, era abbastanza chiaro che la risposta al problema della decisione dovesse essere negativa. Ma, per fissare matematicamente questa intuizione, era necessario un passo iniziale di assoluta novità: dare una definizione di "metodo meccanico". È chiaro a tutti che il metodo per moltiplicare due numeri "in colonna" è meccanico e non richiede alcun ingegno, così come tanti altri metodi (il calcolo delle soluzioni di un'equazione di secondo grado, il calcolo della derivata di un polinomio, ecc.), ma come si fa a dimostrare che non c'è nessun metodo meccanico per ottenere un certo effetto? Era necessario definire in generale quali siano tutti i metodi meccanici: Turing fa proprio questo e definisce quelle che, da allora in poi, diventeranno note come le macchine di Turing.

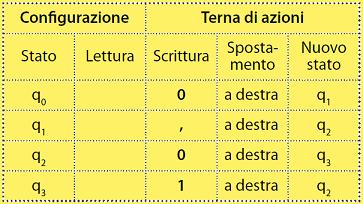
Il passaggio successivo nell’articolo di Turing è quello di notare che le azioni stesse di una qualunque macchina sono “meccaniche”: per eseguire la lista di istruzioni di una macchina è necessario:

• poter riconoscere il simbolo nella casella in lettura;

• accoppiarlo con lo stato della configurazione;

• trovare l’istruzione che coinvolge la configurazione;

• modificare il simbolo;

• modificare lo stato.

Turing ha un’intuizione geniale: il nastro è utilizzato per riportare numeri, scritti cifra per cifra, ma il nastro potrebbe benissimo venir utilizzato per trascrivere istruzioni scritte carattere per carattere. Si potrebbe pensare così di avere una macchina che, se sul nastro è trascritta la lista di istruzioni di una macchina M, produce sul nastro il numero che M stessa avrebbe scritto: tale macchina sarebbe predisposta per eseguire una qualunque macchina di Turing. Proprio per questa caratteristica, Turing chiama tale macchina “universale”. I concetti presentati nell’articolo sui numeri calcolabili sono quelli che oggi troviamo totalmente comuni, nella vita di tutti i giorni, quando ci apprestiamo ad usare un computer: lo stesso strumento (il computer) ci permette di scrivere testi, fare calcoli, disegnare e ben altro (leggere la posta, navigare in internet, ascoltare musica, guardare video, ecc.). E una versione tecnologicamente molto avanzata del nastro di Turing e della sua macchina universale che può eseguire ogni altra macchina. Il nucleo di ogni computer e una macchina universale come quella ideata per prima da Alan Turing.

LE MACCHINE DI TURING

Nell’articolo “Sui numeri calcolabili meccanicamente con un’applicazione al problema della decisione”, Turing scrive che un numero è calcolabile se la sua parte decimale può essere scritta da una macchina.

Turing spiega l’intuizione che guida la sua definizione mantenendo un parallelo con un procedimento umano eseguito pedissequamente, senza “intelligenza”: Per il momento, dirò soltanto che la giustificazione sta nel fatto che la memoria umana è necessariamente finita. Possiamo paragonare un uomo nell'atto di scrivere l’espansione decimale di un numero reale a una macchina che è in grado di considerare soltanto un numero finito di condizioni – diciamo che siano q1, q2, … , qR – che chiameremo “stati”. La macchina è provvista di un “nastro”, (l'analogo della carta per l’uomo) che scorre attraverso di essa ed è diviso in sezioni (chiamate “caselle”) ciascuna in grado di riportare un “simbolo”. In ogni istante c'è esattamente una casella che è “all'interno della macchina". Possiamo chiamare questa la “casella in lettura". Il simbolo nella casella in lettura è detto il “simbolo in lettura". Il simbolo in lettura è l'unico di cui la macchina sia, per così dire, “a diretta conoscenza”.

Per chiarire l’intuizione proposta da Turing usiamo un semplice schizzo del nastro, dello stato e del simbolo in lettura. Il nastro e composto di caselle su cui si possono scrivere i simboli zero 0, uno 1 e la virgola , oppure lasciar bianchi. La casella in lettura e marcato in rosso; sopra di esso viene riportata lo stato nel quale la lettura viene eseguita.

Nella figura e rappresentato il nastro di una macchina che

• si trova nello stato q5;

• legge il simbolo 1 nella terza casella del nastro. La coppia costituita da uno stato e dal simbolo in lettura viene detta configurazione.

Il comportamento istantaneo della macchina è determinato dalla configurazione in cui si trova: in base a questo la macchina può:

• scrivere nella casella in lettura un altro segno, lasciare il segno trovato, oppure cancellarlo e lasciare la casella bianca;

• spostare la lettura sulla casella immediatamente a destra oppure sulla casella immediatamente a sinistra;

• cambiare stato.

Quello che la macchina deve fare viene stabilito da una tabella che fa corrispondere alle possibili configurazioni la terna di azioni da intraprendere.

Una volta prescritta la configurazione iniziale e approntato un nastro con eventualmente simboli scritti in alcune caselle, un’esecuzione consiste nel procedere attraverso la tabella delle istruzioni cercando la configurazione in cui ci si trova e obbedendo alle istruzioni, perciò scrivere nella casella in lettura, spostare la casella in lettura e passare a un nuovo stato. Ad esempio, la tabella di istruzioni per scrivere il numero 1/3 in notazione binaria su un nastro bianco con l’esecutore inizialmente nello stato q0, può essere la seguente:

Si noti che le prime due istruzioni fanno scrivere 0 e che le altre due istruzioni si ripetono alternate indefinitamente a produrre la parte rimanente (e infinita) della scrittura: 010101010…

Si noti anche che non vengono considerate configurazioni con caselle non bianche in lettura poiché si prevede che queste non saranno mai necessarie. Per eseguire le istruzioni di una macchina di Turing sono richieste solo attenzione, precisione e pazienza.

Nient'altro.

LA GUERRA A BLETCHLEY PARK

Ma la rilevanza storica di Alan Turing è legata in modo cruciale ad altri eventi di enorme importanza del secolo passato. Gli eventi storici che si susseguirono in quegli anni culminarono con lo scoppio della seconda guerra mondiale. Turing (che nel 1938 era Fellow di King’s College a Cambridge) venne arruolato, come molti altri eccellenti scienziati britannici, presso la Government Code and Cypher School, i servizi segreti inglesi di stanza a Bletchley Park. Il suo contributo fu quello di sviluppare nuovi metodi per decifrare i messaggi del nemico.

Alan Turing fu sicuramente uno dei più grandi eroi britannici, anche se il suo contributo per combattere il nemico del suo Paese è difficile da valutare con gli schemi usuali: non si distinse per particolari azioni avventurose, ma fu l’uomo che rese possibile conoscere le intenzioni del nemico in tempo reale. Grazie a quei metodi, dal giugno 1941 l’Alto Comando inglese era a conoscenza di tutte le comunicazioni tra le forze naziste e Winston Churchill riceveva ogni giorno una sintesi dei messaggi scambiati dalle forze nemiche. Le navi mercantili venivano informate delle possibili rotte degli U-boot; le forze terrestri conoscevano i movimenti delle forze nemiche; nei giorni precedenti il D-Day, gli alleati furono in grado di verificare l’efficacia delle notizie erronee che stavano lasciando circolare per distogliere l’attenzione dei nazisti dalle spiagge della Normadia.

La macchina Enigma

Il gruppo in cui lavorava Turing doveva decifrare i messaggi tedeschi codificati con il sistema Enigma. Il sistema Enigma, inventato nel 1918 dall’ingegnere tedesco A. Schrebius e modificato nei decenni successivi, era uno strumento ragionevolmente semplice da usare per scrivere e leggere messaggi in codice. Una macchina Enigma era contenuta in una scatola in legno delle dimensioni di una grossa scatola da scarpe e pesava circa 12kg. L’utilizzatore aveva a disposizione una tastiera alfabetica con cui comporre il messaggio; il messaggio in codice usciva, lateralmente, su una striscia di carta per essere trasmesso senza timore che intercettatori nemici potessero comprenderne il contenuto (si veda il riquadro La cifratura Enigma).

L’enorme comodita del sistema di codifica Enigma consisteva nel fatto che la decodifica di un messaggio avveniva mediante lo stesso strumento e con la medesima procedura: battendo il messaggio cifrato sulla tastiera si otteneva il messaggio “in chiaro” sulla striscia di carta. Questa notevole semplificazione di uso derivava dalla struttura interna dell’Enigma.

Per fortuna, i servizi segreti polacchi erano riusciti ad ottenere macchine Enigma funzionanti prima dello scoppio della guerra e, studiandone la struttura interna, Alan Turing lancio il suo attacco al codice con le armi della matematica astratta. Trovo che l'ingegnoso sistema presentava punti deboli, migliorando l’analisi al punto da rendere possibile ai servizi segreti inglesi di decodificare quasi ogni giorno il traffico radio del nemico. Oltre a sfruttare le proprietà matematiche, introdusse un sistema di valutazione probabilistica che permetteva di meccanizzare la ricerca del codice corretto: le configurazioni iniziali ricevevano voti che valutavano quanto potessero essere sospettate di essere quella giusta e la ricerca giornaliera si sviluppava seguendo la traccia del maggior sospetto.

La cifratura Enigma

La cifratura prodotta dall’Enigma era un'evoluzione del metodo di cifratura detto “di Giulio Cesare” perche era stato il condottiero romano ad introdurlo per comunicare in segreto con i suoi generali. Si adotta una permutazione delle lettere dell’alfabeto, ad esempio al posto di una lettera si scrive quella che la segue di tre posti nell’ordine alfabetico. La parola “EFFETTO” verrebbe trasmessa come “HIIHZZR”. A prima vista, la lettura della parola cifrata scoraggia i curiosi che desiderano sapere che cosa Cesare stia trasmettendo ma non conoscono il metodo adottato da Cesare. Pero, analizzando con calma la parola, si notano caratteristiche peculiari: ci sono due gruppi di coppie di lettere uguali. In italiano questo accade rarissimamente per vocali, ma molto spesso per consonanti. Dunque, e plausibile pensare che “I” e “Z” siano codici per consonanti distinte. Sotto questa ipotesi, e necessario che “H” sia il codice di una vocale e pure “R” e molto probabile che sia una vocale distinta dalla precedente. Con queste considerazioni a disposizione, tentare di indovinare la parola diventa ragionevole: oltre alla parola “EFFETTO” che ha effettivamente generato il codice, vi sono altre possibili soluzioni sensate

ABBASSI ABBASSO ABBATTE ABBATTI ABBATTO

ACCADDE AFFACCI AFFANNO AFFATTO ALLACCI

ALLATTI ALLATTO AMMACCO AMMASSI AMMASSO

AMMAZZI AMMAZZO ANNAFFI APPANNI APPANNO

ARRABBI ARRAFFI ARRAFFO ASSAGGI ATTACCO

AZZANNI AZZANNO ECCELLA ECCELLI ECCESSI

ECCESSO ECCETTO EFFETTI EFFETTO IMMILLA

Ma, ci sono altre due considerazioni che le riducono drasticamente. Il codice di Cesare sposta ogni lettera con lo stesso passo: “H” e il codice di una vocale e “I” e il codice della consonante che segue quella vocale in ordine alfabetico.

Inoltre, le vocali codificate da “H” e “R” distano tra loro esattamente quanto le lettere che le codificano, cioé ci sono sette lettere nell’ordine alfabetico tra le due vocali. Le due vocali possono essere soltanto

• “A” (codificata da “H”) e “I” (codificata da “R”); in questo caso “I” e il codice di “B” e “Z” e il codice di “P”. Ma la parola “ABBAPPI” non esiste in italiano.

• “E” (codificata da “H”) e “O” (codificata da “R”); in questo caso “I” e il codice di “F” e “Z” e il codice di “T”. E la parola “EFFETTO” esiste in italiano.

Per evitare che un attacco per decifrare il messaggio abbia un tale successo, si può pensare di usare una permutazione meno “strutturata” di quella di Cesare, ma la prima parte dell’analisi precedente rimane valida: le lettere uguali vicine sono codici per consonanti distinte e si capisce che codici sono stati assegnati a vocali. L’elenco delle possibilità certo non si riduce a un’unica soluzione, ma in un testo di più di una parola si troveranno altri indizi che permetteranno di risalire alla permutazione.

Le macchine Enigma contenevano un meccanismo che preveniva un tale attacco: una pressione di un tasto sulla tastiera, oltre a scrivere il codice, produceva una diversa permutazione delle lettere: premendo un tasto sulla tastiera l’operatore, oltre a ottenere il codice corrispondente alla lettera sul tasto che aveva premuto, mandava un segnale che produceva una modifica della permutazione. Cosi la prossima lettera nella parola viene codificata con una permutazione completamente diversa dalla precedente.

DOPO LA GUERRA: LE MACCHINE PENSANTI

Negli anni successivi alla seconda guerra mondiale, laboratori di ricerca inglesi e americani iniziarono una sorta di competizione nella realizzazione di quelli che sarebbero stati i primi calcolatori. Molti degli scienziati che avevano lavorato a progetti scientifici di carattere bellico durante il periodo di guerra, progettando e realizzando macchine per calcoli automatici, mettevano ora a frutto in tempo di pace le loro esperienze belliche. Alan Turing collaboro con laboratori inglesi, prima a Londra, poi a Manchester, e durante questo periodo affronto anche un problema, principalmente di carattere etico e filosofico, piuttosto che tecnico.

Considero il problema di porre in modo corretto la domanda “le macchine possono pensare?” Nell’articolo “Computing Machinery and Intelligence”, pubblicato nel 1950 sulla rivista Mind, Alan Turing propone di considerare la domanda: “Le macchine possono pensare?” Questo dovrebbe iniziare con le definizioni del significato dei termini “macchina” e “pensare”. Le definizioni potrebbero essere studiate in modo da riflettere il più possibile l’uso comune delle parole, ma un tale metodo è pericoloso. Se si dovesse trovare il significato delle parole “macchina” e “pensare” esaminando come vengono usati normalmente sarebbe difficile evitare la conclusione che il significato e la risposta alla domanda “Le macchine possono pensare?” verranno trovati mediante un sondaggio d'opinione. Ma questo è insensato.

Da buon matematico, sa come affrontare il problema di definire un concetto “intuitivamente ovvio”; dopo tutto nel 1937 aveva capito che era necessario definire quell’altro concetto “intuitivamente ovvio” di metodo meccanico per risolvere il problema proposto da David Hilbert (non l’avesse fatto, oggi non ci sarebbero i computer…).

In effetti, Alan Turing, avendo introdotto una nozione astratta di “macchina” che si stava rivelando estremamente precisa ed efficace, non ha problemi a spiegare in che senso si può interpretare il termine “macchina”. Per quanto riguarda invece il problema di definire il termine “pensare”, evita completamente una definizione astratta del concetto, ma prosegue dicendo che: Invece di provare a dare una tale definizione, sostituirò la domanda con un'altra, che è strettamente connessa a quella e che si esprime in termini relativamente non ambigui. Si può descrivere la nuova forma della domanda in termini di un gioco che chiamiamo il “gioco d’imitazione”. […] Si gioca in tre: un uomo (A), una donna (B) e un interrogatore (C) che può essere di sesso qualunque. L’interrogatore è in una stanza, separato dagli altri due. Lo scopo del gioco per l’interrogatore è quello di determinare chi sia l’uomo e chi la donna. Li conosce come X e Y e alla fine del gioco deve dire che “X è A e Y è B" oppure che “X è B e Y è A”. L’interrogatore può fare domande ad A e B di qualunque genere. […] Lo scopo di A nel gioco è di far in modo che C sbagli le identificazioni […] Lo scopo di B nel gioco è di aiutare l'interrogatore. La migliore strategia per B è probabilmente di dare risposte vere. “Che cosa succede quando una macchina prende il posto di A nel gioco?” Le identificazioni errate dell’interrogatore saranno tante quante quelle fatte nel gioco con un uomo e una donna? Queste domande sostituiscono la domanda originale “Le macchine possono pensare?”

Turing non risponde alla domanda. Intende soltanto porre una questione, che stava sorgendo negli ambienti scientifici, in un modo che gli sembra scientificamente più corretto di quello che da per scontato il significato di “pensare”.

Poco tempo dopo, Alan Turing moriva ma le sue intuizioni hanno lasciato tracce significative nella società moderna. Il percorso che abbiamo tracciato attraverso alcune realizzazioni scientifiche di Alan Turing conduce ad analizzare alcuni momenti cruciali del pensiero scientifico del XX secolo. Molto di questo e rimasto sconosciuto al pubblico – vuoi perché Top Secret, vuoi perché altamente specialistico – ma le ricadute di quanto egli aveva ottenuto sono state enormi e tangibili per tutta l’umanità. E stata una personalità scientifica di enorme valore, un genio che ha segnato momenti storici, filosofici e scientifici importantissimi e che, soltanto ora, inizia ad essere apprezzato.

BIBLIOGRAFIA

• Andrew Hodges. Alan Turing, Una biografia. Universale Bollati Boringhieri. 2006, pp. 762

• Roberto Lucchetti, Giuseppe Rosolini. Matematici al bar. FrancoAngeli, 2012.

pp. 162

Approfondimenti (a cura della redazione)

• http://www.turing.org.uk/: sito web gestito da Andrew Hodges

• Hugh Whitemore. Breaking the code (testo teatrale dal quale e stato tratto uno sceneggiato televisivo; il testo e stato rappresentato al Festival della Scienza di Genova ma mai distribuito in Italia, come lo sceneggiato)

• http://www.turingarchive.org/: archivio digitale di tutto il materiale prodotto da Turing. Si possono trovare sia documenti personali sia le copie dei manoscritti originali del suoi articoli.

• Yurij Castelfranchi, Oliviero Stock, Macchine come noi. La scommessa dell'intelligenza artificiale, Laterza, 2003, Bari. pp. 285